(CS285) Lecture 9 - Advanced Policy Gradients
28 Dec 2023이 글은 UC Berkeley 의 교수, Sergey Levine 의 심층 강화 학습 (Deep Reinforcement Learning) 강의인 CS285를 듣고 작성한 글 입니다.
Lecture 9의 강의 영상과 자료는 아래에서 확인하실 수 있습니다.
- Fall 2020 ver.
+추가) 아래의 lecture slides들을 추가로 참고하였습니다.
- Natural Policy Gradients, TRPO, PPO from John Schulman
- Natural PG, PPO, TRPO from from Katerina Fragkiadaki
< 목차 >
Lecture 9 의 주제는 Advanced Policy Gradient입니다.
Lecture 6까지 다뤘던 policy-based algorithm 으로 회귀했습니다.
 Slide. 1.
Slide. 1.
Goal of This Lecture
이번 lecture는 수학적인 얘기가 많아서 직관적이지 않고 꽤 어렵울 수 있습니다. 그래서 이번에는 본 lecture의 motivation, goal과 summary에 대해 먼저 얘기해보고자 합니다.
앞선 lecture 4,5,6 에서는 policy-based methods들의 발전사를 다뤘습니다.
그리고 이들 모두가 공통된 goal을 target 하고 있었음을 기억해야 하는데,
이들은 다음과 같습니다.
- 1.학습이 Unstable 하다
- Gradient의 Variance가 너무 크다
- Optimization Step Size를 제대로 정하기 어렵다.
- 2.좋은 Policy를 만들어내기 위해서는 너무나 많은 Sample이 필요하다 (즉, Sample Efficiency가 나쁘다)
여기서 variance가 크다는 문제는 baseline을 도입하고 critic을 사용하는 등의 해결책으로 어느정도 완화됐습니다 (여기까지가 lecture 6). 이번 lecture에서도 결국 원하는 것은 더 stable한 algorithm을 얻는 것입니다. 오늘 lecutre의 idea가 집약된, policy based 로 문제를 풀 경우 우리가 시도해볼 수 있는 방법 중 가장 단순하면서도 강력한 Proximal Policy Optimization (PPO)의 1저자이자 OpenAI의 Research Scientist인 John Schulman의 seminal lecture에서도 PPO를 위한 build up을 위해 동일한 문제를 언급합니다.
 Fig. Source from John’s Lecture
Fig. Source from John’s Lecture
이 NPG, TRPO, PPO가 풀고자 하는 문제와 motivation은 모두 같은데,
바로 optimization 할 때 신뢰할만한 방향으로 (Trust Region 내에서) 최대한 보수적으로 한 step 크게 policy를 improvement하자는 것입니다.
다만 NPG에서 PPO로 갈수록 algorithm이 더 단순해지고 Deep Neural Network Architecture들과도 궁합이 잘 맞는, stable한 방법론으로 계속해서 진화를 했다고 생각할 수 있습니다.
- 2001, Kakade et al. Natural Policy Gradient (NPG)
- 2015, John Schulman et al. Trust Region Policy Optimization (TRPO)
- 2017, John Schulman et al. Proximal Policy Optimization (PPO)
 Fig. Source from John’s Lecture. 2017년 까지의 policy-based method의 timeline
Fig. Source from John’s Lecture. 2017년 까지의 policy-based method의 timeline
이 lecture에서 Sergey가 유도하고자 하는 것도 결국 같습니다. 바로 아래 figure의 마지막 결론에 도달하는 것입니다.
 Fig.
Fig.
Policy gradient은 왜 working 하는가? 단순 Gradient Descent 인데? 만약 아니라면 어떤 조건이 있어야 improvement가 보장이 되는 걸까? 이 lecture는 증명의 연속입니다. 그리고 이 증명을 바탕으로 최종적으로 NPG, TRPO라는 algorithm을 도출해내는 것이 이 lecture에서 할 일입니다.
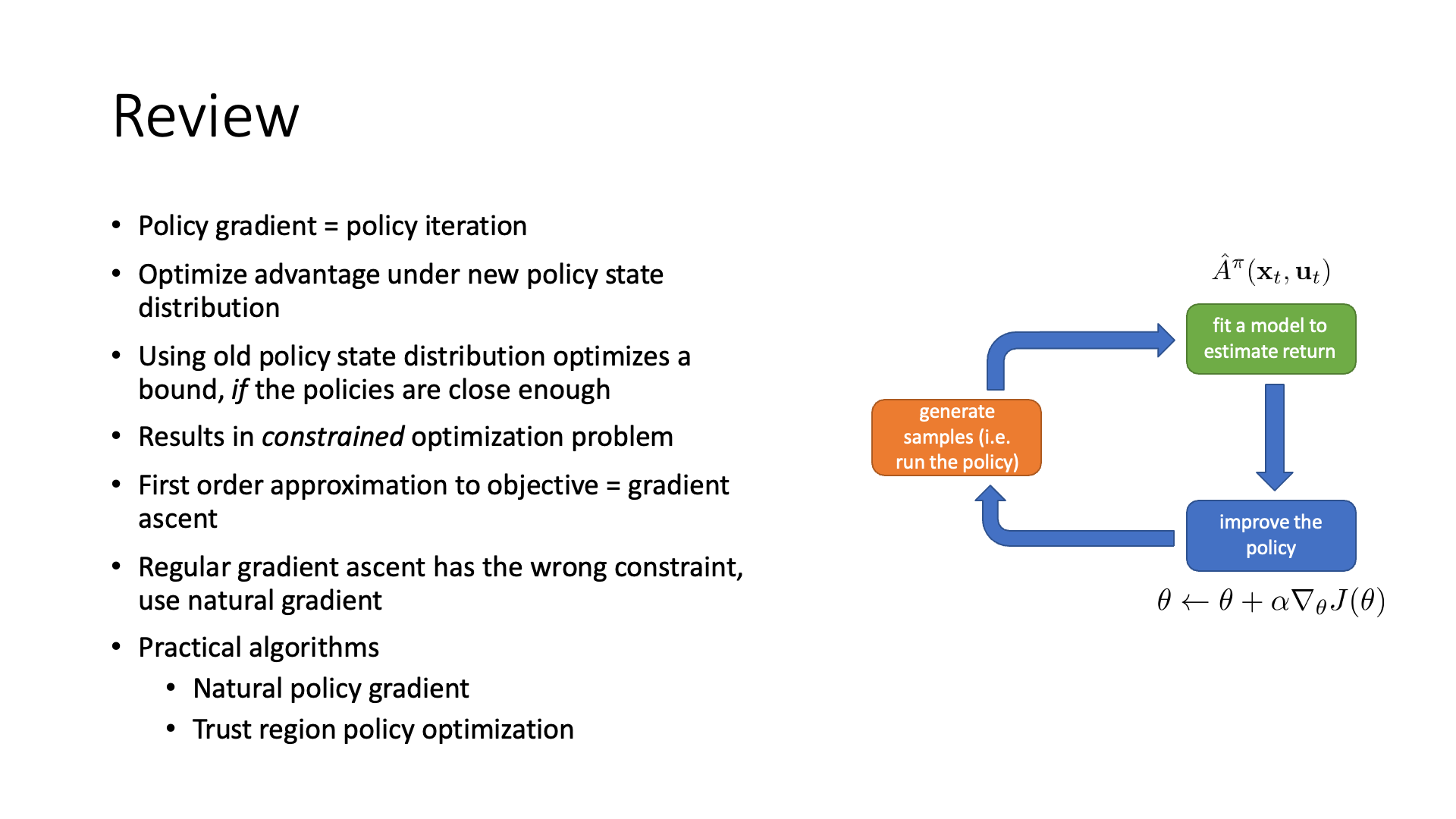 Fig.
Fig.
Review slide에 적혀있듯 우리가 밟게 될 증명과정은 다음과 같습니다.
- Policy gradient은 왜 working 하는가? (단순 Gradient Descent form이라서?)
- 사실 policy gradient = policy iteration 라고 할 수 있음.
- Policy iteration은 현재 policy로 평가한 Advatnage 값을 기반으로 policy를 update 할 경우 policy가 개선이 된다는 것이 보장되어 있음.
- 그렇다면 어떤 조건 하에서 policy improvement가 보장이 될까?
- 결국 어떤 제한된 조건의 최적화 (constraind optimization) 문제를 풀 것인데
- 이것이 NPG, TRPO이다.
- (본 lecture에서 PPO는 다루지 않았음)
Policy gradient가 policy iteration과 연관이 있다는 것이 지금은 와닿지 않을 수 있습니다. TRPO, PPO의 저자인 John Schulman의 seminar에 나와있는 comment를 보면 우리가 최적화할 (policy graident의) Loss에 어떤 조건을 넣어 최적화를 하느냐에 따라서 우리는 polciy iteration, policy gradient, natural gradient 중 한가지를 하게 된다는 것을 알 수 있습니다. (사실상 모두 관련이 있는 것임)
 Fig. Source from John’s Lecture
Fig. Source from John’s Lecture
최대한 policy improvement가 보장되는 좋은 조건 (보수적인 조건)을 이해하는 것이 이번 lecture의 최종 goal이 되겠습니다. 이제 본격적으로 lecture를 review해보도록 하겠습니다.
Policy Gradient and Policy Iteration
(Recap은 생략하겠습니다)
Sergey는 왜 policy-based algorithm이 실제로 잘 되는지에 제대로 이해하는 것이 중요하다고 얘기합니다. 이것을 바탕으로 내가 직면한 problem에 맞는 더 좋은 algorithm을 생각해 낼 수 있을 거니까요. (Sergey가 TRPO의 2저자입니다)
 Slide. 3.
Slide. 3.
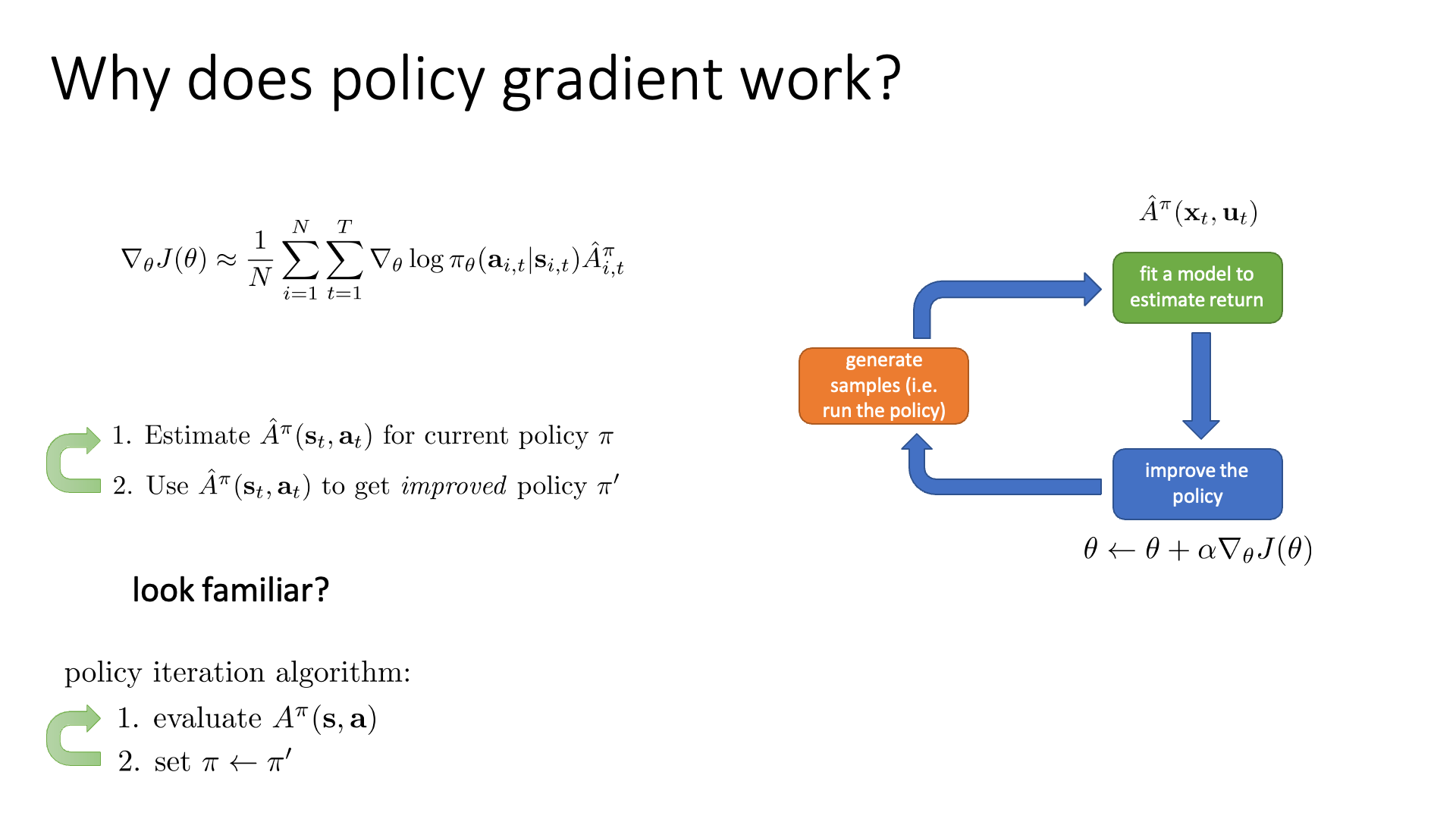
먼저 가장 단순한 형태의 policy gradient algorithm인 REINFORCE에 대해 다시 생각해 봅시다.
이는 현재 policy하의 action이 얼마나 그럴듯 했는가를 계산 (estimate) 하고 (Advantage Function, \(A^{\pi}(s,a)\) 계산),
이를 사용해서 policy를 한 step update 하죠.
Sergey는 이런 policy improvement의 mechanism이 lecture 7에서 배웠던 policy iteration과 유사하다고 얘기합니다.
- Actor-Critic Algorithm
- 1.Estimate \(\hat{A}^{\pi}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\) for current policy \(\pi\)
- 2.Use \(\hat{A}^{\pi}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\) to get improved policy \(\pi^{\prime}\)
- Policy Iteration Algorithm
- 1.evaluate \(A^{\pi}(\mathbf{s}, \mathbf{a})\)
- 2.set \(\pi \leftarrow \pi^{\prime}\)
두 algorithm에 차이가 있다면 policy 를 의미하는 network parameter를 direct로 최적화하느냐?
아니면 평가한 value를 기반으로 argmax 해서 이걸 policy로 쓰느냐? 였습니다.
Sergey는 이를 policy-based algorithm이 조금 더 gentle한 update를 한다고 표현하는데,
그 이유는 policy iteration은 argmax를 통해서 좋아보이는 행동에 과한 confidence를 주지만 policy-based algorithm은 좋아 보이는 (Advantage가 큰) 행동의 확률을 살짝 조정 (높혀) 하기 때문입니다.
좀 다르게 표현하면 policy gradient는 policy iteration의 soft버전이라고 할 수 있다고 합니다.
 Fig. Policy Iteration과 Policy Gradient는 상당히 유사하다고 할 수 있다. Advantage 값을 계산하고 이를 통해 policy를 개선하는 두 algorithms. Policy Iteration은 보통 argmax를 취해 각 state에서 optimal한 action을 할 확률이 1이고 나머진 0인 greedy policy를 사용하는 경우가 많지만 조금만 개선할 수도 있는 것 같다.
Fig. Policy Iteration과 Policy Gradient는 상당히 유사하다고 할 수 있다. Advantage 값을 계산하고 이를 통해 policy를 개선하는 두 algorithms. Policy Iteration은 보통 argmax를 취해 각 state에서 optimal한 action을 할 확률이 1이고 나머진 0인 greedy policy를 사용하는 경우가 많지만 조금만 개선할 수도 있는 것 같다.
Re-interpret Policy Gradient as Policy Iteration
Poliy Gradient (PG)와 Policy Iteration (PI)에 대해서 좀 더 명확히 해 봅시다. 우리가 해 볼 것은 REINFORCE같은 policy-based method를 policy iteration 으로 재해석 (re-interpret)하는 것 입니다. (어느정도 느낌은 왔겠지만 아예 수식적으로 그렇게 해 봅시다.)
 Slide. 4.
Slide. 4.
현재 policy (old policy or current policy)가 가지는 parameter가 \(\theta\)이고,
한 step update한 new policy의 parameter가 \(\theta'\)라고 할 때,
우리는 \(J(\theta')-J(\theta)\)에 대해 생각해 보려고 합니다.
이걸 증며하는게 무슨 의미를 가질지 생각해 보는것이 매우매우 중요합니다.
먼저 \(J(\theta)\)는 단지 모든 RL algorithm의 궁극적인 목적함수 \(J(\theta)\)입니다.
RL의 궁극적인 objective는 누적된 reward의 합 (cumulative reward)을 최대화 하는 것이었는데,
이를 trajectory distribution과 이런저런 trick을 써서 표현한 것이 바로 Vanilla Policy Gradient (VPG)의 Objective 였습니다.
누군가는 이를 Log Prob version의 PG Objective 라고 합니다.
Sergey가 말한 \(J(\theta')-J(\theta)\)라는 quantity가 의미하는 바는 정의에 따라서 parameter update를 한 step 함으로써 얼마나 정책에 improvement가 있었는가?를 나타내는 것이 됩니다.
당연하게도 이는 policy를 update함으로써 얼마나 받는 reward가 차이가 났는지?를 measure하는 것이기 때문입니다.
이제 우리가 해볼 것은 \(J(\theta')-J(\theta)\)라는 quantity를 어떤 특별한 기대값 형태로 표현해보는 것입니다.
어쩌면 당연해 보일 수 있는 수식이긴 한데 여기에 당연해보이지 않은 부분이 있으니, 바로 trajectory가 sampling될 trajectory distribution은 new policy의 parameter \(\theta'\)로 정의되어 있는데 반해 Advantage 값을 계산하는데 쓰이는 policy는 old policy, \(\pi_{\theta}\)로 정의되어있다는 겁니다.
이 수식을 우리가 유도하는 이유는 첫째로 이 수식이 policy iteration를 의미하기 때문입니다.
정말 그럴까요?
우리가 유도하고싶은 수식을 잘 봅시다.
\[\begin{aligned} & J(\theta') = J(\theta) + \mathbb{E}_{\tau \sim \color{red}{ p_{\theta'}(\tau)} } [ \sum_t \gamma^t A^{ \color{blue}{\pi_{\theta}} }(s_t,a_t) ] & \\ \end{aligned}\]Lecture 7의 tabular case에 대한 policy iteration은 현재 (old) policy를 사용해서 모든 \((s,a)\)에 대해서 value값을 측정하고 TD error를 사용해 A값을 계산 했었습니다. 그리고 위의 수식은 현재 step, \(\theta\)의 policy로 새로운 policy, \(\theta'\)가 만든 trajectory를 평가하는 걸 의미합니다. Trajectory distribution에 대해 기대값이 씌워져 있다는 것은 tabular case의 policy iteration이 모든 \((s,a)\)에 대해 A를 계산했던 것과 같은 일을 하는거죠. (물론 지금은 state space가 크기 때문에 당연히 sampling으로 바꾸겠지만)
그 다음 policy iteration은 모든 state, \(s\)마다 가능한 action들의 \(A(s,a)\)를 구했으니, 이 값이 가증 큰 action만 하도록 policy를 update 했습니다 (greedy, deterministic policy). 그리고 위의 수식 또한 모든 trajectory에 대해서 좋은 advantage를 받은 action들의 확률을 높혀주죠.
즉 두 algorithm의 mechanism은 거의 유사하다고 얘기할 수 있는데, 차이가 있다면 우리가 지금 증명하고자 하는 수식은 trajectory distribution이 새로운 policy, \(\theta'\)를 따른다는 겁니다. 이는 직관적으로 만약 policy가 좋은방향으로 update 됐다면 (improvement가 있었다면) new policy는 더 좋은 action에 더 높은 확률을 부여하고, 그 영향으로 agent가 더 좋은 state로 갈 확률도 증가하게 됩니다. 결과적으로 old policy가 이 새로운 trajectory를 평가할 때 더 높은 점수를 줄 것이고, 이것이 improvement가 얼만큼 있었는지를 measure하는 것이 되는거죠.
 Fig. TRPO에 있는 문단. notation이 조금 다르긴 하지만 주장하고자 하는 바는 policy iteration == policy gradient
Fig. TRPO에 있는 문단. notation이 조금 다르긴 하지만 주장하고자 하는 바는 policy iteration == policy gradient
TRPO에서는 이를 두고 ‘만약에 모든 state에 대해서 이 expected advatange 값이 non-negative라면 policy의 performance가 증가하는게 보장된다’라고 표현합니다. 혹은 모든 state에 대해서 0이면 수렴한 것 (constant)이 되겠죠. 만약에 policy가 deterministic하고 (or greedy; 즉 가장 Advantage가 큰 action에만 확률을 1 부여한다던가), advantage function을 근사 함수인 Critic network를 쓰는 것이 아니라, Dynamic Programming (DP)로 정확하게 계산한다고 하면 advantage value가 양수인 state-action pair가 단 하나라도 존재할 경우 개선됨이 보장된다고 합니다.
다만 general case에 대해서는 (Critic을 학습해서 advatantage function로 사용) error가 존재할 수 있기 때문에 실제로는 A값이 음수인데도 양수라고 한다거나 하는 가능성이 있어 언제나 policy improvement가 있지는 않을 수 있다고 합니다.
어쨌든 직관이 조금 필요하긴 한데, 우리는 위 수식을 통해서 policy gradient를 policy iteration처럼 해석할 수 있을 겁니다. 이제 이 수식을 유도해 봅시다.
먼저 \(J(\theta)\)는 sum of total reward임과 동시에, initial state distribution 하의 V(s_0)에 대한 기대값으로도 표현할 수 있었습니다.
(RL objecgive는 다양하게 표현할 수 있음을 lecture 4,5에서 배웠습니다)
그런데 위의 수식, \(\mathbb{E}_{s_0 \sim p(s_0)}[V^{\pi_{\theta}} (s_0)]\)에서 \(s_0\)가 sampling되는 부분은 policy에 영향을 받지 않는다는 것을 알 수 있습니다. 이 부분이 중요한 이유는 바로 이 기대값에 들어가는 distribution을 initial state에 대한 marginal이 \(p(s_0)\)이기만 하면 어떠한 trajectory distribution으로도 바꿀 수 있기 때문이라고 합니다. 다시 말해, inital state의 distribution \(p(s_0)\)만 같다면 그 뒤로는 trajectory의 distribution이 어떻게 되든 알 바아니기 때문에, \(p_{\theta} (\tau), p_{\theta'} (\tau), p_{\theta^{any}} (\tau)\) 무엇이든 사용할 수 있다는 겁니다. 여기서 \(\theta'\)의 trajectory distribution을 사용해서 나타내면 아래와 같은데,
\[J(\theta')-J(\theta) = J(\theta') - \mathbb{E}_{\tau \sim p_{\theta'}(\tau)}[V^{\pi_{\theta}}(s_0)]\]Sergey가 \(\theta'\)을 고른 이유는 우리가 궁극적으로 원하는 form이 \(p_{\theta'}(\tau)\)하의 기대값이기 때문이라고 합니다.
이렇게 해도 기대값 안의 수식은 \(V^{\pi_{\theta}}(s_0)\)로 \(s_0\)에만 의존하나 이 초기 상태는 같으므로 변하지 않습니다.
그 다음으로 이 수식은 어떠한 telescoping sum trick을 통해 또 아래와 같이 표현할 수 있는데,
(t=0부터와 t=1부터의 차이는 결국 \(V(s_0)\)라는 성질)
여기서 맨 마지막 수식에서 -가 +로 바뀌었다는 점에 주의하시고, 기대값에 있는 term을 보시면 Advantage Function과 비슷하게 생겼다는 걸 알 수 있습니다. 이제 아래처럼 수식을 끝까지 처리하면 우리가 원하는 바를 증명할 수 있습니다.
\[\begin{aligned} & J(\theta')-J(\theta) = \color{red}{ J(\theta') } + \mathbb{E}_{\tau \sim p_{\theta'}(\tau)}[\sum_{t=0}^{\infty}\gamma^t (\gamma V^{\pi_{\theta}}(s_{t+1}) - V^{\pi_{\theta}}(s_t) ) ] & \\ & = \color{red}{ \mathbb{E}_{\tau \sim p_{\theta'}(\tau)} [\sum_{t=0}^{\infty} \gamma^t r(s_t,a_t)] } + \mathbb{E}_{\tau \sim p_{\theta'}(\tau)}[\sum_{t=0}^{\infty}\gamma^t (\gamma V^{\pi_{\theta}}(s_{t+1}) - V^{\pi_{\theta}}(s_t) ) ] & \\ & = \mathbb{E}_{\tau \sim p_{\theta'}(\tau)} [\sum_{t=0}^{\infty} \gamma^t \color{blue}{( r(s_t,a_t) + \gamma V^{\pi_{\theta}}(s_{t+1}) - V^{\pi_{\theta}}(s_t) ) } ] & \\ & = \mathbb{E}_{\tau \sim p_{\theta'}(\tau)} [ \sum_t \color{blue}{ \gamma^t A^{\pi_{\theta}}(s_t,a_t) } ] & \\ \end{aligned}\]Applying Importance Sampling
우리는 이제 \(J(\theta')-J(\theta)\)라는 quantity를 표현하는 식을 얻게 되었습니다. 이를 잠시 \(A(\theta)\)라고 부르도록 하겠습니다.
 Slide. 5.
Slide. 5.
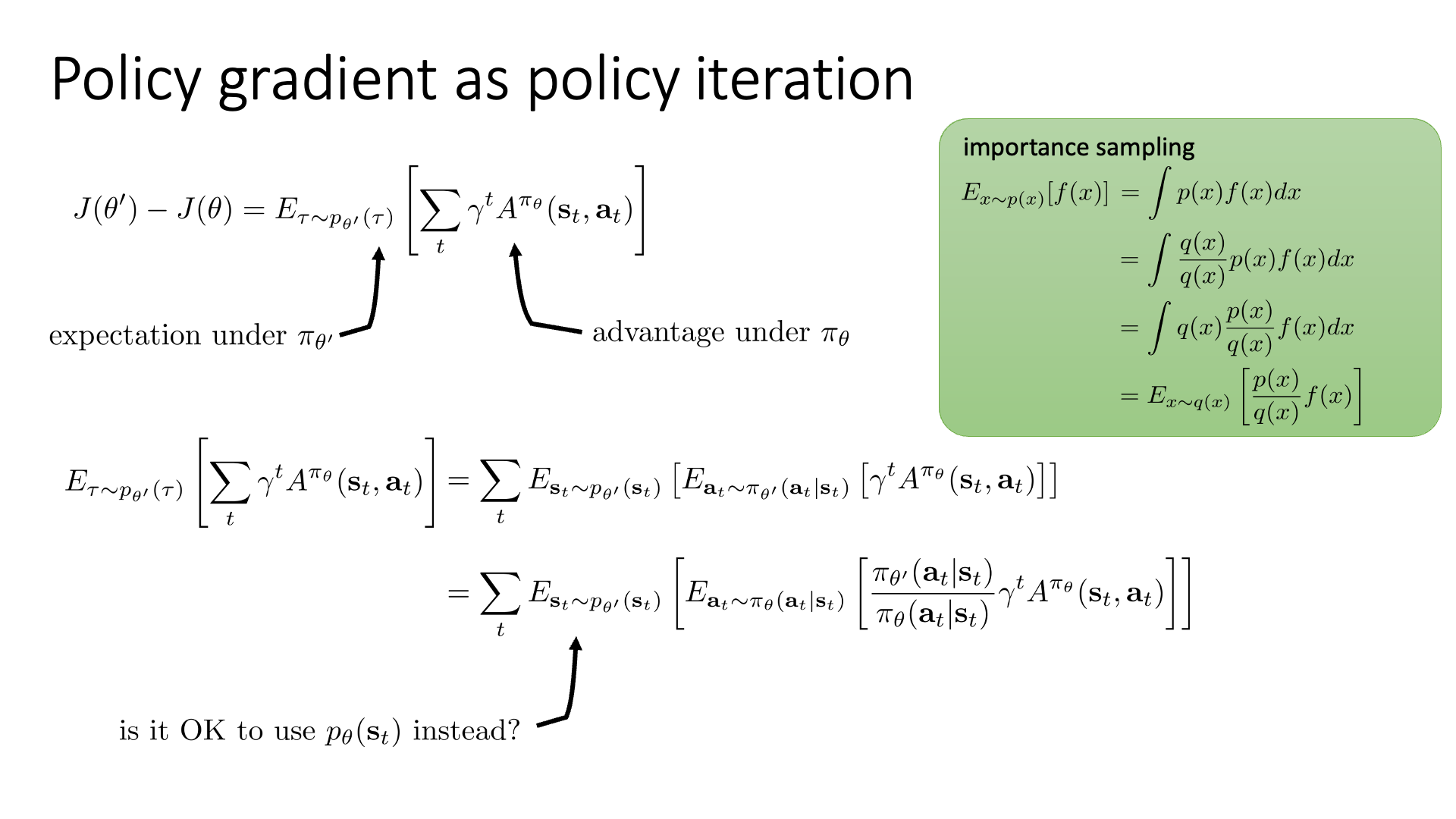
이제 \(A(\theta)\)을 증가시키면 improved policy를 얻을 수 있을텐데, 수식을 조금만 더 전개해 보겠습니다.
우선 Trajectory distribution을 state, action marginal로 바꿉시다. 왜냐하면 trajectory란 \((s_0, a_0, s_1, a_1, \cdots)\)의 연속이기 때문에 이를 decompose 할 수 있기 때문입니다. 그 다음 우리가 앞서 lecture 4, 5쯤에서 살짝 언급했던 Importance Sampling (IS)를 적용합니다.
\[\begin{aligned} & J(\theta')-J(\theta) = \color{red}{ \mathbb{E}_{\tau \sim p_{\theta'}(\tau)} } [ \sum_t \gamma^t A^{\pi_{\theta}}(s_t,a_t) ] & \\ & \qquad \qquad = \sum_t \color{red}{ \mathbb{E}_{s_t \sim p_{\pi_{\theta'}}(s_t)} [\mathbb{E}_{a_t \sim \pi_{\theta'} (a_t \vert s_t)} } [ \gamma^t A^{\pi_{\theta} (s_t,a_t)}] \color{red}{ ] } & \\ \end{aligned}\]이는 원래와 다른 distribution 하에서의 sampling을 통해 기대값을 계산할 때 원래의 distribution과 새로 적용한 distribution의 비율 (importance weight) 곱해줘서 값을 보정해주는 역할을 합니다.
\[\begin{aligned} & \mathbb{E}_{\tau \sim p_{\theta'}(\tau)} [ \sum_t \gamma^t A^{\pi_{\theta}}(s_t,a_t) ] = \sum_t \mathbb{E}_{s_t \sim p_{\pi_{\theta'}}(s_t)} [ \mathbb{E}_{a_t \sim \pi_{\theta'} (a_t \vert s_t)} [\gamma^t A^{\pi_{\theta}} (s_t,a_t)] ] & \\ & \qquad \qquad = \sum_t \mathbb{E}_{s_t \sim p_{\pi_{\theta'}}(s_t)} [ \mathbb{E}_{ \color{blue}{ a_t \sim \pi_{\theta} (a_t \vert s_t)} } [ \frac{ \pi_{\theta'} (a_t \vert s_t) }{ \color{blue}{ \pi_{\theta} (a_t \vert s_t) } } \gamma^t A^{\pi_{\theta} }(s_t,a_t) ] ] & \\ \end{aligned}\]이제 수식이 앞서 우리가 봐왔던 VPG의 수식과 굉장히 비슷해졌습니다. 우리가 VPG에서 썼던 gradient는 실제로는 아래의 loss를 미분해서 구한 것인데, (우리가 구하려는 gradient의 미분 전 형태 = Loss, \(L^{PG}(\theta)\))
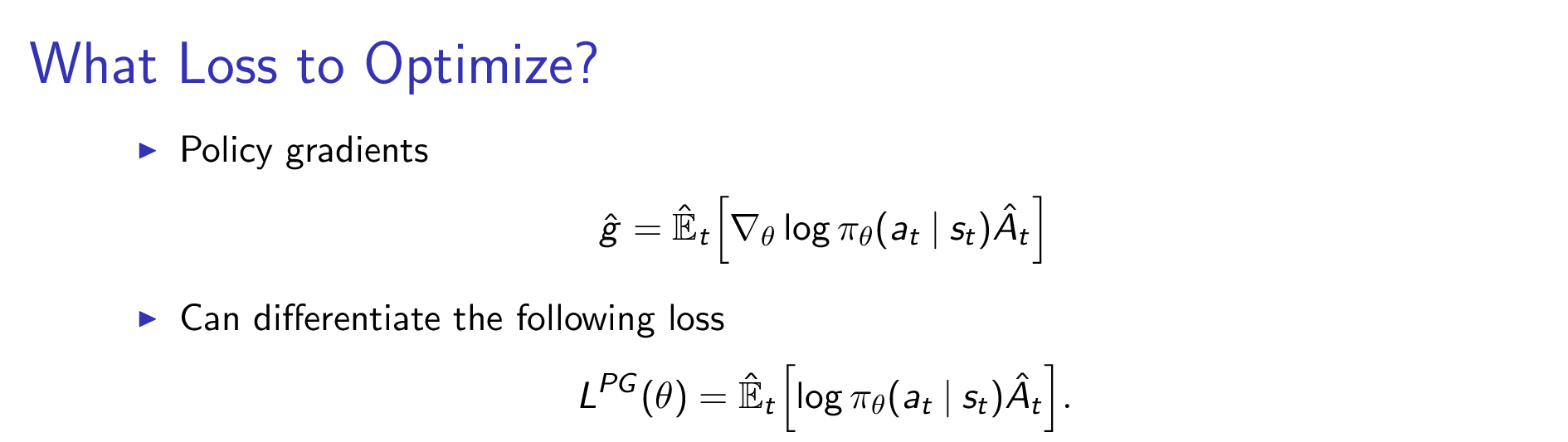 Fig.
Fig.
IS version도 \(\theta'=\theta\)인 지점에 대해서 미분값을 구할 경우 chain rule에 의해서 정확히 Log Prob version과 같은 값을 얻을 수 있습니다.
 Fig.
Fig.
그러면 지금의 수식을 써서 PG를 하면 (optimization을 하면) 되는데, 중요한 것은 우리가 \(\theta'\)이 무엇인지 모른다는 겁니다. 정확히는 \(\theta' = \theta\)인 지점에서의 optimization이 아니라면 계산할 수 없는것이죠.
이 \(\theta'\)는 update를 통해서 얻을 수 있는 다음 parameter 후보군 중 하나입니다. 이걸 모르기 때문에 우리는 \(p_{\theta'}(s_t)\)나 \(\pi_{\theta'}(a_t \vert s_t)\) 에서 state나 action을 sampling할 수 없습니다. Action을 sampling하는 부분 (기대값에 있는 distribution)은 IS를 적용해서 current policy \(\theta\)를 이용하기 때문에 괜찮아 졌습니다만 여전히 state distribution이 골칫거리입니다. 물론 우리가 실제로 한 step update를 해보고 그 policy로부터 sampling을 해볼 수는 있겠죠. 하지만 이는 별로 좋은 방법이 아닐겁니다.
 Slide. 6.
Slide. 6.
혹시 current policy를 따르는 \(p_{\theta}(s_t)\)에서 state sampling을 해볼 수 있을까요?
물론 distribution mismatch가 생기겠으나 일단 무시해 보는 겁니다.
일단 이 \(p(s_t)\)에 \(\theta'\)를 성공적으로 제거했다고 칩시다. 그러면 남은 \(\theta'\)는 importance weight의 분자에 들어가있는 \(\theta'\)뿐입니다. 더이상 \(\theta'\)로 부터 sampling 하지는 않기 때문에 이제 아무런 문제가 없습니다. 우리가 최종적으로 얻은 state distribution을 근사한 수식은 곧 \(J(\theta')-J(\theta)\)를 근사한 수식이 되는데, 이 quantity를 앞으로 \(\color{red}{ \bar{A}(\theta') }\)라고 쓰도록 합시다.
\[J(\theta') - J(\theta) \approx \bar{A} (\theta')\]이 \(\bar{A}\)를 이용하면 같은 trajectory에 대해서 expected return이 개선되므로 더 나은 policy를 얻는 것이 됩니다 (한 step update). 어떻게 얻을까요? 바로 \(\bar{A}\) \(\theta'\)를 최대로 하는 \(\theta'\)를 찾으면 됩니다.
\[\theta' \leftarrow \arg \max_{\theta'} \bar{A} (\theta)\]하지만 Sergey는 이게 사실일까요? 그리고 사실이라면 언제 사실일까요? (is it true? and when?)라는 질문을 던집니다.
왜냐하면 우리가 \(p_{\theta'}(s_t)\)를 \(p_{\theta}(s_t)\)로 바꿔서 \(A(\theta)\)를 \(\bar{A}(\theta)\)로 근사해버렸기 때문에 이에 대한 근거가 필요하기 때문이죠.
이것이 성립하기 위해서는 특정 제한 조건 (constraint) 이 필요한데,
바로 “\(\pi_{\theta}\)가 \(\pi_{\theta'}\)에 가까울 때 \(p_{\theta}(s_t)\)와 \(p_{\theta'}(s_t)\) 두 distribution이 충분히 가까워야 한다.”라는 조건입니다.
Bounding the Distribution Change
Why Do We Need Bound ?
이제부터 펼쳐질 내용들은 Natural Policy Gradient (NPG)를 제안한 Sham M. Kakade가 2002년 같은 해에 출판한 Approximately Optimal Approximate Reinforcement Learning의 내용과 TRPO의 유도를 따릅니다. 다음은 TRPO paper에 나온 한 구절입니다.
 Fig. Conservative Policy Iteration (CPI)는 \(\bar{A}(\theta')\)를 근사하는 것이 실제 policy improvement로 이어진다는 근거를 제시했지만 이를 generalize하지는 못했다.
Fig. Conservative Policy Iteration (CPI)는 \(\bar{A}(\theta')\)를 근사하는 것이 실제 policy improvement로 이어진다는 근거를 제시했지만 이를 generalize하지는 못했다.
Kakade et al.은 (수렴성에 대한) 어떤 문제를 해결 하기 위해서 Conservative Policy Iteration (CPI)를 제안했는데 이는 policy가 update될 때 이 update된 policy의 expected return가 얼만큼 증가했는지 (개선됐는지)? 에 대한 Explicit Lower Bound를 제공한다고 합니다.
(\(L\)은 \(\bar{A}(\theta')\)같은 approximation이고 \(\eta(\theta)\)는 expected return, \(J(\theta)\)임)
하지만 TRPO에서도 지적하듯 이는 모든 policy에 대해서 그런 것은 아니고 mixture policies에 대해서만 작동하기 때문에 general한 case에서 working하는 좋은 bound를 얻는 것이 이번 subsection의 목적입니다.
그런데 왜 Lower bound를 구해야 하는 걸까요?
ML에는 Expectation Maximization (EM)나 Variantional Inference의 Evidence Lower Bound (ELBO)같은 algorithm들이 있습니다.
이 두 algorithm은 완전히 같지는 않아도 비슷한 구석이 있는데,
예를 들어 log likelihood같은 objective function을 최대화하고 싶지만 log likelihood나 posterior 식을 완전히 유도하고 optimization하는 것이 사실상 불가능 하기 때문에 (너무 어렵기 때문에) 이들의 lower bound를 유도하고 이 bound를 높히는 것으로 learning objective를 우회한다는 공통점이 있습니다.
그렇게되면 log likelihood를 받치는 bound가 올라가면서 target하는 objective도 같이 올라가면서 자연스럽게 objective를 maximize하는 목표를 달성하게 됩니다.
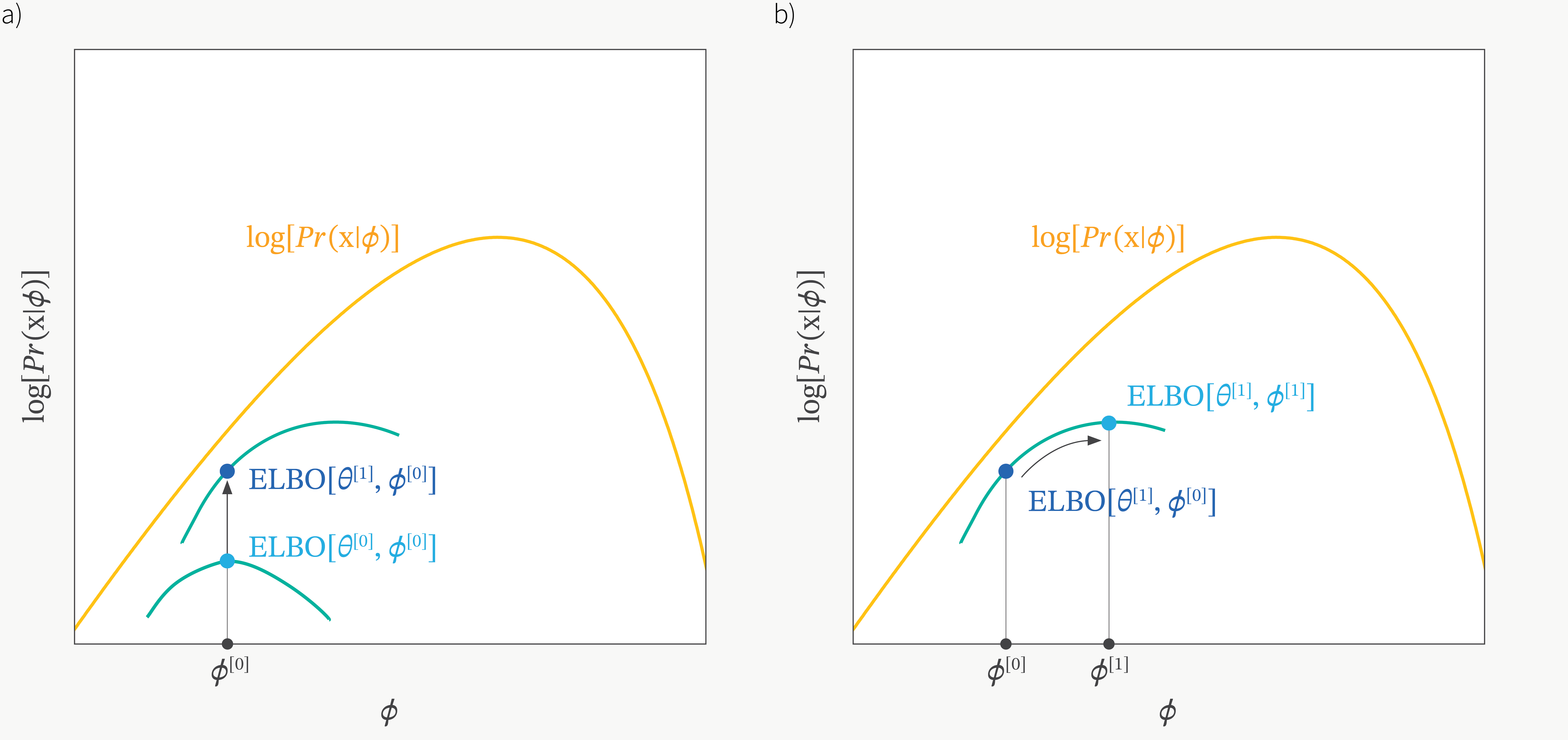 Fig. Illustration of Evidence Lower Bound (ELBO)
Fig. Illustration of Evidence Lower Bound (ELBO)
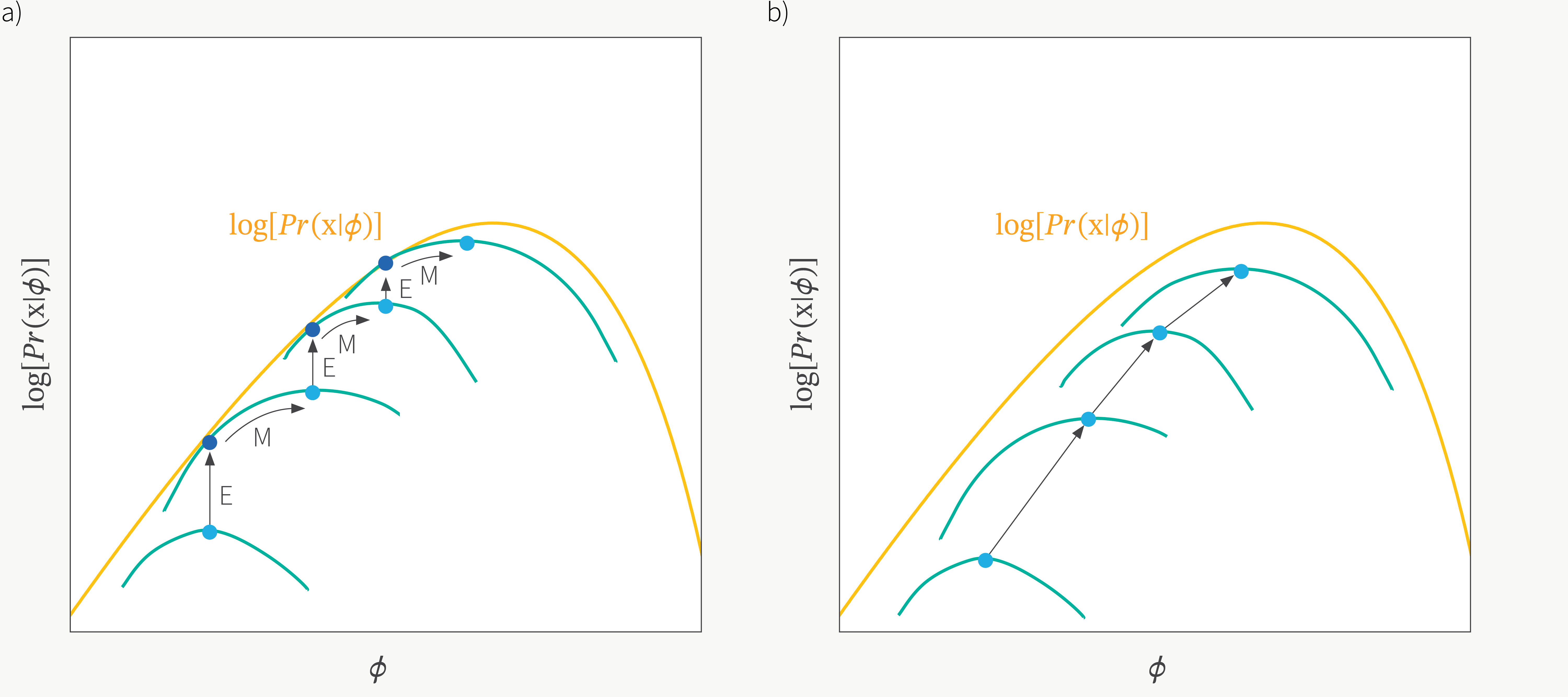 Fig. Illustration of Expectation Maximization
Fig. Illustration of Expectation Maximization
이 때 lower bound는 우리가 실제 구하고자 하는 true 값과 어느정도 괴리 (오차; error)가 있고, 실제로 이 error를 줄이는 step이 전체 optimization 과정에 포함될 수도 있고 아닐 수도 있습니다.
\[\text{objective} = \text{lower bound} \color{red}{+ \alpha}\]우리가 현재 처한 상황도 이와 비슷한데, 실제로는 \(A(\theta')\)를 계산하고 싶었으나 이를 근사한 \(\bar{A}(\theta')\)를 써야 합니다. 이제부터 논할 것은 이 quantity가 true값과 얼만큼의 오차 (error)가 있는지 입니다. 만약 어떤 제약 조건에서 이 error가 충분히 작다면 우리는 approximate objective를 optimize하는 것으로도 충분히 원하는 바를 달성할 수 있죠.
 Fig.
Fig.
결과적으로 TRPO에서는 위 figure에서 처럼 원래 objective function에 어떤 regularization term 을 추가한 것이 expected return을 의미하는 \(\eta (\theta)\)에 약간 못 미치는 bound를 형성하게 됩니다.
이 파란색 bound를 maximize하는 지점은 미분을 통해 간단하게 구할 수 있으니 bound 만 제대로 구하면 policy improvement를 쉽게 달성할 수 있게 되는데,
이 bound를 policy optimization의 lower (pessimistic) bound이라고 합니다.
이것이 염세적인 (pessimistic) bound인 이유는 실제로는 expected return이 더 높아질 여지가 있지만 ‘안 돼, 이정도로 충분해… 더 가면 망할거야’ 같은 느낌으로 update가 되기 때문이라고 비유할 수 있겠습니다.
Bounding the Distribution Change with Deterministic Policy
이제 bound를 실제로 구해봅시다.
먼저 policy parameter가 살짝 다르면 state distribution는 실제로 얼마나 차이나는가?를 measure하려고 합니다. 결론부터 말씀드리면 policy의 action distribution이 별로 큰 차이가 없다면 state distribution의 차이는 굉장히 작은 \(\color{red}{2 \epsilon T}\)로 bound가 됩니다. (\(\epsilon, T\)가 의미하는 바는 지금부터 설명드리겠습니다)
이를 증명하기 위해서 단순한 case부터 생각해 봅시다.
어떤 \(\theta\)로 parameter화 된 어떤 policy \(\pi_{\theta}\)이 deterministic하다고 가정합니다.
Deterministic이냐 stochastic이냐는 policy network가 return하는 것이 확률분포이냐 아니냐 라고 생각하시면 편합니다.
Deterministic policy의 경우에는 특정 state에서 무조건 어떤 action을 한다는 것이 결정되어 있는 것입니다.
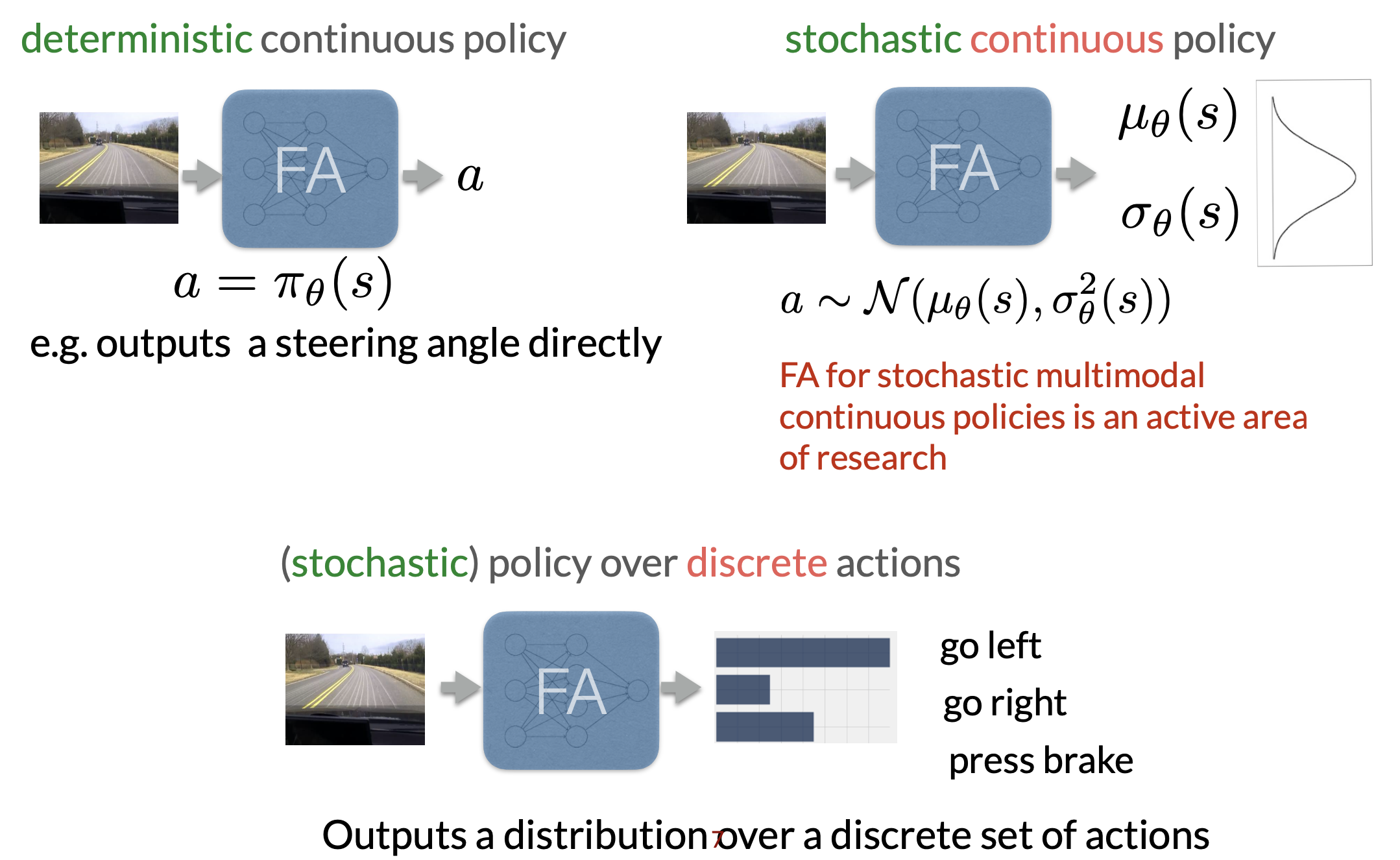 Fig.
Fig.
우리가 주장하고 싶은 것은 “\(\pi_{\theta}\)와 \(\pi_{\theta'}\)가 가까울 때 (비슷할 때) t번째 시점의 state distribution, \(p_{\theta}(s_t)\)와 \(p_{\theta'}(s_t)\)가 가깝다” 입니다. Policy가 deterministic하고 \(\pi_{\theta'}\) 가 \(\pi_{\theta}\)에 가깝다는건 다음의 조건을 만족할 경우라고 생각하겠습니다.
\[\pi_{\theta'} \text{ is close to } \pi_{\theta} \text{ if } \pi_{\theta'}(a_t \neq \pi_{\theta}(s_t) \vert s_t) \leq \epsilon\]즉 어떤 시점에서의 두 greedy policy의 action이 서로 다를 확률이 매우 작은 값, \(\epsilon\)이하라는 소립니다. 만약 2개의 action에 대해서 \(\pi_{\theta}\)는 \([0.51, 0.49]\)를 예측했는데 policy가 update되면서 \([0.49, 0.51]\)로 변하더라도 greedy이기 때문에 action이 바뀔 수 있는 것이죠.
앞서 lecture 2에서 Total Variation Divergence (TVD)를 계산해 봤던 것이 기억나실 겁니다. (외줄타기를 하는 example이 있었는데 기억이 안나시는분들은 lecture 2를 다시 보시길 추천드립니다)
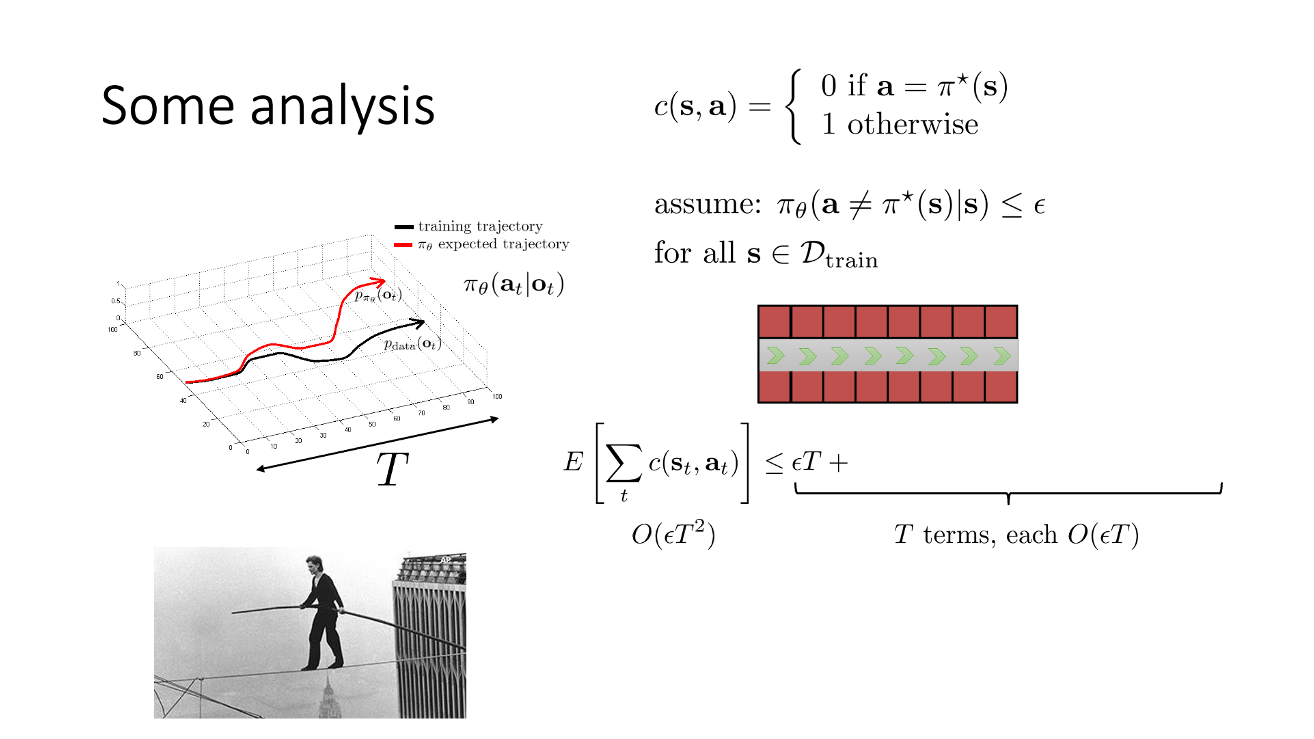 Fig. 외줄타기를 하는 example. 만약 매우 작은 epsilon의 확률로 정답과 다른 action을 하면 줄에서 떨어져 종료시점까지 penalty가 누적된다
Fig. 외줄타기를 하는 example. 만약 매우 작은 epsilon의 확률로 정답과 다른 action을 하면 줄에서 떨어져 종료시점까지 penalty가 누적된다
우리가 lecture 2에서 계산했던 것은 Behavior Cloning (BC)를 할 경우 정답과 다른 action을 함으로써 distributional shift가 일어날텐데, 과연 worst case의 경우 얼마나 큰 cost를 지불하게 될까? 였습니다. 즉 BC를 하는 경우의 bound를 계산하는 것이었죠. Trained policy가 완벽하지는 않을테니 training data와 다르게 행동할 가능성이 \(\epsilon\)만큼 생기고, trajectory가 진행될수록 (timestep이 증가할수록) 이것이 누적 됐었습니다.
 Slide. 9.
Slide. 9.
지금도 구하고자 하는것은 비슷합니다. Policy \(\theta'\)이 update 전 \(\theta\)와 다른 action을 할 확률이 \(\epsilon\)입니다. 시간이 흐를수록 error는 누적되어 다른 action을 하고 다른 state로 가고… 또 다른 action을 하고… 결국 trajectory가 상당히 많이 변하게 될것이며, t 시점에 agent가 어떤 state에 있을까?를 의미하는 state distribution도 크게 달라질겁니다. 즉 \(\theta'\)을 따랐을 때 어떤 \(t\) 시점의 \(s_t\)의 분포를 수식으로 나타내면 쓰면 다음과 같습니다.
\[p_{\theta'}(s_t) = (1-\epsilon)^t p_{\theta}(s_t) + (1- (1-\epsilon)^t) p_{\text{mistake}}(s_t)\]위의 수식은 두 가지 term으로 구성되어 있는데, 우변의 첫 번째 term은 \(s_t\)에 이르기 까지 모든 time-step의 state에서 같은 행동을 하는 경우로 updated policy, \(\pi_{\theta'}\) 가 정확히 current policy, \(\pi_{\theta}\)를 따라 가는것을 말합니다. Old policy, \(\theta\)와 new policy, \(\theta'\)가 정확히 똑같은 행동을 할 확률은 모든 timestep, state에 대해 \((1-\epsilon)\) 이므로 \((1-\epsilon)^t\)이 붙고 현재 timestep t에 대한 확률 \(p(s_t)\)만큼이 곱해지는 거죠.
두 번째 term은 앞서 말한 경우가 아닌 모든 경우를 얘기합니다. Lecture 2에서 처럼 이 state의 분포는 어떻게 생겼는지 모르지만 매우 복잡하다고 생각하고 이를 \(p_{mistake}\)라고 정의합니다.
이제 두 state distribution의 distance, 즉 TVD (혹은 \(D_{TV}\))를 계산해 봅시다.
\[\begin{aligned} & D_{TV} = \frac{1}{2} \sum_i \vert p_i - q_i \vert \\ & cf) D_{KL} = \sum_i p_i (\log p_i - \log q_i) \\ \end{aligned}\]Lecture 2에서 했던 것 처럼 \(A = A + (B - B)\)같은 항등식을 이용해 양 변에서 \(p_{\theta}(s_t)\)를 빼주고 절대값을 취해줍니다. 그리고 모든 확률 변수는 0~1사이의 값을 갖기 때문에 total variation divergence는 최대 2라는 값이 될 수 있는데, 이는 t시점에 존재하는 agent가 존재할 수 있는 모든 \(s_t\)중 \(p_{\theta'}(s_{t,1})\)값만 1일이고 나머지는 0이고, \(p_{\theta}(s_t)\)의 경우는 \(p_{\theta} (s_{t,2})\)만 1이고 나머지는 0이거나 하면 극단적으로 확률의 값 차이가 2가 되기 때문에 그렇습니다. (지금 수식 상으로는 \(1/2 \vert p_i - q_i \vert\)가 아니라 \(p_i - q_i\)라 2인듯 합니다.)
마지막으로 \(\epsilon \in [0,1]\)에 대해서 \((1-\epsilon)^t \geq 1 - \epsilon t\)가 성립하기 때문에 최종적으로 \(\vert p_{\theta'}(s_t) - p_{\theta}(s_t) \vert\)는 언제나 \(\color{red}{ 2\epsilon t }\) 값보다 같거나 작게 됩니다 (bound 됩니다).
Sergey는 이를 두고 it's not a great bound, but a bound라고 합니다.
아무리 커봐야 \(O(\epsilon T)\)보다 나빠질 일이 없고,
이는 timestep이 커질수록 state distribution이 달라지는 걸 어떻게 handling할 수는 없으나 만약에 우리가 policy의 차이인 \(\epsilon\)를 좀 더 빡세게 관리하게 되면 state marginal을 비슷하게 유지할 수 있다는 말이 됩니다.
Bounding with Stochastic Policy (General Case)
이번에는 lecture 2에서 했던 것 처럼 general case의 bound를 계산해봅시다. 어떤 임의의 (arbitrary) stochastic policy에 대해서 distribution change의 bound를 계산해 보는겁니다.
 Slide. 10.
Slide. 10.
이하 증명은 TRPO paper를 따르는데, general case에서는 아래의 경우를 두 policy가 비슷한 것으로 생각합니다.
\[\pi_{\theta'} \text{ is close to } \pi_{\theta} \text{ if } \vert \pi_{\theta'}(a_t \vert s_t) - \pi_{\theta}(a_t \vert s_t) \vert \leq \epsilon \text{ for all } s_t\]만약 두 policy의 TVD가 모든 state에 대해서 \(\epsilon\)으로 bound되어 있다면, 즉 모든 state, \(s_t\)에 대해서 policy의 distance가 \(\epsilon\)보다 작으면 두 policy는 비슷하고, 두 policy가 비슷하므로 state distribution이 매우 유사할 거라는 겁니다.
TRPO paper를 따라가다보면 결국 general case에 대해서도 \(2 \epsilon t\)의 bound가 형성됨을 알 수 있는데,
 Slide. 11.
Slide. 11.
결국 general case에 대해서도 두 policy의 모든 state에 대한 action distribution이 크게 차이가 나지 않으면 state distribution 이 크게 다르지 않음을 알 수 있습니다. (좀 놓쳤는데 paper를 참고해주시길 바랍니다)
\[\begin{aligned} & \pi_{\theta'} \text{ is close to } \pi_{\theta} \text{ if } \vert \pi_{\theta'}(a_t \vert s_t) - \pi_{\theta}(a_t \vert s_t) \vert \leq \epsilon \text{ for all } s_t & \\ & \vert p_{\theta'}(s_t) - p_{\theta}(s_t) \vert \leq 2 \epsilon t & \\ \end{aligned}\]이제 최종적으로 우리가 원하는 바를 증명해봅시다.
'과연 state distribution의 mismatch를 무시하고 A bar를 최적화 해도 policy improvement를 이뤄낼 수 있는가?'
먼저 new policy \(\pi_{\theta'}\)의 state distribution 하의 임의의 function에 대한 expectation을 아래와 같이 쓸 수 있죠.
여기에 \(\pi_{\theta}\)를 따르는 state distribution 하의 expectation을 뺀 quantity는 아래의 관계가 성립하는데,
\[\begin{aligned} & \sum_{s_t} p_{\theta'}(s_t) f(s_t) \geq \sum_{s_t} p_{\theta}(s_t) f(s_t) - \color{red}{ \vert p_{\theta'}(s_t) - p_{\theta}(s_t) \vert } \max_{s_t} f(s_t) & \\ \end{aligned}\]여기서 두 state distribution의 차이는 \(2\epsilon t\)로 bound되어 있기 때문에 아래와 같이 쓸 수 있습니다.
\[\begin{aligned} & \mathbb{E}_{p_{\theta'}(s_t)} [f(s_t)] \geq \mathbb{E}_{p_{\theta}(s_t)} [f(s_t)] - \color{red}{ 2 \epsilon t } \max_{s_t} f(s_t) & \\ \end{aligned}\]이제 이 임의의 함수를 importance sampling version의 policy optimization 수식으로 다시 바꾸면 우리는 아래와 같은 수식을 얻을 수 있습니다.
\[\begin{aligned} & \mathbb{E}_{ \color{red}{ p_{\theta'}(s_t) } } [ \mathbb{E}_{a_t \sim \pi_{\theta}(a_t \vert s_t)} [ \frac{\pi_{\theta'}(a_t \vert s_t)}{\pi_{\theta}(a_t \vert s_t)} \gamma^t A^{\pi_{\theta} (s_t,a_t) } ] ] & \\ & \geq \mathbb{E}_{ \color{blue}{ p_{\theta}(s_t) } } [ \mathbb{E}_{a_t \sim \pi_{\theta}(a_t \vert s_t)} [ \frac{\pi_{\theta'}(a_t \vert s_t)}{\pi_{\theta}(a_t \vert s_t)} \gamma^t A^{\pi_{\theta} (s_t,a_t) }] ] - \color{blue}{ \sum_t 2 \epsilon t C } & \\ \end{aligned}\]여기서 C는 constant인데, 의미하는 바는 매 time-step마다 얻을 수 있는 최대의 보상, \(r_{max}\)와 eposide의 길이 \(T\)의 곱입니다. Episode의 길이가 정해지지 않고 무한대인 infinite horizon case라면 discount factor가 곱해지기 때문에 결국 C는 \(O(T r_{max})\)이거나 \(O(\frac{r_{max}}{1-\gamma})\)가 된다고 합니다. (자세한 내용은 TRPO 참조)
Where Are We At?
중간정리를 해봅시다. 우리는 이제 아래의 사실까지 알게 되었습니다.
- Policy Gradient는 왜 잘되는가?
- 사실 Policy Gradient == Policy Iteration 이다.
- Policy Iteration 처럼 매 optimization step시 policy가 improve됨이 보장되려면 \(\bar{A}(\theta')\)을 maximize하는 \(\theta'\)을 찾아야 하는데, 이 objective는 approximation이 포함되어 있다.
- 이를 무시하고 optimize하기 위해선 “update하려는 policy가 현재 policy와 너무 다르지 않을 것”이라는 constraint가 필요하다.
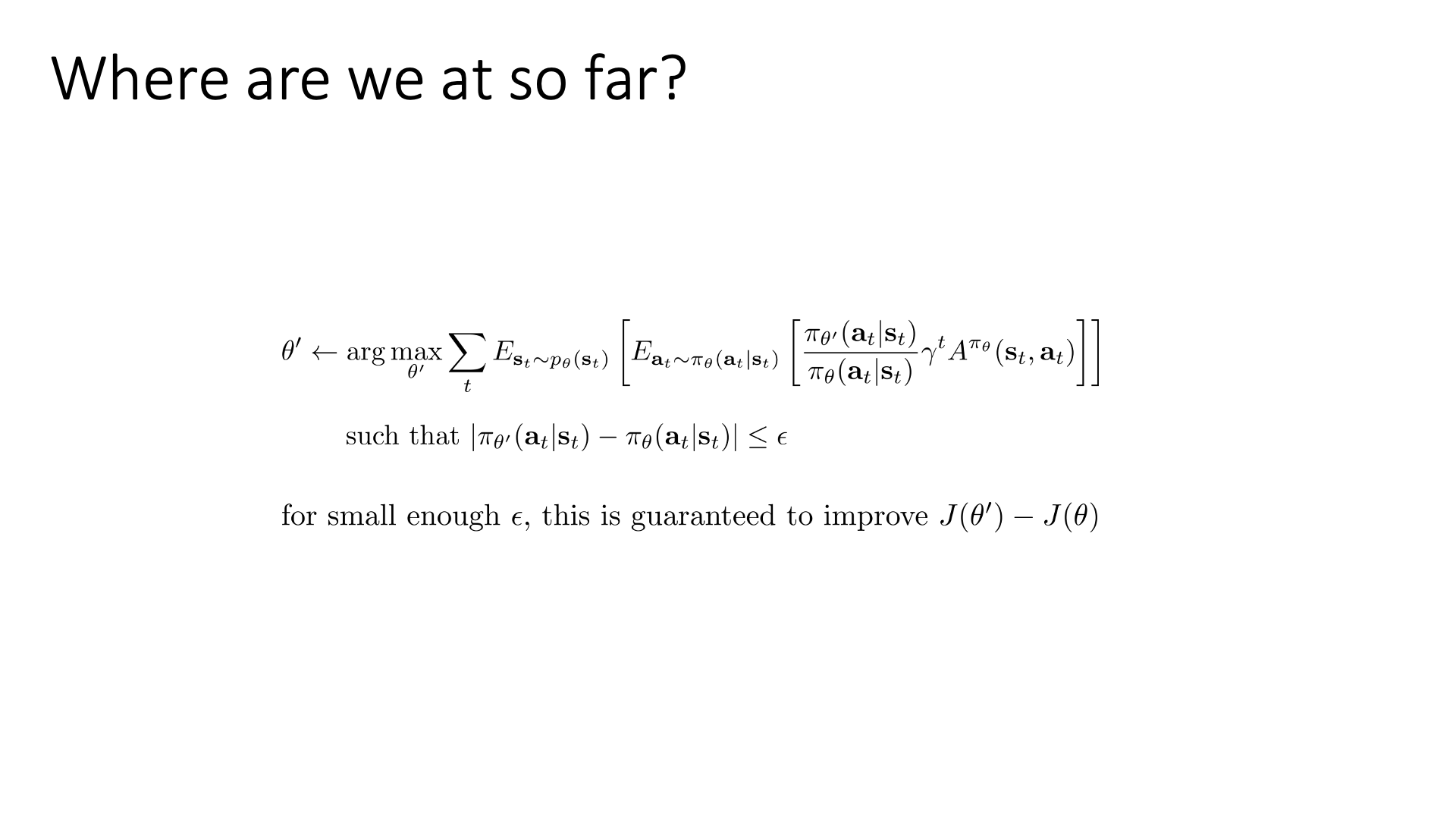 Slide. 12.
Slide. 12.
즉 두 policy의 divergence가 모든 state에 대해서 \(\epsilon\)보다 작다면 \(\bar{A}(\theta')\)를 maximize하는 것으로 policy improvement가 보장됩니다.
\[\begin{aligned} & \theta' \leftarrow \arg \max_{\theta'} \mathbb{E}_{s_t \sim p_{\theta}(s_t)} [ \mathbb{E}_{a_t \sim \pi_{\theta}(a_t \vert s_t)} [ \frac{\pi_{\theta'}(a_t \vert s_t)}{\pi_{\theta}(a_t \vert s_t)} \gamma^t A^{\pi_{\theta}} (s_t,a_t) ] ] & \\ & \quad \text{such that } \vert \pi_{\theta'}(a_t \vert s_t) - \pi_{\theta}(a_t \vert s_t) \vert \leq \epsilon & \\ \end{aligned}\]한 편, 앞서 언급했던 policy based method 의 main problem 들이 기억나실겁니다.
- 1.variance가 크다
- 2.optimization step size를 정하기 어렵다.
- 어떤 parameter는 policy가 변화하는데 큰 영향을 주는데 어떤 parameter는 그렇지 않다.
- 3.sample efficiency가 떨어진다.
 Fig. Source from John’s Lecture
Fig. Source from John’s Lecture
본격적으로 우리가 제한 조건이 있는 최적화 문제 (constraint problem)을 풀기 전에,
이런 일을 하는 이유는 step size를 정하기 어렵다와 sample efficiency가 떨어진다는 문제를 해결하기 위해서라는 걸 알고 상기하고 넘어가면 좋습니다.
곧 다룰 것이지만 VPG도 사실 constraint optimization으로 해석할 수는 있습니다.
그런데 이 constraint가 별로 nice하지 않았던게 문제였던 것이죠.
Importance sampling이 들어간 locally off-policy인 경우에는 더더욱 그렇습니다.
VPG의 (gradient descent를 하는 방법들 모두 포함) optimization은 사실 parameter space 상에서 반경 epsilon의 원 안에 존재하는 parameter set중 하느를 골라 그 것으로 paramter update를 한다라는 가정이 깔려있습니다.
즉 gradient descent를 하는 문제들은 현재 지점에서 반경 \(\epsilon\)내의 paramter중 가장 loss를 작게만드는 paramter를 골라야 하는데,
이것이 정확히 1차 미분을 한 direction으로 정해진 step size만큼 가는것과 같았습니다.
그런데 이 조건은 첫 번째로 모든 paramter가 policy에 끼치는 영향력이 같지는 않다는 점 (step size가 달라도 된다)과, state distribution을 무시한 경우에도 optimization을 할 수 있어야 한다는 데 있어 최적의 조건이 아닙니다. 1번이야 그렇다 치더라도 2번의 sate distribution을 조금 다른 걸 쓰겟다는 것은 off-policyness를 의미하는데, 실제로 \(\pi_{100}\)이 sampling한 trajectory를 가지고 \(\pi_{105}\)를 update하는 데 쓰고 재활용하기 위해서는 반드시 더 좋은 constraint이 필요하고, 그것이 우리가 얘기한 TVD가 \(\epsilon\)보다 작을 때를 얘기합니다.
Policy optimization method는 이렇듯 비슷한 objective여도 constraint가 어떤 것이냐에 따라서 다른 algorithm이 되기도 합니다 (behavior가 달라질 수 있습니다).
 Fig. Euclidean 제한조건을 주면 VPG, Policy distribution의 제한 조건을 주면 NPG, TRPO. Source from John’s Lecture
Fig. Euclidean 제한조건을 주면 VPG, Policy distribution의 제한 조건을 주면 NPG, TRPO. Source from John’s Lecture
Policy Gradients with Constraints (using Lagrangian Multiplier)
이제 어떻게 constraint optimization 문제를 풀 수 있는지 알아봅시다.
그런데 두 policy의 distance를 measure하는 것으로 TVD를 쓰는 건 별로 좋지 않은 선택일 수 있습니다. 왜냐하면 일반적으로 TVD는 어떤 확률 변수의 expectation으로 표현되지 않아 approximation하기가 힘들기 때문이라고 하는데, 그렇기 때문에 이보다 더 편리한 bound인 Kullback–Leibler Divergence (KLD)를 쓸것입니다.
 Slide. 14.
Slide. 14.
Sergey는 KLD를 사용하면 아래와같이 더 편리한 bound를 구할 수 있다고 합니다.
\[\begin{aligned} & \left|\pi_{\theta^{\prime}}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)-\pi_{\theta}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)\right| \leq \sqrt{\frac{1}{2} D_{\mathrm{KL}}\left(\pi_{\theta^{\prime}}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right) \| \pi_{\theta}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)\right)} \\ & D_{\mathrm{KL}}\left(p_{1}(x) \| p_{2}(x)\right) =E_{x \sim p_{1}(x)}\left[\log \frac{p_{1}(x)}{p_{2}(x)}\right] \\ \end{aligned}\]TVD와 KLD는 square root관계에 있으며, 말씀드린 것 처럼 KLD는 expectation (그리고 다시 sampling)으로 표현이 될 수 있습니다.
이제 우리는 KLD를 사용한 constrained objective를 풀게 되었습니다. 이 또한 error가 bound 되어 있기 때문에 policy improvement가 보장되는 optimization을 할 수 있을겁니다.
 Slide. 15.
Slide. 15.
Constraint optimization을 푸는 방법엔 여러가지가 있을 수 있으나, 단순한 방법 중 하나는 Lagrangian Multiplier을 사용하는 것이 있을겁니다.
\[\begin{aligned} & \mathcal{L}\left(\theta^{\prime}, \lambda\right) =\sum_{t} E_{\mathbf{s}_{t} \sim p_{\theta}\left(\mathbf{s}_{t}\right)}\left[E_{\mathbf{a}_{t} \sim \pi_{\theta}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)}\left[\frac{\pi_{\theta^{\prime}}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)}{\pi_{\theta}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)} \gamma^{t} A^{\pi \theta}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right]\right] & \\ & -\lambda\left(D_{\mathrm{KL}}\left(\pi_{\theta^{\prime}}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right) \| \pi_{\theta}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)\right)-\epsilon\right) & \\ \end{aligned}\] Slide. 16.
Slide. 16.
최적화를 하는 procedure는 이제 다음과 같습니다.
- 1.Maximize \(\mathcal{L}\left(\theta^{\prime}, \lambda\right)\) with respect to \(\theta^{\prime}\)
- 2.\(\lambda \leftarrow \lambda+\alpha\left(D_{\mathrm{KL}}\left(\pi_{\theta^{\prime}}\left(\mathbf{a}_{\ell} \mid \mathbf{s}_{t}\right) \| \pi_{\theta}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)\right)-\epsilon\right)\)
Primal variable, \(\theta\)에 대해서 최대화를 하고, Dual varialbe에 대해서 gradient descent step을 한스텝 취하는 겁니다.
직관적으로 Lagrangian Multiplier가 포함된 최적화 문제를 푸는 것은 constraint가 너무 크게 훼손(?, violated) 되면 \(\lambda\)를 키우고,
그 반대면 줄이는 방향으로 조절이 되면서 최적화를 진행하게 됩니다.
이런 방법으로 최적화를 하는 것을 Dual Gradient Descent라고 부르며 나중에 다른 chapter에서 더 detail하게 다룰 예정이라고 합니다.
아니면 이보다 더 heruistic한 방법을 사용할 수도 있다고 하는데, \(\lambda\)를 대충 설정하고 KLD term을 단지 원래 objective의 Regularizer로 보는 방법입니다.
직관적으로 생각해도 업데이트 될 정책이 이전 정책으로부터 꽤 멀리 가려고 하면 이를 잡아주는거니까 이렇게 해도 문제가 되지 않습니다.
그리고 1번의 Maximizing step도 실제로는 꽤 impractical 할 수 있으므로 gradient step 몇 번 하는걸로 대충 practial하게 처리할 수 있다고 합니다.
Natural Gradient
하지만 실제 TRPO paper에서 사용된 solution은 조금 다릅니다.
우리가 gradient descent를 하는 것 자체는 잘못되지 않았습니다.
다만 constraint가 잘못되었기 때문에 이를 수정해줄 것인데,
이를 잘 처리해주면 gradient에 어떤 term이 곱해져 policy가 improvement되는 direction으로 자연스러운 gradient (Natural Gradient)를 수정할 수 있습니다.
그대로 gradient descent를 하기만 하면 되죠.
어떻게 이게 가능할까요?
 Slide. 18.
Slide. 18.
우선 아래의 objective를 이전처럼 \(\bar{A}\) 라고 표기합시다.
\[\bar{A}(\theta') = \sum_{t} E_{\mathbf{s}_{t} \sim p_{\theta}\left(\mathbf{s}_{t}\right)}\left[E_{\mathbf{a}_{t} \sim \pi_{\theta}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)}\left[\frac{\pi_{\theta^{\prime}}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)}{\pi_{\theta}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)} \gamma^{t} A^{\pi_{\theta}}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right]\right]\]앞으로 조금 복잡해질 수 있는데, key idea는 다음과 같습니다.
- Objective에 대해서는 1차 근사를 (first order taylor approximation; linear)
- Constraint에 대해서는 2차 근사를 (secnod order taylor approximation; quadratic)
 Fig.
Fig.
Objective와 constraint를 분리해서 생각하고 합치는 것이 중요한데, 둘 다에 대해서 생각해보기 전에 먼저 objective에 대해서만 생각을 해 봅시다.
예를 들어 \(\bar{A}\)라는 objective function이 아래 figure의 blue curve라고 생각해 봅시다. 어떻게 해야 이 복잡한 곡선에서 한 step 갈 수 있을까요? 당연히 gradient descent를 아는 입장에서, 1차 미분을 한 뒤에 그 반대 방향으로 learning rate만큼 가면 될 텐데 좀 다르게 생각해 봅시다.
 Fig.
Fig.
우선 어떤 최적화 하려는 부분에 constraint이 걸려 있다고 생각해 봅시다. Red box로 표시되는 영역 (region)이 바로 constraint 입니다. 이 구간을 넘어가서는 안됩니다.
 Fig.
Fig.
이제 현재 parameter 지점에서 1차 미분 (gradient)를 구합니다 (green line). 이는 어떤 임의의 function을 현재 parameter point에 대해서 1st order taylor expansion한 것과 같습니다.
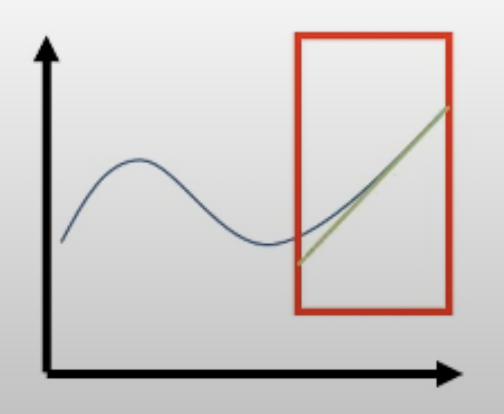 Fig.
Fig.
우리는 끝을 알수없는 loss surface가 정확히 어떻게 생겼는지는 모르지만,
현재 위치에서 taylor expansion (미분)을 통해 지역적으로나마 (locally) 이 function이 어떻게 알게된 겁니다.
하지만 직관적으로 blue curve 를 approximate 할 때 1차 approximate를 하는 것이므로 그 정해진 지점에서 많이 벗어나게되면 approximate function은 원래 function는 많이 다른 형태가 되어버리겠죠.
물론 2차 3차 근사를 하면 더 정확해지겠지만 그런 computational cost는 원하지 않습니다.
그런데 만약 우리가 신뢰할 만한 구간 (trust region)을 정해준다면 어떨까요?
우리는 이 region에서 objective를 최대화 (혹은 loss면 최소화)하는 parameter 하나를 pick하면 됩니다.
\[\theta' = \arg \max_{\theta'} \bar{A}(\theta')\]혹은 같은 얘기긴 하지만 내가 1차 미분을 해서 gradient를 얻었으니 gradient descent의 철학대로 gradient의 반대방향으로 가면 되는데, 이 때도 trust region을 벗어나지만 않으면 되겠습니다.
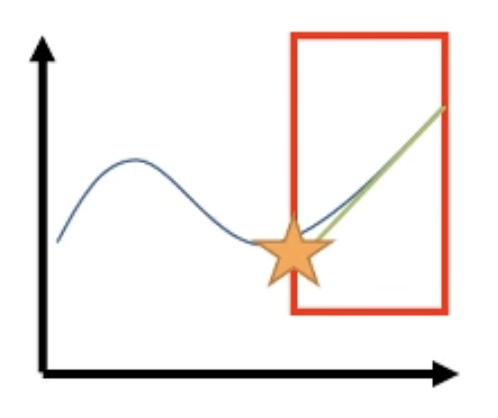 Fig.
Fig.
이 예시로 알 수 있는 것은 우리가 Objective를 1차 미분해서 gradient descent를 하려고 할 때 어떤 trust region이 잘 설정되어 있다면 optimization을 적절히 잘 할 수 있다는 겁니다. 이 trust region을 policy가 많이 변하지 않는 point들로 한정해서 설정하는 것이 우리가 하려는 optimization의 point입니다.
그럼 실제로 우리가 최적화 하고자 하는 objective, \(\bar{A}\)에 대해서 이 개념을 적용해 보도록 합시다.
 Slide. 19.
Slide. 19.
먼저 \(\bar{A}(\theta')\)를 1st order approximation 합니다. 여기서 좀 헷갈리시는 분들이 있을 수 있는데, 정확히 말하면 우리는 \(\theta'\)으로 아직 가보지는 않으니 모릅니다. 이것에 대해 미분하는 것은 어색하다는 생각이 들 수 있죠. 정확히는 현재 paramter, \(\theta\)에서 어떤 direction, \(d\)로 step size, \(\alpha\)만큼 움직일 것이고 \(d, \alpha\)를 search 하려는 겁니다. 즉 \(\theta' = \theta + \alpha d\)인 것이고 우리는 \(d \arg \max_d \bar{A} (\theta + \alpha d)\)를 실제로 하는 겁니다. 그리고 우리는 이 direction, \(d\)를 gradient descent처럼 구할 것이니 실제로 objective에 대해서 우리가 할 것은 1차 미분 밖에 없긴 합니다.
다시, 앞서 IS version의 PG인 \(\bar{A}\)를 \(\theta'=\theta\)인 지점에 대해서 미분하면 정확히 VPG와 같다고 말씀드렸습니다.
\[\begin{aligned} &\nabla_{ \color{blue}{ \theta^{\prime} } } \bar{A}\left( \color{blue}{ \theta^{\prime} } \right) =\sum_{t} E_{\mathbf{s}_{t} \sim p_{\theta}\left(\mathbf{s}_{t}\right)}\left[E_{\mathbf{a}_{t} \sim \pi_{\theta}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)}\left[\frac{ \color{blue}{ \pi_{\theta^{\prime}}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right) } }{\pi_{\theta}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)} \gamma^{t} \nabla_{\theta^{\prime}} \log \pi_{\theta^{\prime}}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right) A^{\pi_{\theta}}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right]\right]\\ &\nabla_{ \color{red}{ \theta } } \bar{A}( \color{red}{ \theta } ) = \sum_{t} E_{\mathbf{s}_{t} \sim p_{\theta}\left(\mathbf{s}_{t}\right)}\left[E_{\mathbf{a}_{\mathbf{t}} \sim \pi_{\theta}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)}\left[\gamma^{t} \cdot \color{red}{1} \cdot \nabla_{\theta} \log \pi_{\theta}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right) A^{\pi_{\theta}}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right]\right]=\nabla_{\theta} J(\theta) \end{aligned}\]여기서 “아니 그러면 결국 미분했을 때 VPG랑 같은데 왜 굳이 유도한거지?”라는 생각이 들 수 있는데, 이는 나중에 지역적으로 (locally) off-policy로 발전시키기 위해 다시 언급이 될겁니다. 왜냐면 \(\theta' = \theta\)가 아닌 point에서 미분하면 VPG와 달라지거든요.
그렇다면 여기서 \(\nabla_{\theta'} \bar{A}(\theta') = \nabla_{\theta'} J(\theta')\) 이므로 (VPG의 그것과 같으므로), 그냥 gradient ascent를 사용하면 되는걸까요?
아닙니다, 아직 constraint 가 추가되지 않았습니다.
 Slide. 20.
Slide. 20.
Gradient ascent (descent)를 그냥 한다는 것은 앞서 여러번 말씀드린 것 처럼 각 parameter의 policy에 대한 민감도를 전혀 고려하지 않은 것이 됩니다. 즉 어떤 parameter는 크게 한 step가도 문제가 없지만 어떤 paramter는 민감하기 때매 매우 조금만 가야 합니다.
Sergey는 앞서 제가 얘기했던 것 처럼 gradient descent가 사실은 아래와 같은 constraint가 걸린 optimization을 하는 것이라고 주장합니다.
\[\begin{aligned} & \theta^{\prime} \leftarrow \arg \max _{\theta^{\prime}} \nabla_{\theta} J(\theta)^{T}\left(\theta^{\prime}-\theta\right) & \\ & \text { such that }\left\|\theta-\theta^{r}\right\|^{2} \leq \epsilon & \\ \end{aligned}\]바로 현재 parameter point에서 parameter space내에 반경이 \(\epsilon\)인 원을 그리고, 그 안에서 objective 값을 최대화 하는 paramter를 고르겠다 (그 방향으로 한 step 가겠다) 라는 겁니다. 예를 들어 아래와 같은 2차원의 parameter 공간 (parameter space)이 존재한다고 할 때, x, y축이 각각 policy parameter를 나타내고 우리가 objective를 선형화했다고 하면 figure처럼 red, blue로 색칠된 gradient field로 나타낼 수 있습니다.
 Fig.
Fig.
오른쪽 아래 blue region은 더 나은 값 (better value)를 갖는 부분이고 왼쪽 위 red region 더 나쁜 값 (worse value)를 갖는 부분인데, 여기서 gradient ascent 가지는 constraint는 원 모양이 되는 것이고 (반경이 \(\epsilon\)인 원이 constraint 이므로), 이 부분에서 가장 나은 parameter을 찾는 것이 바로 1 step gradient descent이 됩니다. 이는 아래와 같이 수식으로 나타낼 수 있습니다.
\[\theta^{\prime} =\theta+\sqrt{\frac{\epsilon}{\left\|\nabla_{\theta} J(\theta)\right\|^{2}}} \nabla_{\theta} J(\theta)\]앞서 말씀드린 것 처럼 이것 또한 objective에 대해서 1차 근사를 하고 constraint에 대해서 2차 근사를 하면 얻을 수 있는데, 마치 step size를 gradient의 square root의 역수로 rescale해준 것이 RMSProp optimizer 같다는 걸 알 수 있습니다. 혹은 이 trust region을 잘 설정해주면 우리는 vanilla gradient descent도 얻을 수 있습니다.
 Fig.
Fig.
이를 parameter space상에서 반경 \(\epsilon\)짜리 원을 그린다고 해서 Euclidean Constraint라고 합니다.
이렇듯 trust region을 어떻게 설정해주느냐? 에 따라서 전혀 다른 gradient descent를 할 수도 있는 것입니다.
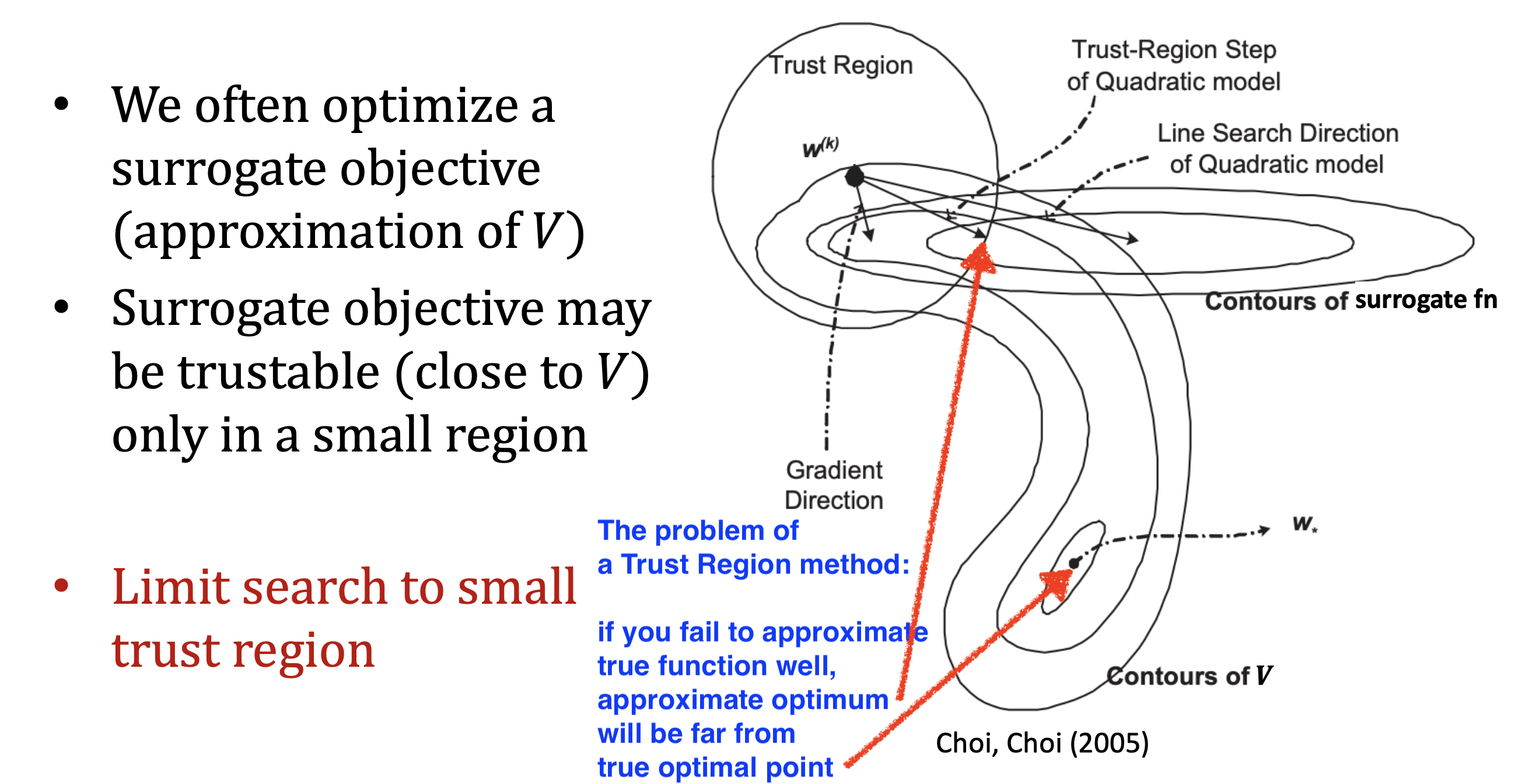 Fig. Source from CS885 by Pascal Poupart
Fig. Source from CS885 by Pascal Poupart
그런데 우리의 constraint는 parameter space상에서 정의된 것이 아니라 policy space 상에서 정의된 것 이었습니다. 거듭 말씀드리지만 우리는 approximate objective를 사용하고 있고, KLD constraint이 보장되어야만 policy improvement가 되는 방향으로 안전하게 update를 할 수 있습니다.
 Slide. 21.
Slide. 21.
앞서 objective에 대해서는 1차 근사를 했었고 constraint에 대해서는 2차 근사를 해야 한다고 했습니다. (왜 그런지에 대해서는 곧 추가 설명을 하도록 하겠습니다)
즉 \(D_{KL}\)를 \(\theta'=\theta\)인 지점에서의 2nd order taylor approximation을 해야 하는데, 이 2nd order approximation의 결과는 다음과 같습니다.
\[D_{K L}\left(\pi_{\theta^{\prime}} \| \pi_{\theta}\right) \approx \frac{1}{2}\left(\theta^{\prime}-\theta\right)^{T} \color{red}{ \mathbf{F} } \left(\theta^{\prime}-\theta\right)\]굳이 2차 근사를 하는 이유는 \(\theta'=\theta\)인 지점에서의 KL Divergence의 1st order term은 0이 되기 때문이며, 2차 근사 식에는 특이한 matrix, \(\mathbf{F}\)가 있는 것을 볼 수 있는데, 이를 Fisher Imformation Matrix라고 합니다. Fisher-Information Matrix에 대한 편리한 점 중 하나는 이 matrix가 expectation으로 표현되기 때문에 sampling으로 대체할 수 있고, 이는 우리가 PG를 하기 위해 sampling 했던 transition들을 사용할 수 있다는 겁니다.
\[\mathbf{F} = E_{\pi_{\theta}}[ \nabla_{\theta} \log \pi_{\theta}(\mathbf{a} \mid \mathbf{s}) \nabla_{\theta} \log \pi_{\theta}(\mathbf{a} \mid \mathbf{s})^{T} ]\]Fisher Information Matrix은 negative log likelihood의 expected hessian 이라고 하며, 의미적으로 parameter space상에서 log likelihood function이 휘어진 정도 (곡률; curvature)를 의미한다고 합니다. 왜냐하면 hessian은 어떤 function의 2차 미분항이기 때문에 그런 것이고, 값이 클수록 휨이 심각한 부분이기 때문에 loss function이 민감하게 반응한다는 의미로 해석이 될 수 있는 것이죠.
 Slide. 22.
Slide. 22.
그렇기 때문에 최종 수식에서 결국 fisher information matrix의 역행렬 (Inverse Matrix)인 \(F^{-1}\)을 gradient에 곱해 gradient를 보정해 주는 것이라고도 해석할 수 있겠습니다.
즉 gradient가 policy improvement를 보장하기 위한 gradient로 한층 자연스러워 졌기에 이를 Natural Gradient라고 부르며,
step size, \(\alpha\) 또한 fisher information matrix와 gradient를 통해 아래와 같이 계산할 수 있습니다. (아마 \(D_{KL} = \frac{1}{2} (\alpha \nabla_{\theta} J(\theta) - \theta)^T F (\alpha \nabla_{\theta} J(\theta) - \theta) = \epsilon\)으로 놓고 풀면 된다는 것 같다.)
\[\color{red}{ \alpha } = \sqrt{ \frac{ 2 \epsilon }{ \nabla_{\theta} J(\theta)^T \mathbf{F} \nabla_{\theta} J(\theta) } }\]마치 momentum과 adaptive step size를 적절히 적용해 준 모양새가 됐습니다.
마지막으로 gradient ascent (descent)와 다시 연관지어 insight를 얻어봅시다.,
Gradient ascent는 2차 제약식 (quadratic constraint or euclidean constraint), \(\parallel \theta-\theta' \parallel^2\)을 사용했었죠.
이는 \((\theta - \theta)^T (\theta - \theta) \color{red}{ \mathbf{I} }\)라고 나타낼 수 있는데,
사실 우리가 지금 사용한 것은 \((\theta - \theta)^T (\theta - \theta) \color{blue}{ \mathbf{F} }\) 였습니다.
그니까 natural gradient는 vanilla gradient ascent와 parameter space상에서 굉장히 비슷하면서도 다른 휘어진 constarint를 가진다가지게 됩니다.
어떤 점에서 모든 방향에 같은 constraint를 주는 \(\mathbf{I}\)와는 다르게 \(\mathbf{F}\)를 사용함으로써 constraint는 아래와 같이 변하게 되는 것입니다.
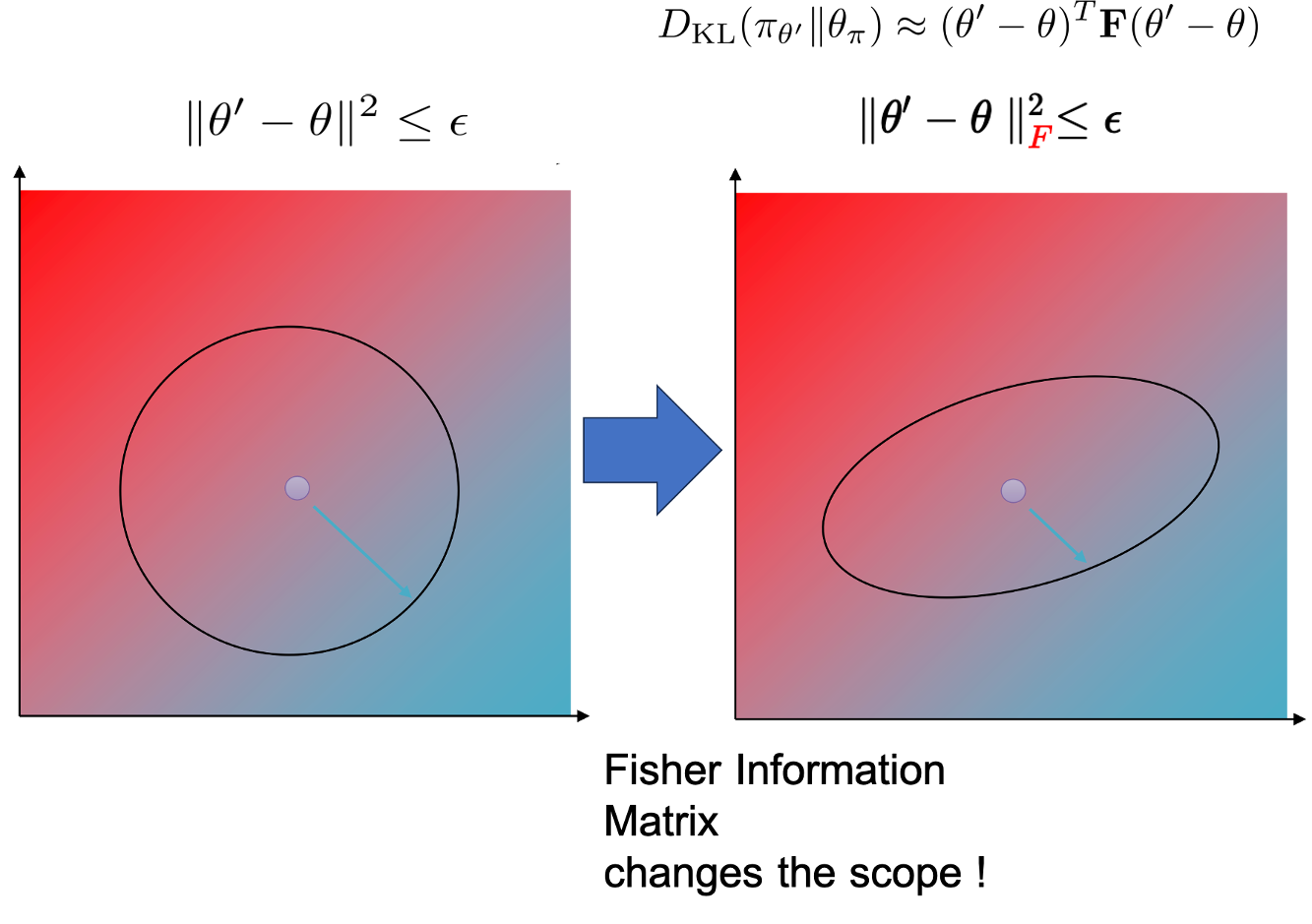 Fig.
Fig.
마지막으로 이를 algorithm 으로 표현하면 다음과 같은데, 우리는 2차 미분항인 Fisher Information Matrix만 구하면 policy가 망가지지 않는 선에서 최대한 크게 한 step감으로써 매 step 마다 policy improvement를 할 수 있다는 것이 보장되게 되는 것입니다.

(Locally) Off-policyness
Lecture에는 없지만 off-policyness는 매우 중요하니 언급을 잠깐 하도록 하겠습니다. 우리가 optimize하려는 objective function 은 다음과 같았습니다.
\[\bar{A}(\theta') = \sum_{t} E_{\mathbf{s}_{t} \sim p_{\theta}\left(\mathbf{s}_{t}\right)}\left[E_{\mathbf{a}_{t} \sim \pi_{\theta}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)}\left[\frac{\pi_{\theta^{\prime}}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)}{\pi_{\theta}\left(\mathbf{a}_{t} \mid \mathbf{s}_{t}\right)} \gamma^{t} A^{\pi_{\theta}}\left(\mathbf{s}_{t}, \mathbf{a}_{t}\right)\right]\right]\]이는 \(\pi_{100}\)으로 sampling한 trajectory들로 \(\pi_{100}, \pi_{100}, \cdots, \pi_{106}\) 같은 parameter를 update하는데 쓸 수 있다는 것을 의미합니다. 마치 EM처럼 계속 더 나은 bound를 형성하면서 최대한 주어진 sample을 재사용 할 수 있는 것이죠.
 Fig. Illustration of Expectation Maximization
Fig. Illustration of Expectation Maximization
이러니까 sample efficiency가 증가할 수 있는 겁니다. 다만 constraint은 여전히 필요하다는 걸 잊지 말아야 합니다. 더 많이 policy가 변화될수록 더 많이 constraint가 걸릴 겁니다. 당연히 imporatance sampling으로 두 policy의 같은 action에 대한 확률값도 보정을 해 줘야 하고요.
이 objective는 Q-Learing based method들 처럼 완전히 off-policy가 아닙니다. DQN같은 것들은 \(\pi_{1}\)이 만든 sample을 \(\pi_{500}\) update하는 데 써도 상관없었지만 지금은 그정도는 아닙니다. 그렇기 때문에 이를 그나마 sample한 parameter 근처에서는 (locally) off-policy가 성립하는 것이라고 생각할 수 있겠습니다.
A few details about the derivation of natural gradients
 Fig. Natural Gradient는 optimization problem을 objective function에 대해서 1차 근사, constraint에 대해서 2차 근사를 하면 풀 수 있다.
Fig. Natural Gradient는 optimization problem을 objective function에 대해서 1차 근사, constraint에 대해서 2차 근사를 하면 풀 수 있다.
 Fig. KLD에 대해서 2차 근사를 하는 이유는, 0차, 1차 근사항이 모두 0이 되어버리기 때문이다.
Fig. KLD에 대해서 2차 근사를 하는 이유는, 0차, 1차 근사항이 모두 0이 되어버리기 때문이다.
 Fig. 0차 항이 0이 되는 이유는 KLD의 정의를 사용하면 바로 알 수 있으며, 1차 항은 위 figure의 전개를 따르면 0이 된다.
Fig. 0차 항이 0이 되는 이유는 KLD의 정의를 사용하면 바로 알 수 있으며, 1차 항은 위 figure의 전개를 따르면 0이 된다.
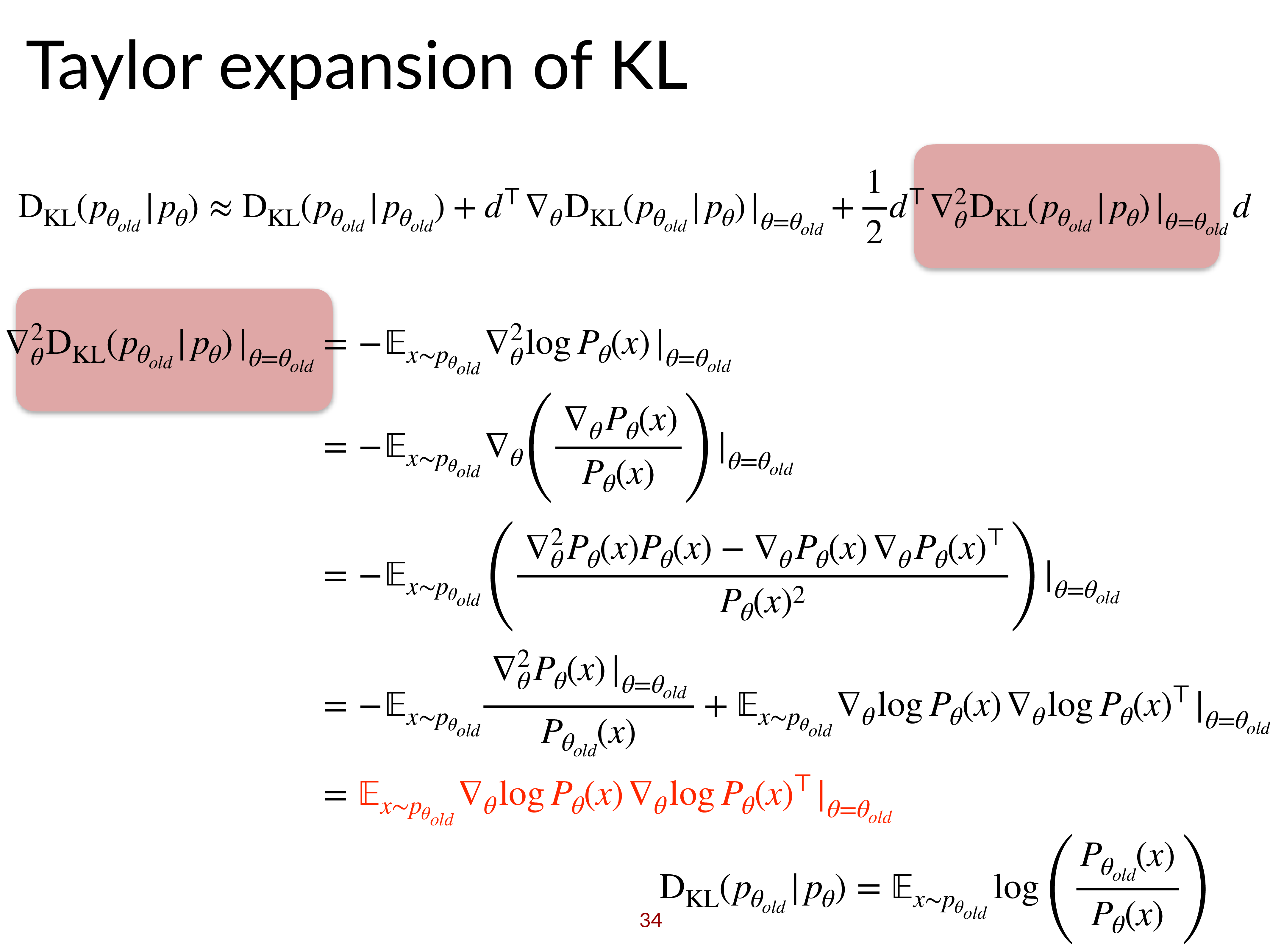 Fig. 2차 근사항은 Fisher Information Matrix가 유도된다.
Fig. 2차 근사항은 Fisher Information Matrix가 유도된다.
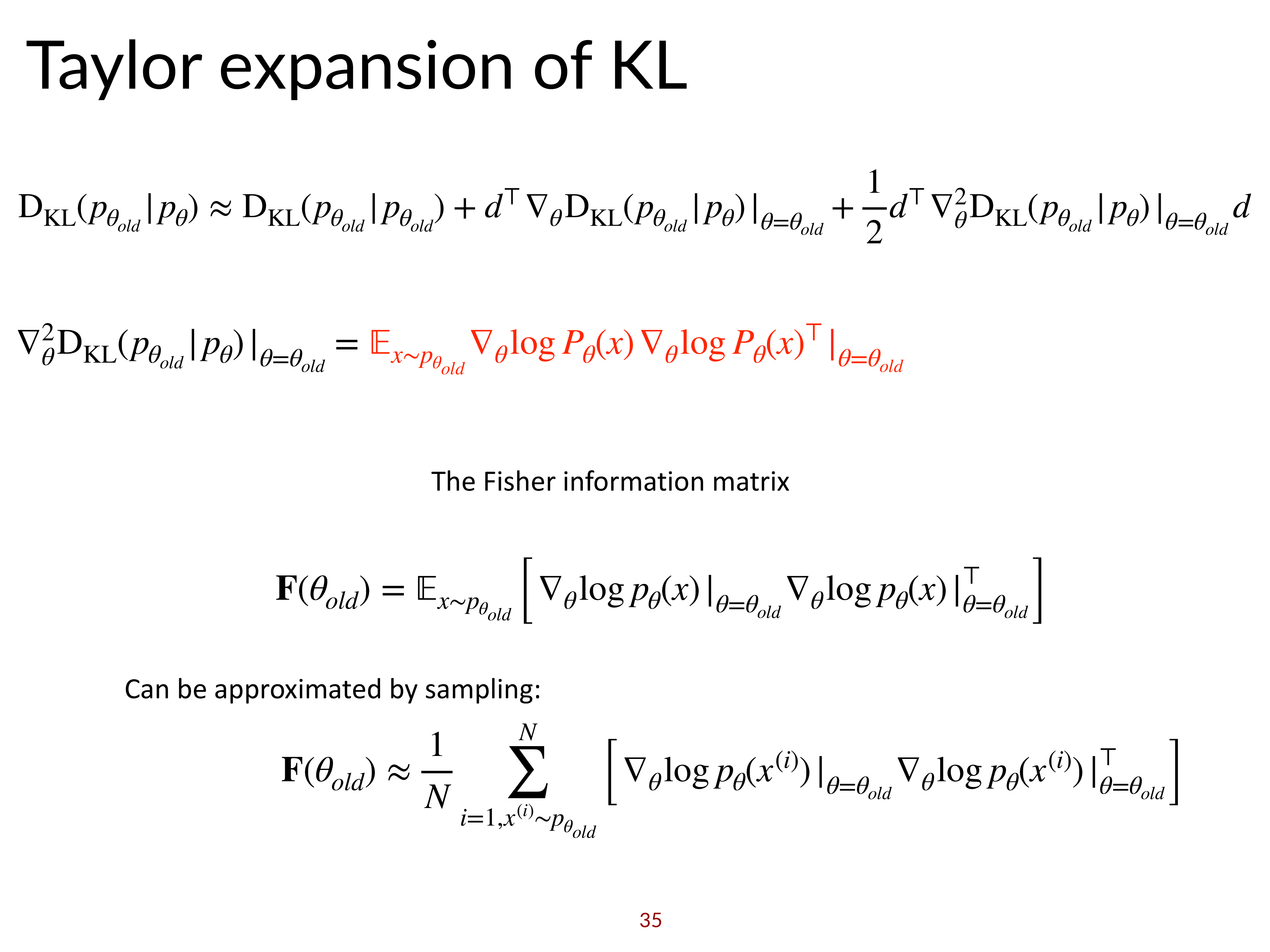 Fig. Fisher Information Matrix는 Sampling으로 근사 된다.
Fig. Fisher Information Matrix는 Sampling으로 근사 된다.
 Fig. 0이 되는 항은 모두 사라지고, \(\theta'\)에 대해서 미분을 할 때 상관없는 term들 또한 사라지게 된다.
Fig. 0이 되는 항은 모두 사라지고, \(\theta'\)에 대해서 미분을 할 때 상관없는 term들 또한 사라지게 된다.
 Fig. 미분을 해서 0인 지점을 찾으면 최종적으로 trust region에서 objetive를 maximize하는 paramter를 구할 수 있게 된다. 구해진 gradient는 PG에 Fisher Infromation Matrix의 inverse가 붙은 term이다.
Fig. 미분을 해서 0인 지점을 찾으면 최종적으로 trust region에서 objetive를 maximize하는 paramter를 구할 수 있게 된다. 구해진 gradient는 PG에 Fisher Infromation Matrix의 inverse가 붙은 term이다.
 Fig. 그리고 step size또한 Fisher Information Matrix로 구할 수 있게 된다.
Fig. 그리고 step size또한 Fisher Information Matrix로 구할 수 있게 된다.
Doesn't VPG have also proper constraint?
“아니 그냥 VPG (gradient ascent)도 constraint가 걸려있는거고 꽤 괜찮은 constraint인거 같은데 이렇게 까지 해야되나?”라는 생각이 들 수 있습니다. Sergey는 앞서 lecture 5에서 왜 VPG가 좋지 않은지를 위해 언급했던 example을 다시 보여줍니다. (똑같은 얘기 또 하니까 넘어가셔도 됩니다.)
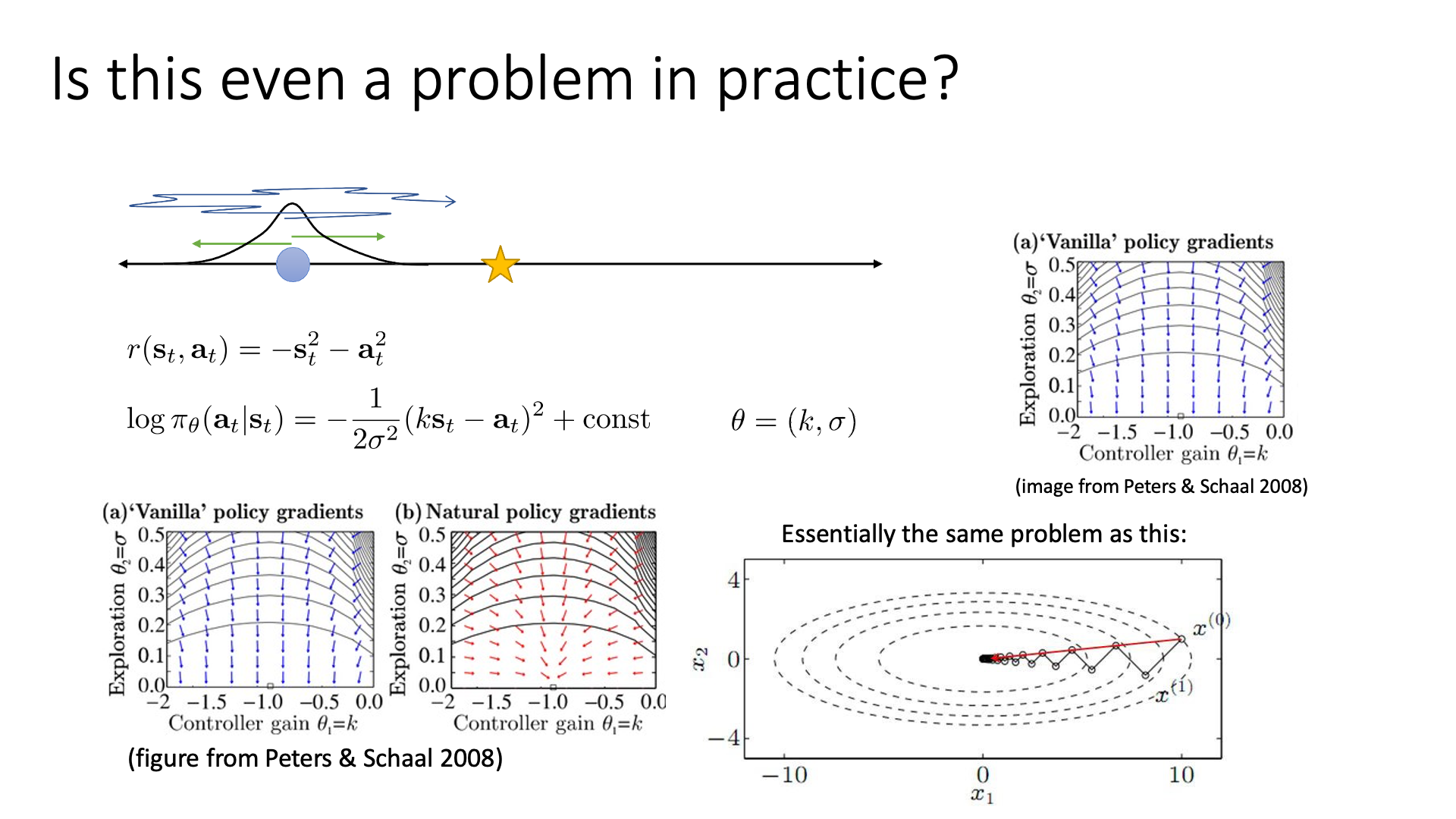 Slide. 23.
Slide. 23.
이 example의 goal은 star sign에 도달하는 겁니다. Tuning 해야할 paramter가 \(k,\sigma\) 두 개이며 star보다 왼쪽이면 오른쪽으로 가고 오른쪽이면 왼쪽으로 가는 일을 반복하면 됩니다. 여기서 VPG를 사용하는 경우 \(\sigma\)가 줄어들수록 \(\sigma\)에 관한 gradient가 \(k\)에 대한 gradient보다 훨씬 커지는 것을 볼 수 있습니다. 그러니까 \(k\)와 \(\sigma\)가 정책에 끼치는 영향력 다르기 때문에 (민감도가 다르기 때문에), \(k=-1\) 인 지점에 optimal solution이 존재하지만 이에 도달하기 굉장히 힘들어지는거죠. 이제 우리는 fisher information matrix를 곱한 NPG (우)가 VPG(좌)보다 왜 좋은지 어렴풋이 이해할 수 있게 되었습니다.
 Fig. vector field가 예쁘게 변한 것을 알 수 있다.
Fig. vector field가 예쁘게 변한 것을 알 수 있다.
Lecture Outro
마지막 slide에는 NPG 에 대한 몇 가지 note가 적혀있습니다.
 Slide. 24.
Slide. 24.
특히 3번째 부분이 중요한데, NPG는 optimization을 한 step수행하려면 그때마다 Full Fisher Matrix를 계산해야 하는 불편함이 있습니다. 이를 간단히 해서 fisher-vector (not matrix)를 사용해서 computational cost를 감소시킨 non-trivial solution도 있다고 하는데, 이것이 바로 그 유명한 Trust Region Policy Optimization (TRPO) 입니다. (line search나 off-policyness 등 몇 가지 trick들이 더 있는 것으로 아는데, 다른 post에서 깊게 다뤄보도록 하겠습니다.)
또한 우리가 앞서 구했던 importance sampled objective를 direct로 사용하는 algorithm이 있었는데, 바로 이것이 현재 policy-based algorithm들 중 가장 유명하고 성능이 잘 나와서 policy-based로 RL task를 풀려고 할 때 가장 먼저 시도해볼 만큼 강력한 algorithm이라고 알려져 있는 Proximal Policy Optimization (PPO) 입니다. (마찬가지로 TRPO와 다른 post에서 함께 깊게 다뤄볼 예정입니다.)
 Slide. 25. review 생략
Slide. 25. review 생략
Reference
- Papers
-
Lectures, Videos, Notes and Talks
- CS285
- Deep RL Bootcamp
- UCL x Deepmind Deep RL Lecture
- CMU 10-703 Deep Reinforcement Learning from Katerina Fragkiadaki
- Mutual Information
- Others
- OpenAI Spinning Up
- TRPO (Trust Region Policy Optimization) : In depth Research Paper Review
- Policy Gradient Algorithms from Lilian Weng
- Policy Optimization with Monotonic Improvement Guarantee from Runzhe Yang
- TRPO 논문 리뷰 from 노승은님
- Trust Region Policy Optimization (TRPO) 정리 from HiddenBeginner님
- Trust Region Policy Optimization, Schulman et al, 2015 from Chris Ohk
- Natural Policy Gradient 논문 리뷰 from Jangwon Kim
- Trust Region Policy Optimization 논문 리뷰 from Jangwon Kim
- Fisher Information from Hohyun Kim