(CS285) Lecture 6 - Actor-Critic Algorithms
09 Nov 2023이 글은 UC Berkeley 의 교수, Sergey Levine 의 심층 강화 학습 (Deep Reinforcement Learning) 강의인 CS285를 듣고 작성한 글 입니다.
Lecture 6의 강의 영상과 자료는 아래에서 확인하실 수 있습니다.
- Fall 2020 ver.
< 목차 >
- Recap
- Improving Policy Gradient (Lower Variance)
- From Policy Evaluation to Actor Critic
- Actor-Critic Design Decisions
- Improved Actor-Critic
- Review, Examples, and Additional Readings
- Outro
- Additional) Things to Think about
- Reference
 Slide. 1.
Slide. 1.
Lecture 5 에서는 Vanilla Policy Gradient (VPG) algorithm에 대해서 알아봤습니다.
그리고 VPG는 gradient estimate을 할 때 high variance 문제가 있었습니다
Lecture 6에서는 variance를 더 낮추기 위해 Actor-Critic이라는 algorithm에 대해 알아봅니다.
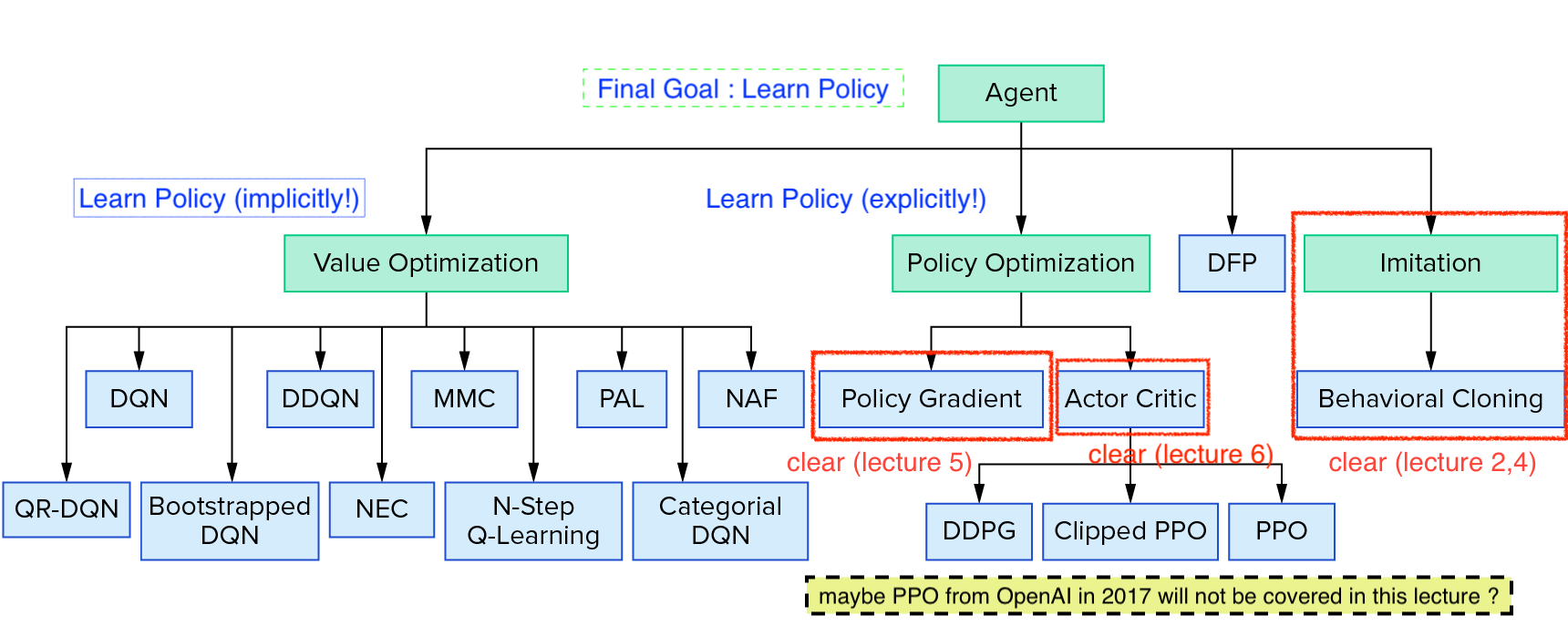
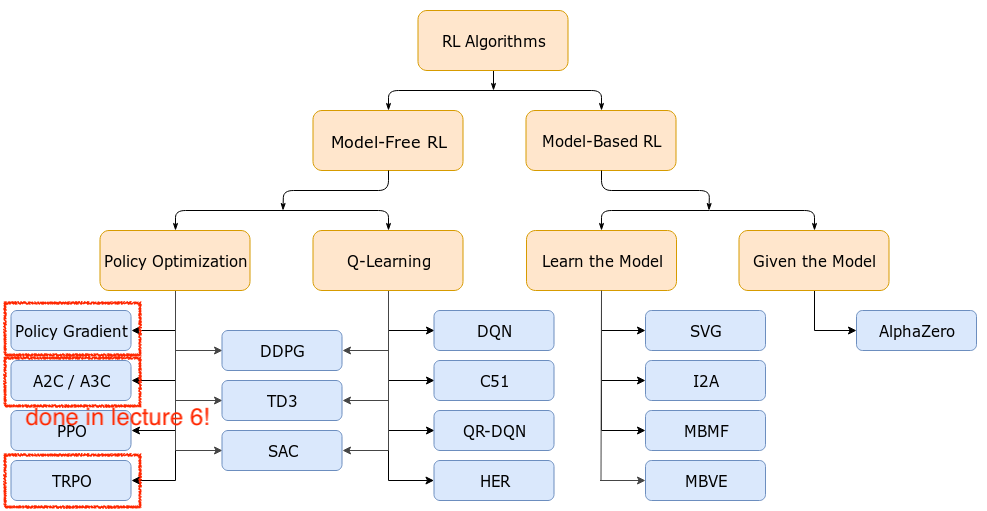
시작하기에 앞서 아래의 Deep Reinforcement Learning (RL)의 Taxonomy를 봅시다.
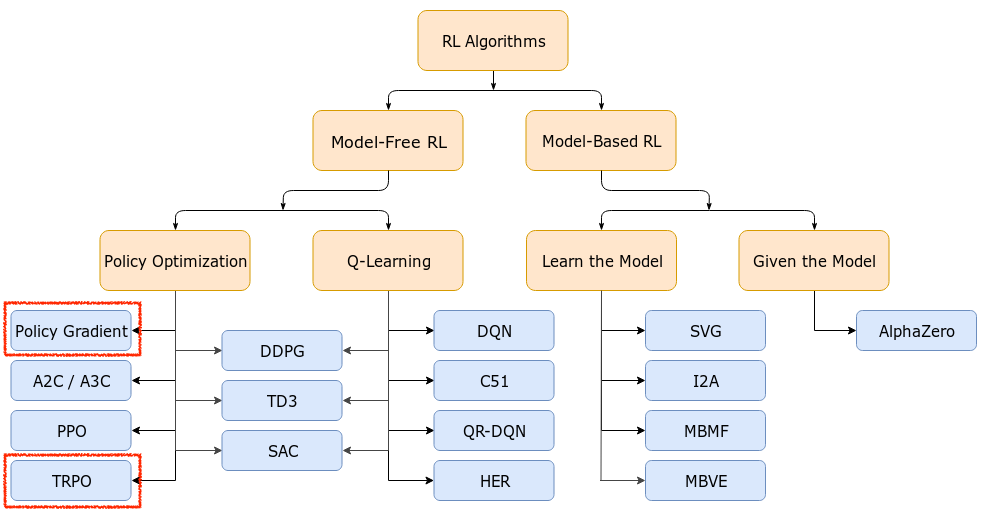 Source from OpenAI Spinning Up form OpenAI
Source from OpenAI Spinning Up form OpenAI
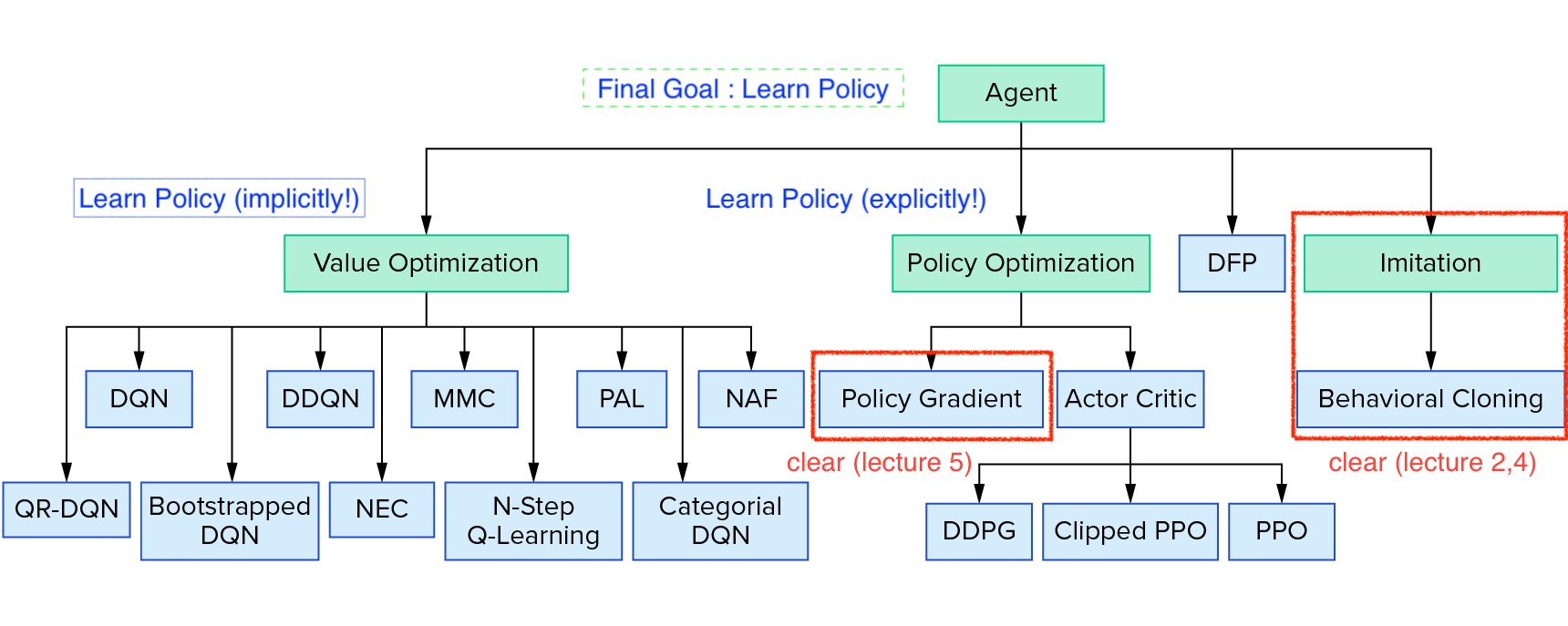 Source from Reinforcement Learning Coach from Intel Lab
Source from Reinforcement Learning Coach from Intel Lab
Taxonomy에 보시면 Policy Gradient (Optimization)계열의 algorithm을 보시면 Actor-Critic의 가장 기초가 되는 Advantage Actor-Critic (A2C),
이를 하나의 processor가 아닌 여러 processor로부터 만든 sample 들을 만들어 학습하는 Asynchronous Advantage Actor-Critic (A3C),
그리고 Trust Region Policy Optimization (TRPO)와 Proximal Policy Optimization (PPO) 라는 algorithm들이 있습니다.
Lecture 6에서는 A2C와 A3C까지 다루고 Lecture 9에서 TRPO, PPO에 대해서 살짝 배웁니다.
Actor-Critic은 figure들에서 볼 수 있듯 Policy Optimization 으로 분류되기는 하지만, policy-based method와 value-based method를 결합한 것이라고 할 수 있습니다.
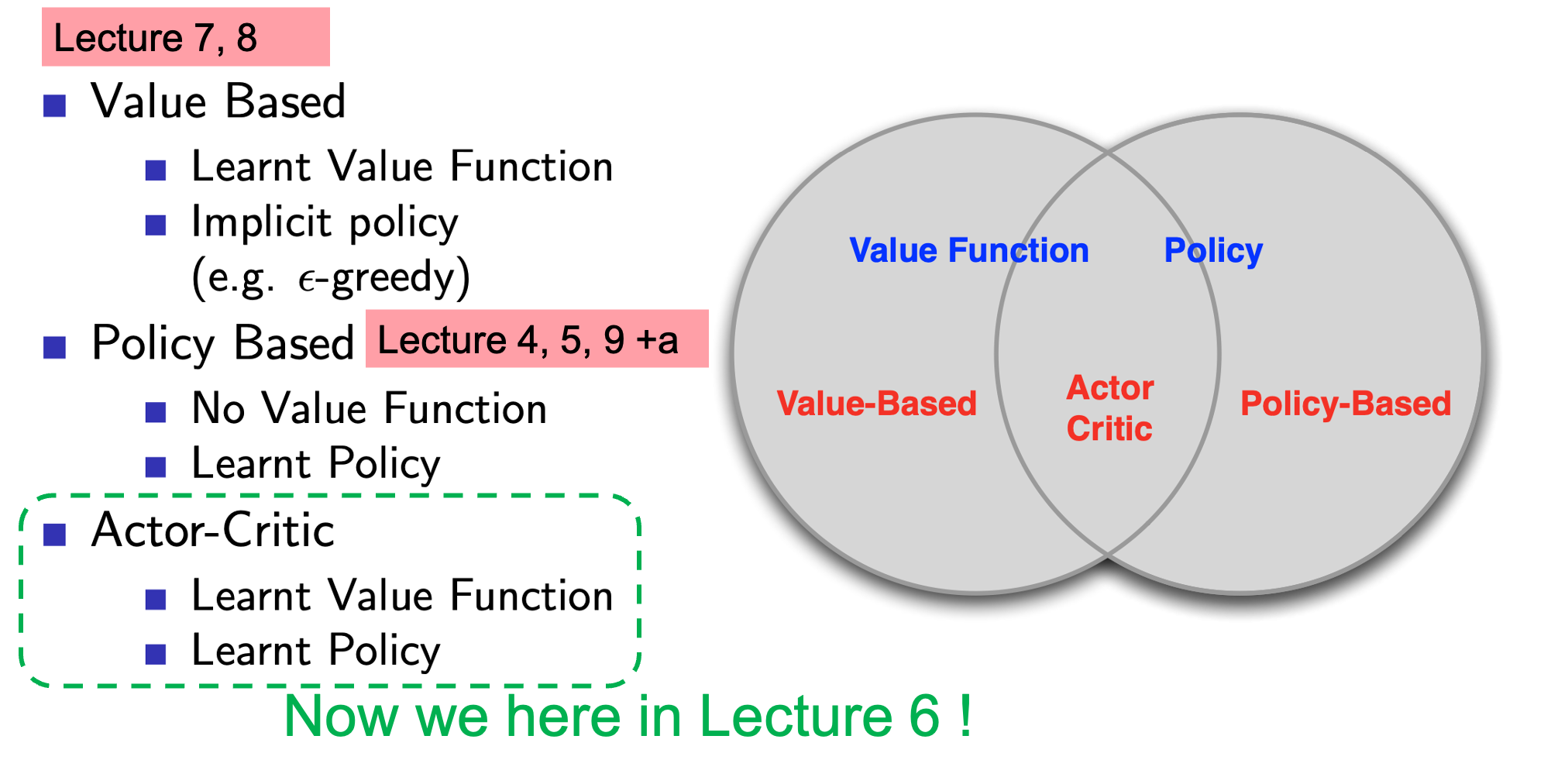 Fig. Actor-Critic은 Policy-based method와 Value-based method를 결합한 algorithm이다.
Fig. Actor-Critic은 Policy-based method와 Value-based method를 결합한 algorithm이다.
이제 Actor-Critic 이 무슨 algorithm인지 본격적으로 알아보도록 합시다.
Recap
PG는 trajectory를 여러번 sampling한 뒤 이 trajectory들이 어땠는지를 evaluate하고 loss를 policy에 대해 미분해 gradient를 구해서 direct policy optimization을 수행합니다.
지난 lecture에서 trajectory의 cumulative sum을 \(Q^{\pi} (x_t,u_t)\) 라고 정의했는데, 이를 reward-to-go라고 부르기로 했습니다.
직관적으로 VPG를 통해 policy는 미래에 reward를 더 많이 발생시킬 action은 더 likely하게 만들고, 그 반대는 unlikely하게 확률을 낮춥니다.
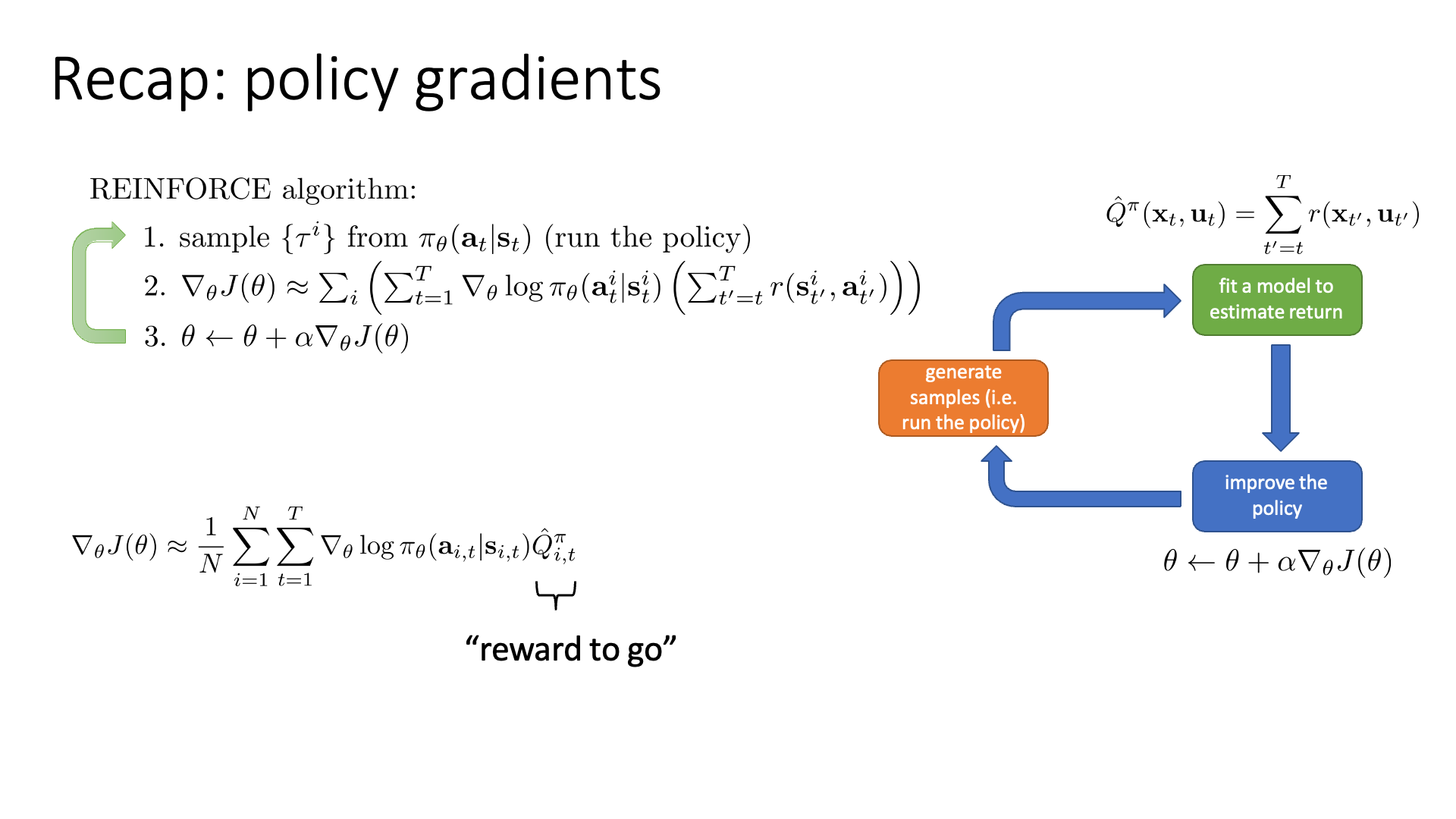 Slide. 2.
Slide. 2.
Improving Policy Gradient (Lower Variance)
그러나 VPG는 몇 가지 문제가 있습니다.
- PG의 3가지 Main Problem
- High Variance 하다.
- 최적화 시 Step Size, \(\alpha\) 를 고르기 어렵다.
- Sample Inefficiency 하다.
PG 계열 algorithm들은 대부분 위의 3가지 중 하나를 해결하기 위해 제안되었다고 할 수 있겠습니다. Actor-Critic도 target 하는건 똑같은데, 이번 lecture에서는 마찬가지로 high variance에 대해서 얘기합니다.
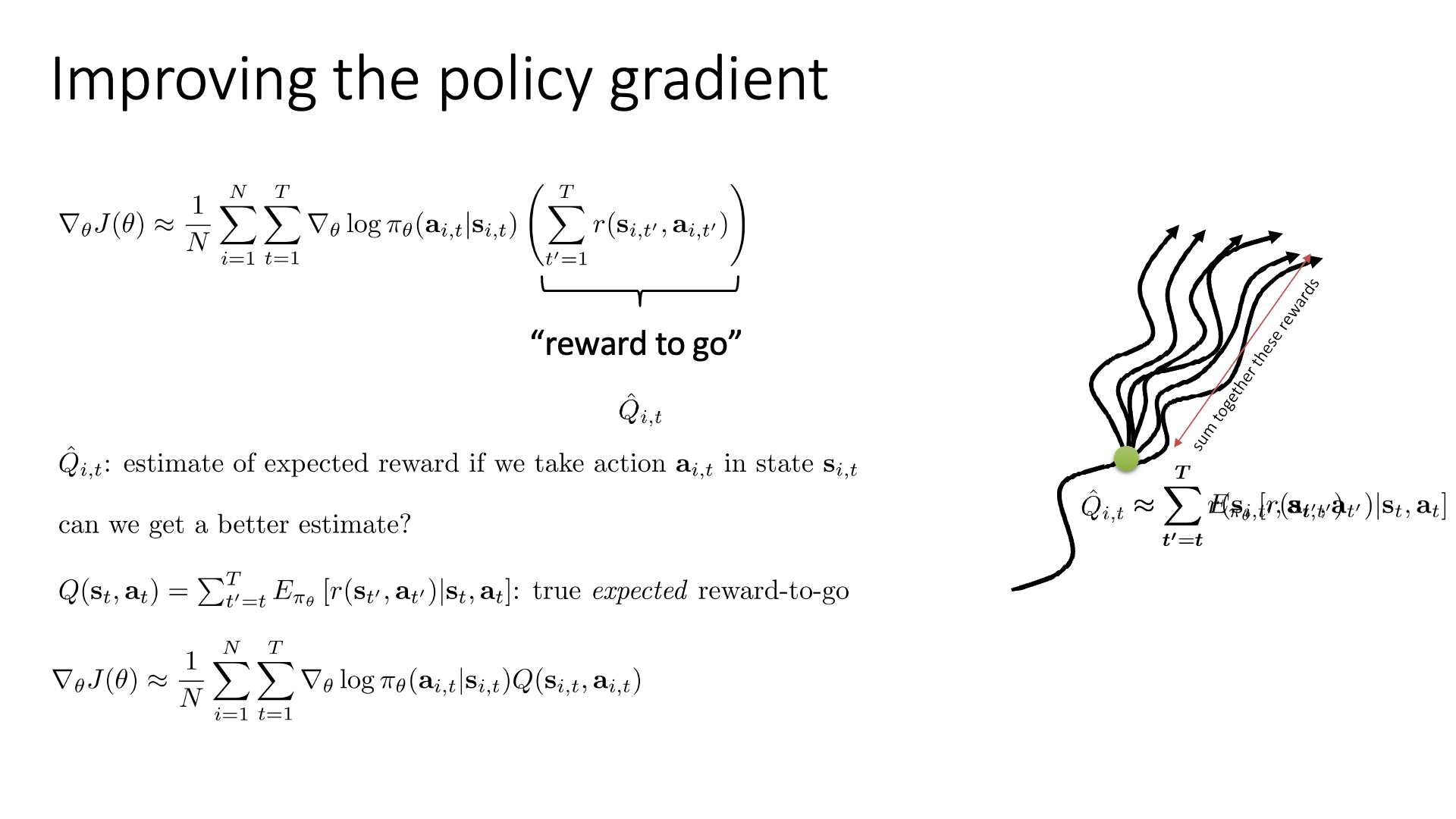 Slide. 3.
Slide. 3.
Reward-to-go, \(Q^{\pi} (x_t,u_t)\)에 대해서 조금 더 얘기해봅시다.
이 Q라는 quantity는 수식을 해석했을 때 어떤 state에서 어떤 action을 했을 때 (action을 이미 했음), policy를 따라서 terminal state 까지 가 봤을때 얻을 수 return을 의미합니다.
즉 이 action이 얼마나좋았는지?를 의미하는데, 이를 단순히 끝까지 한 번 가본 뒤 얻은 reward들의 합을 그 값으로 쓰는 건 너무 단순해 보입니다.
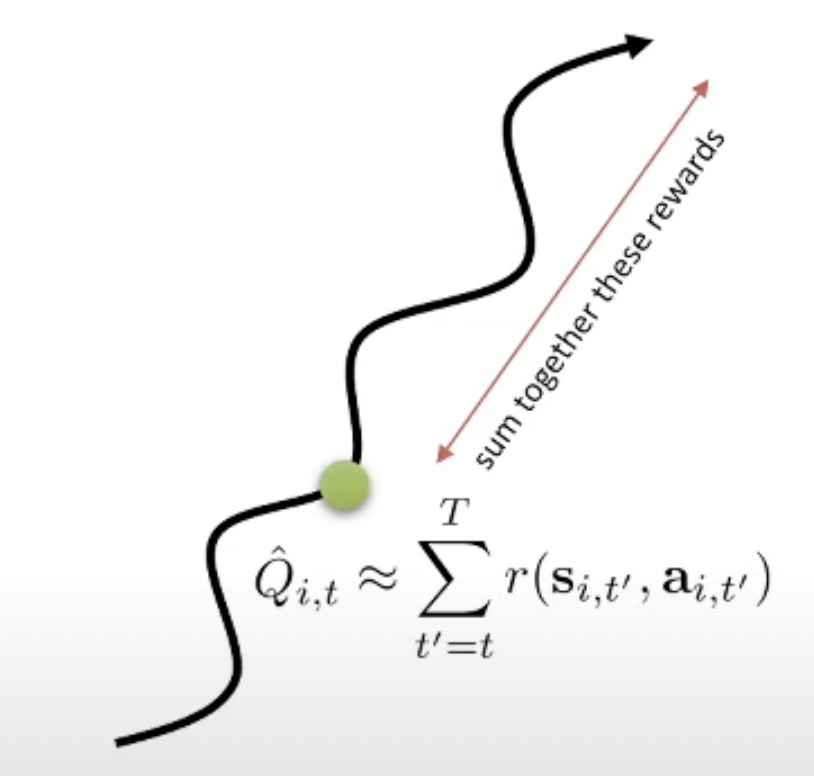
이 행동의 reward을 더 잘 measure 하려면 어떻게 해야 할까요? 한 가지 대안은 어떤 시점 \(t'\) 에서의 액션을 평가할 때, 현재 가지고있는 정책을 가지고 한 번이 아니라 여러 번 끝까지 가보고 (sampling) 이 reward값들의 평균 (정확히는 expectation)을 쓰는겁니다.
\[\begin{aligned} & \hat{Q_{i,t}} \approx \sum_{t'=t}^T \color{red}{\mathbb{E}_{\pi_{\theta}}} [ r(s_{t'},a_{t'}) \vert s_t,a_t ] & \\ \end{aligned}\]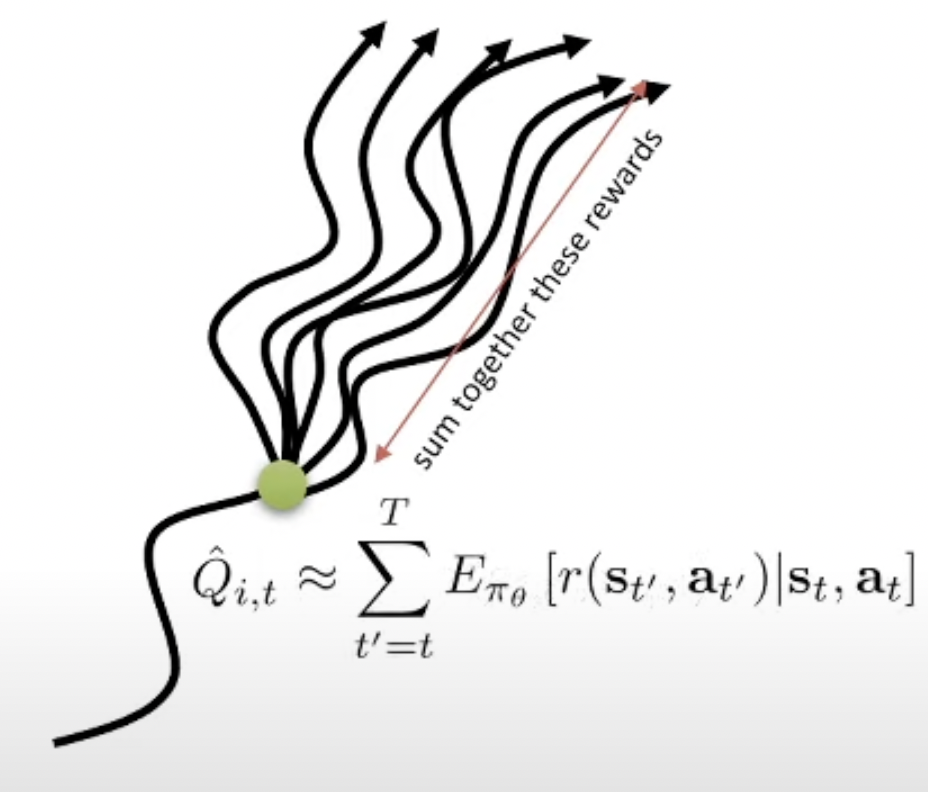
왜냐하면 앞서 말했 듯 VPG는 굉장히 variance가 큰 이유가 우리가 우연히 같은 state에 도착한다고 해도 그 t시점의 \(s_t\)에서 같은 action, \(a_t\)를 한다해도, 끝까지 한 번 가 볼 경우 environment나 policy의 randomness 등 때문에 다른 return을 받을 수 있기 때문입니다. 즉 variance가 이렇게 큰 상황에서 1회 sampling한걸 쓰는건 도박같은 거죠.
그러므로 sampling을 여러번 해서 평균을 내면 mean 값에 가까운 결과를 얻을 수 있을테니, 이를 쓰자는 겁니다. 당연히 무한번 sampling하면 (Full Expectatio을 계산하는 것과 같음) 아무런 문제가 없겠으나 이는 당연하게도 계산 불가합니다. 그러므로 적당히 10번정도 sampling 하는것으로 만족해야 합니다 (trade-off).
그런데 우리가 Full Expectation을 계산할 수 있다고 칩시다.
이를 True expected reward-to-go, 혹은 True Q-Function 이라고 합니다.
이 Q값은 우리가 lecture 4에서 정의한 state-action value function이 맞습니다. 아예 수식적으로 같은 의미를 가지고 있고, 이는 \(\hat{Q}\)과 다르게 approximation (\(\approx\))이 아닙니다. 이제 우리는 true Q-function을 사용한 PG의 objective는 아래처럼 다시 쓸 수 있게 됩니다.
\[\begin{aligned} & \nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i-1}^N \sum_{t=1}^T \nabla_{\theta} \log \pi_{\theta} (a_{i,t} \vert s_{i,t}) \hat{Q_{i,t}} & \\ & \nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i-1}^N \sum_{t=1}^T \nabla_{\theta} \log \pi_{\theta} (a_{i,t} \vert s_{i,t}) \color{red}{Q(s_{i,t},a_{i,t})} & \\ \end{aligned}\]Applying Baseline
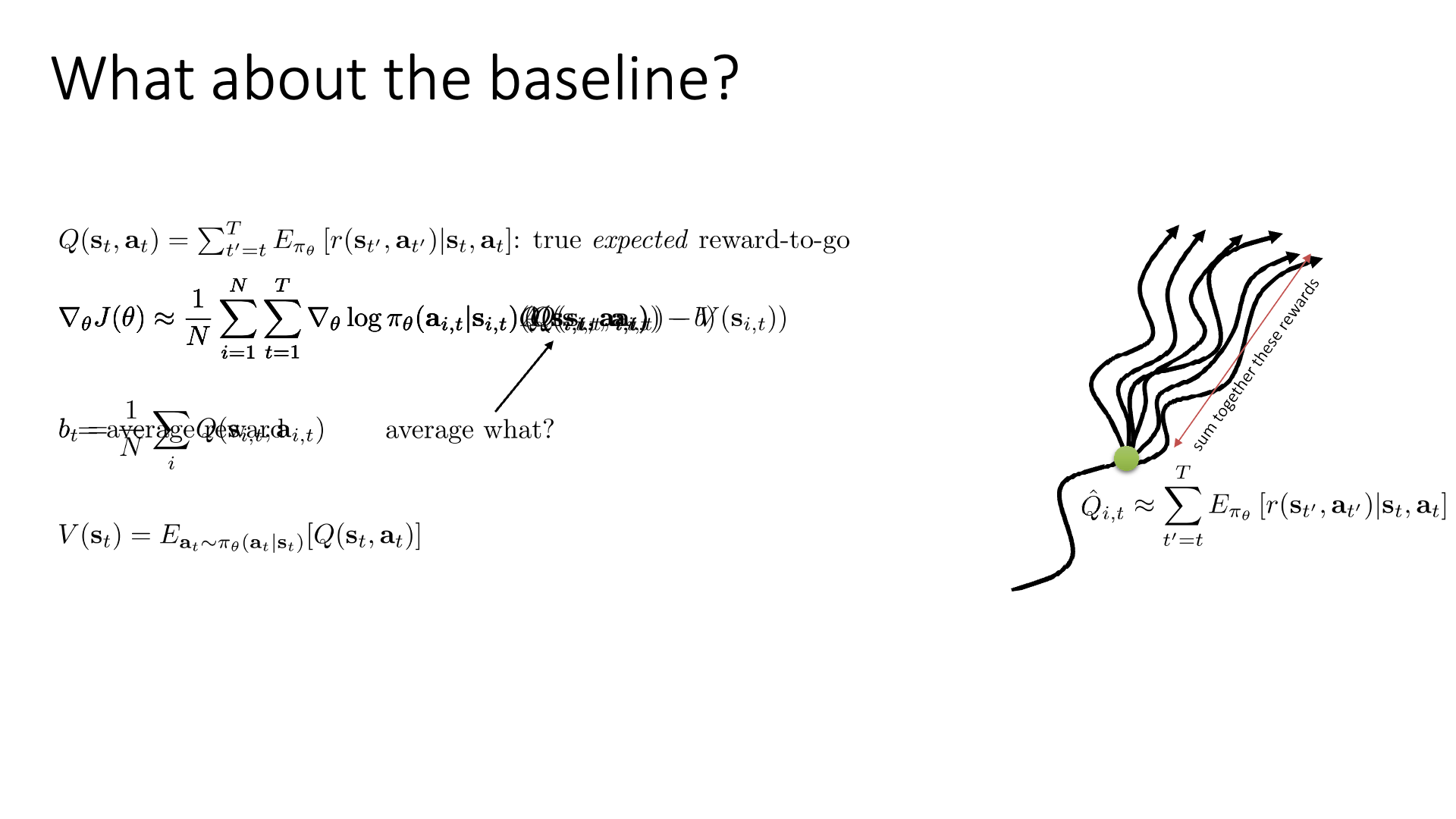
이제 이 수식에 지난 VPG처럼 baseline을 적용하려고 합니다.
그런데 그냥 적용해도 될까요?
Sergey는 당연히 가능하다고 합니다. 그 이유는 (지난번에 배운 형태의 trajectory들의 Return을 평균 내는) baseline을 빼는건 여전히 unbias 이기 때문입니다 (expectation값을 바꾸지 않음).
 Slide. 4.
Slide. 4.
5장에서 baseline, \(b\)를 우리가 sampling한 trajectory들에 대한 reward의 평균,
즉 average return로 설정하는게 꽤 괜찮다고 했었으니 비슷한 baseline으로 써보려고 합니다.
(baseline이 단순히 trajectory의 return을 평균낸 것이 아니라 뭔가 time dependent한 것으로 바뀌었는데, 그렇게 이상한 term은 아닙니다. 아마 Sergey가 다른 quantity를 쓰고 설명을 생략한게 아닌가 싶습니다.)
여기서 variance를 좀 더 줄여봅시다. 우리가 baseline을 고를 때 주의할 점은 expectation을 unbias하게 만들면서 variance를 줄이기만 하면 된다는 겁니다. Sergey는 여기서 V라는 quantity를 사용해보자고 합니다. (Lecture 4의 state value function)
\[V(s_t) = \mathbb{E}_{a_t \sim \pi_{\theta} (a_t \vert s_t)} [Q(s_t,a_t)]\]기존의 Q를 사용한다는 것은 \(s_t\)에서 policy 분포에 따라 어떤 \(a_t\)를 sampling 해 보고, 이를 끝까지 가본 것들의 평균을 쓰는 것이었습니다.
하지만 V, Value Function (가치 함수) 는 수식에서도 (정의에사도) 알 수 있듯 \(s_t\)에서 가능한 action \(a_t\) 를 다 해보고 그 action들을 각 각 했을 때 끝까지 가본 것들의 평균을 평균낸 것으로 Q에 expectation을 취한겁니다.
Sergey는 gradient estimator를 unbias하게 유지하게 위해서는 \(s,a\)에 모두 의존하는 quantity보다는 state, \(s\)에만 의존하는 것을 쓰는게 낫다고 합니다. (그리고 아마 time dependent baseline보다 현재 state 기준 sampling이 1회라도 덜 들어갔기 때문에 low variance라는건 직접 variance를 계산하지 않아도 직관적으로 이해가 될 것 같습니다)
 Fig. constant baseline 외에 다양한 baseline을 쓸 수 있다.
Fig. constant baseline 외에 다양한 baseline을 쓸 수 있다.
Baseline을 V Function으로 선택했기 때문에 수식적으로 log of action probability에 곱해지는 값이 \(Q(s_t,a_t)-V(s_t)\)가 되었습니다.
그런데 이 의미는 매우 직관적이고 말이 됩니다.
‘어떤 state에서 어떤 action을 선택 하는 것의 expected return이 그 state에서 모든 action에 대한 expected return의 평균보다 얼마나 좋은가?’를 log prob에 곱해주게 된거죠.
우리가 constant baseline을 썼을때는 고작 ‘이 trajectory가 다른 trajectory보다 얼마나 좋은가?’를 measure했는데,
이제는 time step별로 비교를 하게 된거죠.
이 \(Q-V\)라는 quantity는 RL에서 굉장히 중요한 qunatity인데,
이를 Advantage Function, \(A\) 라고 부릅니다.
Intuition for Advantage Function
 Fig.
Fig.
어떤 state, \(s_1\)에서 할 수 있는 모든 action들의 평균 평가 점수가 +3000이었습니다.
그리고 \(s_2\)의 모든 action들의 평균 점수는 -4000 이었습니다.
이럴 경우 \(s_2\)에서도 분명 좋은 action이 있을 수 있고, \(s_1\)에서도 나쁜 action이 있을 수 있겠죠?
 Fig.
Fig.
그런데 문제는 \(s_2\)의 good action이 -3970인 평균보다 30점이 높은 점수이고 \(s_1\)의 bad action이 평균보다 300점 낮은 2700점 짜리 action이어도 gradient에 영향을 더 많이 줄 action은 \(s_1\)의 bad action이 될거라는 겁니다.
그래서 우리는 각 state에서 평균 점수를 꼭 빼는 등의 처리를 해줘야 하는 겁니다.
 Fig.
Fig.
Three Important Quantities: Q, V and A
조금 정리해봅시다.
 Slide. 5.
Slide. 5.
State-action value function, Q function은 \(s_t\)에서 행동 \(a_t\)를 취했을 때, 이후 현재 가지고 있는 정책을 통해 episode가 끝날때까지 돌려보고 매 step마다의 reward값들을 전부 더한 것의 expectation 입니다 (expected return).
\[Q(s_t,a_t) = \sum_{t'=t}^T \mathbb{E}_{\pi_{\theta}} [r(s_{t'},a_{t'}) \vert s_t,a_t]\]Q Function에는 보통 아래와 같이 윗첨자에 \(\pi\)를 추가하여 표시하곤 하는데,
\[Q^{\pi}(s_t,a_t) = \sum_{t'=t}^T \mathbb{E}_{\pi_{\theta}} [r(s_{t'},a_{t'}) \vert s_t,a_t] \quad \scriptstyle{\text{ total reward from taking } a_t \text{ in } s_t}\]이는 Q Function가 policy \(\pi\)에 의존한다는걸 강조하기 위한 겁니다. Policy optimization이 일어나 policy가 uddate 될 때 마다 \(\pi\)가 달라지므로 당연히 Q값도 달라집니다.
\[V^{\pi}(s_t) = \mathbb{E}_{a_t \sim \pi_{\theta}(a_t \vert s_t)} [Q^{\pi}(s_t,a_t)] \quad \scriptstyle{\text{ total reward from } s_t}\]V Function은 Q의 expectation으로, \(s_t\)에서 \(a_t\)를 했을 때의 expected return이 아니라 \(s_t\)에서 모든 action을 고려했을 때의 expected return 입니다. 즉 Q의 weighted sum version인 것이죠. 마지막으로 우리는 앞서 말한 것 처럼 Q와 V의 차이를 아래처럼 advantage function로 정의해 표시할 수 있습니다.
\[A^{\pi} (s_t,a_t) = Q^{\pi}(s_t,a_t) - V^{\pi}(s_t) \quad \scriptstyle{\text{ how much better } a_t is}\]이 세 가지 quantity는 RL을 이해하는데 있어 매우 매우 중요하므로 한번 더 기억해주시길 바랍니다.
\[\begin{aligned} & \color{red}{Q^{\pi}(s_t,a_t)} = \sum_{t'=t}^T \mathbb{E}_{\pi_{\theta}} [r(s_{t'},a_{t'}) \vert s_t,a_t] & \scriptstyle{\text{ total reward from taking } a_t \text{ in } s_t} \\ & \color{blue}{V^{\pi} (s_t)} = \mathbb{E}_{a_t \sim \pi_{\theta}(a_t \vert s_t)} [ \color{red}{Q^{\pi}(s_t,a_t)} ] & \scriptstyle{\text{ total reward from } s_t} \\ & A^{\pi} (s_t,a_t) = \color{red}{Q^{\pi}(s_t,a_t)} - \color{blue}{V^{\pi} (s_t)} & \scriptstyle{\text{ how much better } a_t \text{ is}} \\ \end{aligned}\]
Q를 reward-to-go로, V를 baseline 으로 쓴 gradient를 아래와 같이 계산할 수 있는데, A값이 정확할수록 vaiance가 더 낮아지므로 더 안정적인 학습을 할 수 있습니다.
\[\nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \sum_{t=1}^T \nabla_{\theta} \log \pi_{\theta} (a_{i,t} \vert s_{i,t}) \color{green}{A^{\pi} (s_{i,t}, a_{i,t})}\]하지만 여기서 문제는 실제 algorithm이 동작할 때 당연하게도 정확한 A값을 알 수는 없다는 겁니다.
지금까지 A는 true Q function을 가정했는데 full expectation을 계산하는 일은 실제로는 불가능 하기 때문이죠.
그래서 우리는 이 function를 approximate하려고 합니다.
물론 이 approximation이 원본에 가까울수록 variance는 더 낮아질겁니다.
당연히 Deep RL이니까 우리는 NN을 사용해서 Q나 V function을 approximate할겁니다.
즉 policy \(\pi\)를 위한 Neural Network (NN)가 이미 있고,
여기에 추가로 또 다른 NN이 \(A\)를 approximate하는 형태이므로 NN이 2개거나 그 이상이 필요하게 됩니다 (Q, V둘다 modeling하면 3개).
여기서 \(\pi\)는 어떤 state에서 어떤 action을 해야하는지를 return하는 Actor이고, A를 approximate한 NN은 (가능한 모든 action들 대비) 이 action이 얼마나 좋았는가?를 평가하는 것이므로 행동을 평가하는 Critic라고 이름 짓습니다.
그렇기에 이런 형태의 algorithm을 Actor-Critic이라고 하는 겁니다.
(마치 Generative Adversarial Networks (GANs) 처럼)
여기서 한 가 지 더 언급해야만 하는 것은 여태까지의 VPG는 variance를 줄이면서도 여전히 unbiased했지만,
이제는 Q값을 approximate하기 때문에 NN이 잘못 expected return을 예측하면 policy에도 bias가 생기는 상황이 발생한다고 합니다.
만약 NN이 비슷한 input (state)에 대해서 overfitting을 그리 심하게 하지 않고, 일반화 (Generalization)가 잘 되면,
비슷한 trajectory의 비슷한 action 에 대해 Critic이 추론하는 값이 꽤 일정할 것이므로 low variance해 졌다고 볼 수 있겠죠.
그러나 비슷한 trajectory들에 대해 10점, 10.5점, 10.23점… 이라고 주는 건 좋으나,
NN이 10점짜리 action을 만약 13점으로 잘못 예측하면 (13점, 13.5점, 13.23점 …) 그 만큼의 bias는 거죠.
당연히 우리가 approximator를 학습하기로 했으니 이는 감수해야 하는겁니다.
즉 학습만 잘하면 (little) biased, lower variance 인 gradient estimator를 얻게 되는 겁니다.
Fit What to What ? (fit V !)
다시 lecture로 돌아갑시다. 아래의 anatomy를 다시 보시면 green box가 좀 더 detail 하게 바뀌었음을 알 수 있습니다. 원래는 return을 estimate 한다는 것은 그 상태에서 한 번 끝까지 가보고 environment가 리턴해준 값을 합치는 것으로 끝이었으나 더는 그렇지 않습니다.
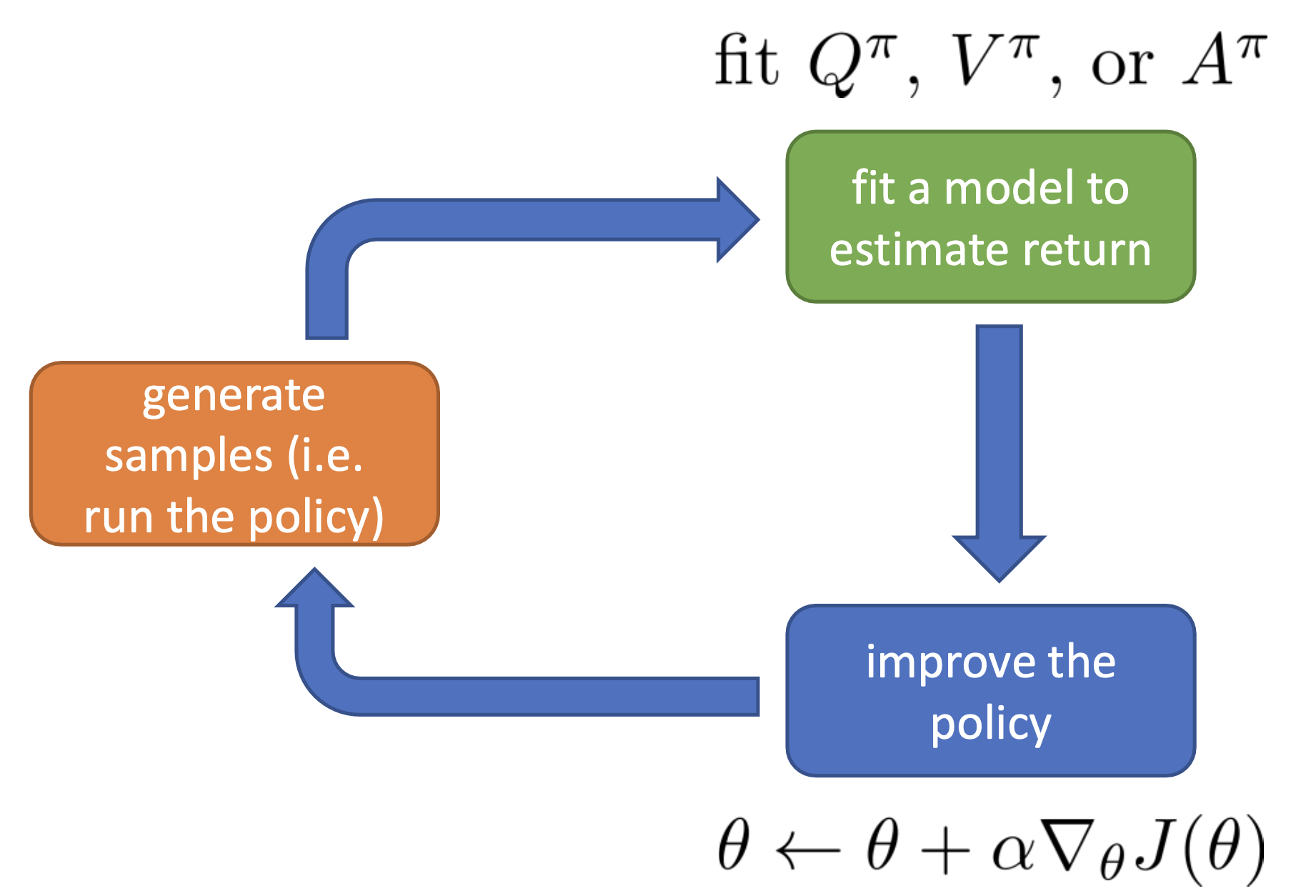 Fig. Anatomy of Deep RL
Fig. Anatomy of Deep RL
이 녹색부분인 Fitting Value Function 부분을 좀 더 살펴보도록 하겠습니다.
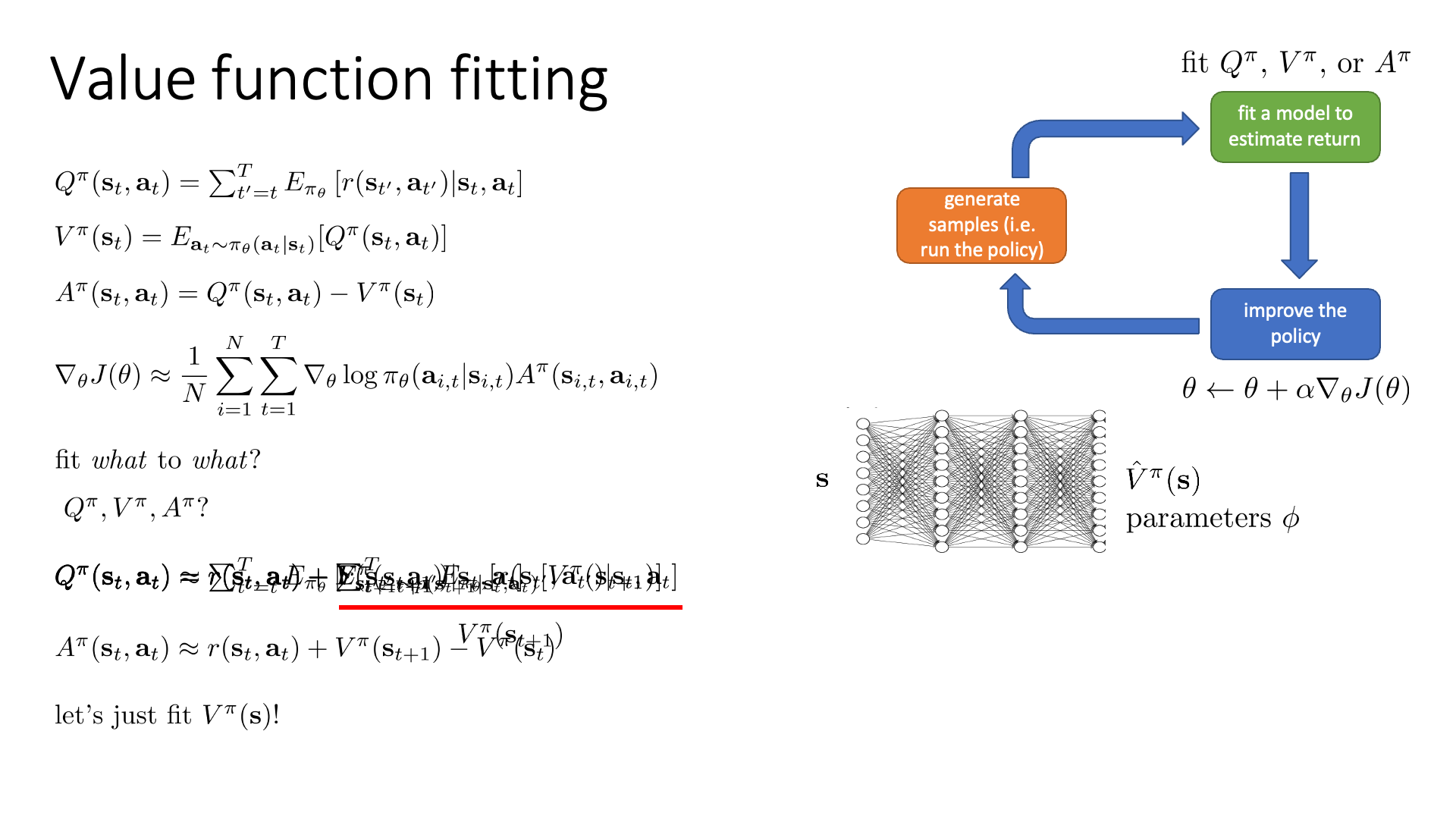 Slide. 6.
Slide. 6.
과연 Q, V, A중에서 어떤 값을 학습해야 할까요? 무엇을 target으로 학습해야 할까요? 이 부분에 대해서 얘기해 봅시다.
fit what to what?
먼저 Q에 대해서 다시 얘기해봅시다.
Q의 의미는 현재 state에서 어떤 action을 취했을 때 그 뒤로의 expected return입니다.
여기서 \(s_t\)에서 \(,a_t\)을 한다는 사실 자체가 이미 일어난 일이므로 더이상 t시점의 element들은 random variable이 아닙니다.
그러므로 수식을 아래와 같이 다시 쓸 수 있습니다.
여기서 우변의 두 번째 항은 아래와 바꿀 수 있습니다.
\[\begin{aligned} & Q^{\pi}(s_t,a_t) = r(s_t,a_t) + \underbrace{\sum_{t'=t+1}^T \mathbb{E}_{\pi_{\theta}} [r(s_{t'},a_{t'}) \vert s_t,a_t]}_{ \color{red}{V^{\pi}(s_{t+1})} } & \\ & Q^{\pi}(s_t,a_t) = r(s_t,a_t) + \mathbb{E}_{s_{t+1} \sim p(s_{t+1} \vert s_t,a_t)}[V^{\pi}(s_{t+1})] & \\ \end{aligned}\]즉 \(s_t\)에서 \(a_t\)를 한 것은 정해졌기 때문에 current reward를 environment로 부터 받고,
그 뒤로는 또 모든 action을 고려한 expected return이므로 정확하게 V값이 됩니다.
다만 우리가 \(s_t\)에서 \(a_t\)를 함으로써 어떤 \(s_{t+1}\)로 갔는지는 알아야 거기서 \(V\)를 취할 수 있습니다.
즉 transition probability를 알아야 한다는 조건이 포함된건데 이는 VPG에 없던 가정입니다.
우리가 원하는 진짜 값인 \(\mathbb{E}_{s_{t+1} \sim p(s_{t+1} \vert s_t,a_t)} [V^{\pi}(s_{t+1})]\) 를 구해내기는 어려우니,
여기에 approximate (approximation)를 한 번 어쩔 수 없이 해야합니다.
(아니면 다른 방법이 있긴 한데, \(s_t,a_t\)를 여러 번 해서 \(V(s_{t+1})\)를 여러 번 구해서 평균을 취하는 겁니다만 cost가 너무 많이 들죠)
위의 수식이 의미하는 바는 next-time step의 state에 대한 분포를 이전에 해왔던 것 처럼 a single sample estimator로 approximate하는 겁니다.
하지만 주의해야 할 점은 딱 그 한스텝만 한번 sampling하는것이고 그 뒤로는 여전히 모든 값을 고려하는 Expectation을 계산한다는 겁니다.
그러므로 approximate으로 variance가 조금 증가하긴 했으나 나쁘지 않은 estimator가 됩니다.
(sampling을 할수록 variance 증가)
하지만 이렇게 \(Q\)를 근사함으로써 좋은 점이 있는데, 우리가 baseline으로 \(V\)를 쓰기 때문에 Advantage Function, \(A\)를 \(V\)로만 구성할 수 있게 됐습니다.
\[\begin{aligned} & \color{red}{Q^{\pi}(s_t,a_t)} \approx r(s_t,a_t) + V^{\pi}(s_{t+1}) & \\ & A^{\pi}(s_t,a_t) = \color{red}{Q^{\pi}(s_t,a_t)} - V^{\pi}(s_{t}) & \\ & A^{\pi}(s_t,a_t) \approx \color{red}{r(s_t,a_t) + V^{\pi}(s_{t+1})} - V^{\pi}(s_{t}) & \\ \end{aligned}\]이제 수식이 \(V^{\pi}\)에만 전적으로 의존하게 되었고, 이로인해 \(V\)를 modeling한 NN만 하나 더 있으면 됩니다. (원래는 Q, V 둘다 따로 학습해야 했을 수도 있음)
추가로 Q와 A는 \(s_t,a_t\) 에 대한 function이었으나 V는 \(s_t\)에 대한 function이기 때문에 NN의 input 변수가 줄어들어 approximate하기가 더 쉬워졌습니다.
이제 input으로 state를 바다 scalar value를 뱉어주는 NN을 학습하면 되는데, 이는 \(\phi\)로 parameterize 되어있습니다.
(policy는 \(\pi\)로 파라메터화 되어있음)
 Fig. s만 받아서 scalar값을 뱉어주는 NN을 학습하면 된다.
Fig. s만 받아서 scalar값을 뱉어주는 NN을 학습하면 된다.
물론 \(Q\)를 modeling해도 됩니다. 뒤에서 \(Q^{\pi}\)를 직접 approximate하는 방법론에 대해서도 살펴볼 것이라고 합니다.
Policy Evaluation and Monte Carlo Estimator
이제 Actor-Critic의 기본적인 뼈대를 거의 완성했습니다.
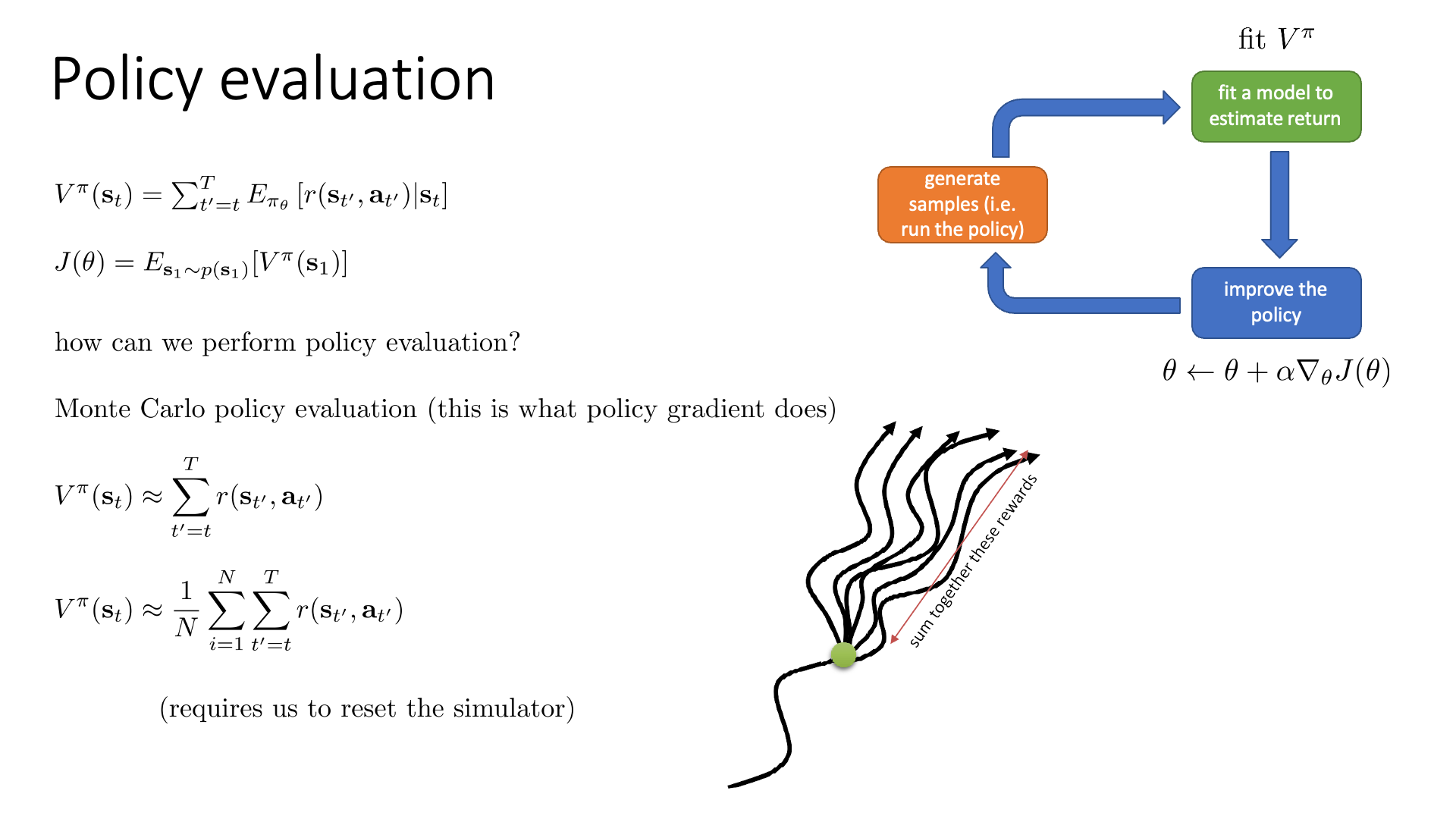 Slide. 7.
Slide. 7.
남은 것은 어떻게 \(V^{\pi}(s)\)를 계산할 것이냐? 인데, 왜냐하면 우리는 \(s_t\)가 주어졌을 때,
거기서부터 파생 가능한 trajectory들의 return들의 총 합 (엄밀히는 expectation)을 예측하는 NN을 만들어야 함으로 어떤 값을 target으로 할까?에 대한 문제를 풀어야 하기 때문입니다.
한 편, \(V^{\pi}(s)\)를 피팅하는 과정은 일반적으로 Policy Evaluation이라고도 합니다.
그 이유는 \(V^{\pi}(s)\)가 매 state마다 policy의 가치를 평균 낸 값을 return하기 때문입니다.
왜 이것이 policy evaluaion인지에 대한 제 생각은 다음과 같습니다. 수식에서 알 수 있듯 V는 그 \(s_t\)에서 가능한 \(a_t\)들을 했을때의 각각 일어날 수 있는 return값들을 모두 계산하고, 그 action들의 확률을 보정해준 값입니다 (왜냐면 기대 값이므로 \(a_t \sim \pi({a_t \vert s_t})\)). 그런데 만약 policy가 잘못 학습되었다면? 실제로는 좋은 return을 만들어내는 action에 낮은 확률이 할당되면서 V값이 작아질 겁니다. 반대로 잘 학습됐다면 policy가 좋은 action에는 높은 확률을 할당함으로써 V가 굉장히 높아지겠죠? 이런 의미에서 V를 재는것은 policy를 평가하는 의미를 가지게 되는 겁니다.
또한 우리가 원하는 RL의 Objective는 모든 state에서 받은 reward를 전부 합친 것 (Return)을 최대화 하는 것인데, 이는 초기 상태인 \(s_1\)의 가치 함수의 expectation과 동치가 된다고 합니다. (갑자기 이 얘기는 왜 한건지 모르겠지만)
\[J(\theta) = \mathbb{E}_{s_1 \sim p(s_1)} [ V^{\pi} (s_1) ]\]어쨌든 어떻게 V 값을 계산할까요? 어떻게 하면 policy evaluation을 할 수 있을까요?
\[V^{\pi} (s_t) = \sum_{t'=t}^T \mathbb{E}_{\pi_{\theta}} [r(s_{t'}, a_{t'}) \vert s_t]\]당연히 expectation을 다 계산할 수 없으니 이런 고민을 하게 되는 것인데, 그 중 하나는 앞서 우리가 했던 것과 같이 sampling을 하는겁니다.
expectation을 sampling 몇 번으로 대체하여 그 추정치를 결과값으로 쓰는 것을 통계학, machine learning에서는 Monte Carlo method라고 부릅니다.
이는 VPG이 작용하는 방식과도 같은 것이죠.
자 sampling을 1회 할 수도, 수 회를 할 수도 있습니다. Lecturer는 당연히 아래처럼 수 회 sampling 하는것이 좋겠으나 이것이 가능하려면 simulator를 끝까지 한 번 가보고, 다시 되돌렸다가 (reset) 또 가보고 … 등등을 반복할 수 있는 상황이어야만 이렇게 여러 번 하는 것이 가능하기에 여러번 policy evaluation을 할 수 있고 당연히 그런 값을 쓰는게 더 좋다고 합니다.
\[V^{\pi} (s_t) \approx \frac{1}{N} \sum_{i=1}^N \sum_{t'=t}^T r(s_{t'},a_{t'})\]하지만 그렇지 않은 상황에서는 딱 한 번 가보는 것의 결과값을 사용해야 한다고 말합니다.
\[V^{\pi} (s_t) \approx \sum_{t'=t}^T r(s_{t'},a_{t'})\]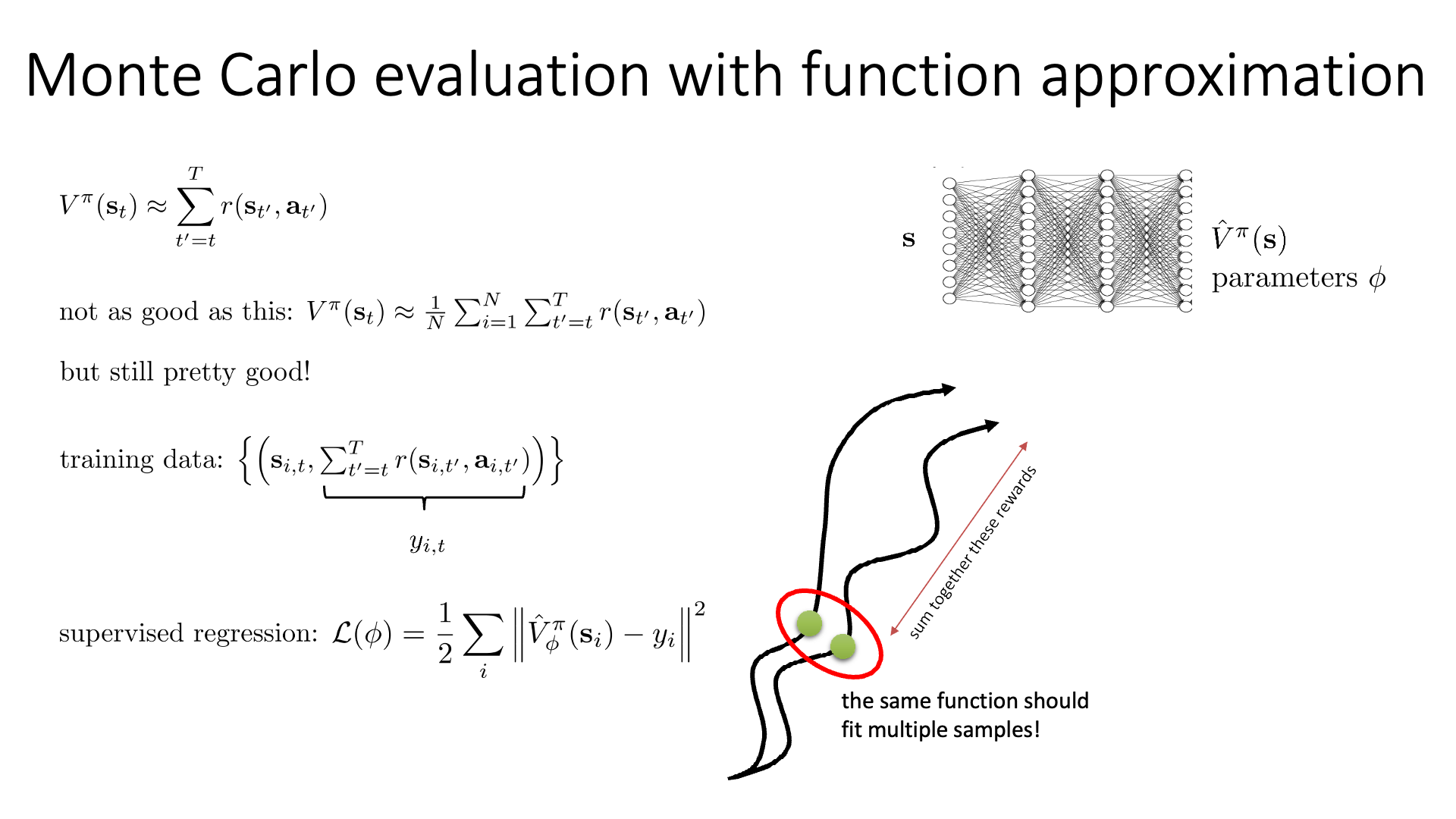 Slide. 8.
Slide. 8.
여기서 우리가 Monte Carlo 방법으로 수십번 가본 것을 target으로 NN을 학습하는것에 굉장히 중요한 insight가 있습니다.
왜 directly policy gradient 하던 것에 value network를 NN으로 approximate한 값을 쓴걸까요?
다시, V값을 baseline으로 쓰는건 좋습니다만 NN으로 굳이 예측을 하지 않고 매번 값을 구하고 PG와 연결하면 되는데 왜 NN을 두개 씩이냐 두냐는 말입니다.
그리고 하필이면 다른 algorithm도 아니고 NN으로 V를 approximate하는 이유는 뭘까요.
그 이유는 NN이 앞서 말씀드린 것 처럼 generalization을 잘 하는 function approximator입니다.
예를 들어 어떤 연속적인 state space를 갖는다고 칩시다. 당연하게도 아무리 sampling을 열심히 해봐야 똑같은 곳을 다시 방문할 수는 기회는 별로 없을것이지만, 비슷비슷한 상황에는 자주 노이게 될겁니다. (자율주행 simulator를 생각하면 정확히 똑같은 장면은 아니겠으나 비슷한 풍경과 도로 상황은 많이 보이겠죠)
뭐 우리가 4x4 격자구조의 미로찾기 문제를 푼다고 하면 state는 16개 이므로 똑같은 곳에 방문하는 일이 굉장히 많을 것이니 신경쓰지 않아도 되지만 실제로 그런일은 없을겁니다.
우리는 이 state들이 어떤 값을 받아야 하는지, 즉 현재 이 state 에서 이 policy에 따라 가능한 action들을 모두 해 본다고 치면 몇점을 받는지, 내가 얼마나 좋은 상태에 놓여있는지에 대한 걸 알아야 이 값을 바탕으로 action을 update할 수 있습니다. 그런데 당연히 모든 state에 방문할 수 없으니 제대로 학습하려면 무한에 가까운 sampling이 필요하게 됩니다 (거의 모든 state를 방문하기 위해서) 게다가 앞서 variance를 얘기하면서 정확히 같지는 않아도 우리는 비슷한 상태에서는 비슷한 값을 return하길 원하죠?
그런 의미에서 우리는 value function을 학습해야 하고, 하필이면 NN으로 이를 approximate하는 것입니다.
이제 우리가 계산한 V값을 target으로 회귀 (Regression) 하는 NN을 우리는 지도학습 (Supervised Learning)하면 됩니다.
출력이 scalar 값이죠? 다르게 말하면 연속적인 분포인 gaussian distribution을 target distribution으로 쓰는 것이 되므로 일반적인 Mean Squared Error (MSE) Loss를 써서 학습을 하면 되겠습니다.
이제 우리는 가치 함수 네트워크가 심하게 overfitting 하지 않으면, 즉 일반화에 성공한다면 더 낮은 variance, 적당한 bias의 gradient estimator 얻을 수 있습니다.
Bootstrapped estimator
하지만 아직도 부족합니다. 우리가 어떤 상태에서 직접 시뮬레이션을 끝까지 돌려서 얻은 V를 타겟으로 하지 말고 true expected value of rewards를 사용할 순 없을까요?
아니 아까 sampling 아니면 불가능에 가깝다고 했는데 어떻게 이걸 할 수 있을까요
 Slide. 9.
Slide. 9.
실제 ideal target은 expectation 그 자체였습니다.
\[\begin{aligned} & y_{i,t} = \sum_{t=t'}^T \mathbb{E}_{\pi_{\theta}}[r(s_{t'},a_{t'}) \vert s_{i,t}] & \scriptstyle{ \text{ideal target} } \\ & y_{i,t} = \sum_{t=t'}^T r(s_{i,t'},a_{i,t'}) & \scriptstyle{ \text{Monte Carlo (MC) Traget (one sample)}} \\ \end{aligned}\]위의 ideal target을 조금 바꿔봅시다.
우리가 이전에 Q Function을 아래와 같이 current reward + 다음 스텝에서의 \(V^{\pi}\)로 approximate할 수 있었습니다.
이러한 사실을 이용해서 idea target도 approximate를 할 수 있는데
이러한 타겟을 사용하는게 매 번 한번씩만 sampling하는 몬테카를로 방법보다는 더 낮은 variance의 솔루션을 얻을 수 있게 해줄 수 있다고 합니다. 여기서 우리는 \(V^{\pi}\)를 모르기 때문에 마찬가지로 이를 approximate한 NN의 output, \(\hat{V}_{\phi}^{\pi}(s_{i,t+1})\)을 사용해야 합니다.
\[\begin{aligned} & y_{i,t} \approx r(s_{i,t},a_{i,t}) + \color{red}{\hat{V}_{\phi}^{\pi}(s_{i,t+1})} & \\ \end{aligned}\]이런 값을 bootstrap estimator라고 부르는데, RL에서 bootstrap이란 보통 어떤 실제 값이 아닌 추정치,
즉 NN의 output을 또 다시 어떤 값을 update하는 데 쓰는 것 등을 bootstrapping한다고 합니다.
(bootstrap이 부츠 끈을 하나 당기면 나머지도 당겨진다는 느낌으로, 연쇄적으로 진행되는? 어떤 self-improvement를 의미한다는 말도 있습니다. Computer Vision 의 Representation Learning 분야의 Bootstrap your own latent: A new approach to self-supervised Learning이라는 논문을 보면, EMA teacher의 output vector를 student의 target으로 써서 학습을 하는데 이것도 어떻게보면 추정치를 다시 target으로 쓰는 방식으로 self-improvement하는 형태이므로 bootstrap이라고 할 수 있는 것이죠. 약간 뇌피셜입니다.)
(in BYOL paper)
...
Our approach has some similarities with Predictions of Bootstrapped Latents (PBL, [49]),
a self- supervised representation learning technique for reinforcement learning (RL).
이렇게 해서 우리는 target을 single sample estimator가 아니라 bootstrap estimator로 바꿀 수 있습니다.
\[\begin{aligned} & \text{training data : } (s_{i,t}, \sum_{t'=t}^T r(s_{i,t'},a_{i,t'}) ) & \\ & \text{training data : } (s_{i,t}, r(s_{i,t},a_{i,t}) + \hat{V}_{\phi}^{\pi} (s_{i,t+1}) ) & \\ \end{aligned}\]이러한 bootstrap estimator는 한번 sampling한것을 타겟으로 하는 것 보다 lower variance를 가지기 때문에 좋지만, 이 approximate 함수가 뱉는 값이 부정확할 것이기 때문에 bias는 클 수 있다고 합니다 (trade-off). (하지만 학습이되면서 이 값이 정확해지면 bias는 줄어들 것 같습니다.)
What The Heck Policy Evaluation Actually Means in Real-World Example ?
그런데 Policy Evaluation에 대한 직관적인 이해가 아직 부족할 수 있습니다.
 Slide. 10.
Slide. 10.
Slide에는 TD-Gammon 과 AlphaGO 예시가 있는데, 여기서 AlphaGO를 예로 들어 간단하게 설명드려보도록 하겠습니다. 그 유명한 AlphaGO의 원 논문 제목은 Mastering the game of Go with Deep Neural Networks & Tree Search입니다.
AlphaGO는 현재 바둑판의 상태를 보고 최적의 수를 두는 network를 학습하는 것이 목표입니다.
그렇다면 당연히 action을 두는 network인 policy network \(\pi\)가 필요할 것이고, 당연하게도 더 짧은 시간에 더 좋은 지점으로 수렴하기 위해서는 좋은 PG algorithm이 필요하므로, value network도 필요합니다.
즉 Actor-Critic manner로 학습하는 것이죠.
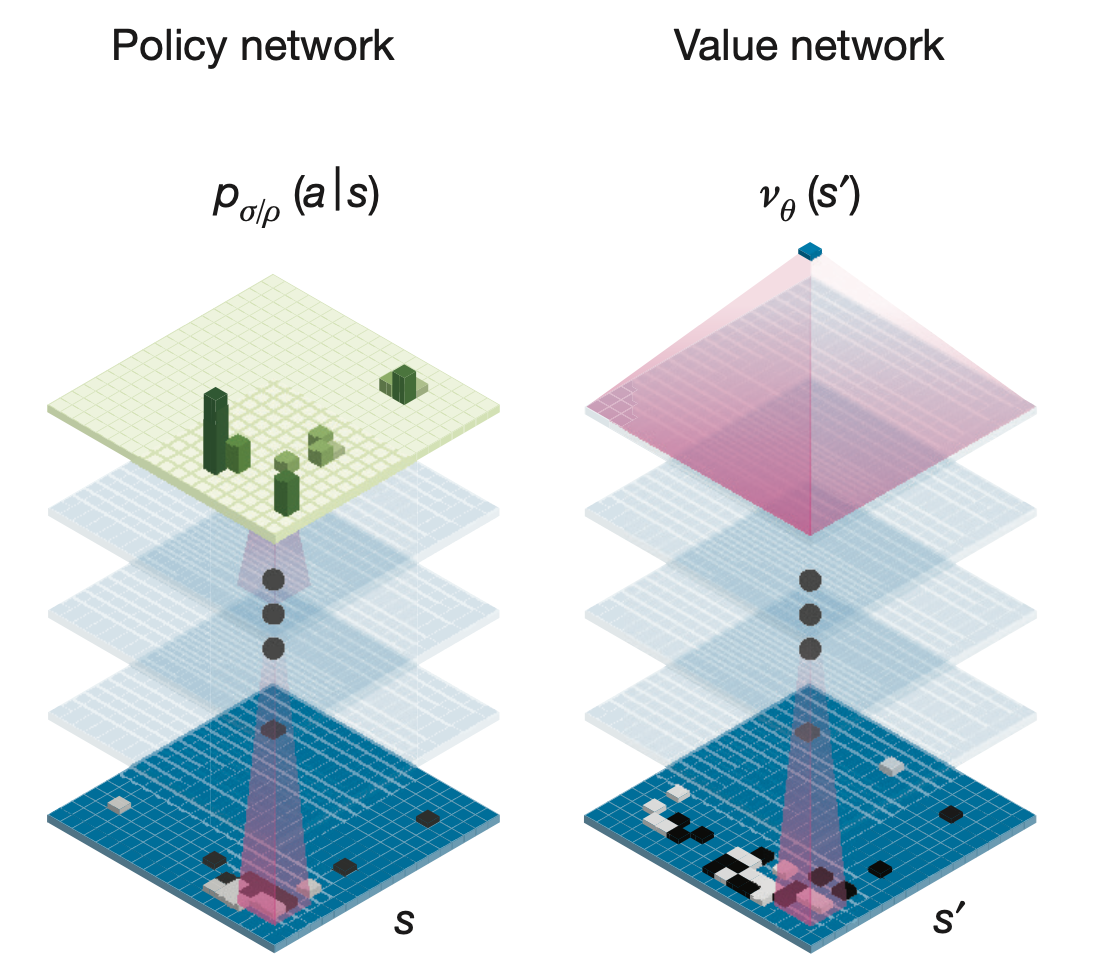 Fig. 2 Networks of AlphaGO.
Fig. 2 Networks of AlphaGO.
학습은 이렇게 했다고 치고 그럼 어떻게 실제 학습된 network로 바둑을 둘까요? 바둑판의 상태 \(s_t\)를 주면 우리는 그 다음 action, \(a_t\)의 확률 분포를 알려주는 네트워크가 있으니 이 중에서 가장 큰 확률을 가지는 수를 두면 될까요? 답은 아닌데요, 논문 제목에서도 알 수 있듯 실제 이세돌 9단이나 판 후이 9단과 바둑을 둘 때 AlphaGO는 꽤 복잡한 process를 거쳐서 둘 수를 결정합니다.
아래의 figure를 보시면 AlphaGO가 얻을 수 있는 여러가지 정보들이 있는데, 그 중 value network 값이 있습니다.
이는 현재 \(s_t\)에서 policy를 따라 둘 수 있는 다음 수 들 중에서 실제로 그 수를 둬서 \(s_{t+1}\)이 되었을 때 \(V(s_{t+1})\)을 의미합니다.
그런데 바둑의 return 값은 게임을 끝까지 뒀을 때 이기면 +1점 지면 0점입니다.
그러니까 \(V(s_{t+1})\)도 그 사이 어느 값을 의미하게 되는데 이 것은 직관적으로 승률과 같다고 할 수 있습니다 (0~1 사이 값).
여기서 굉장히 중요한 insight는 내가 현재 이 수를 뒀을 때 승률이 얼마나 떨어지는가?를 value network로 알 수 있으므로, 우리는 바둑을 둘 때 policy network가 주는 확률 분포중에서 가장 높은 값을 의미하는 action을 고르는게 아니라, 가능한 수 ( < 19x19(바둑판 크기))를 한번 다 둬 보고 그 때 그 다음 상태의 승률이 가장 높은 action을 취하는 방법으로도 action을 고를 수 있습니다.
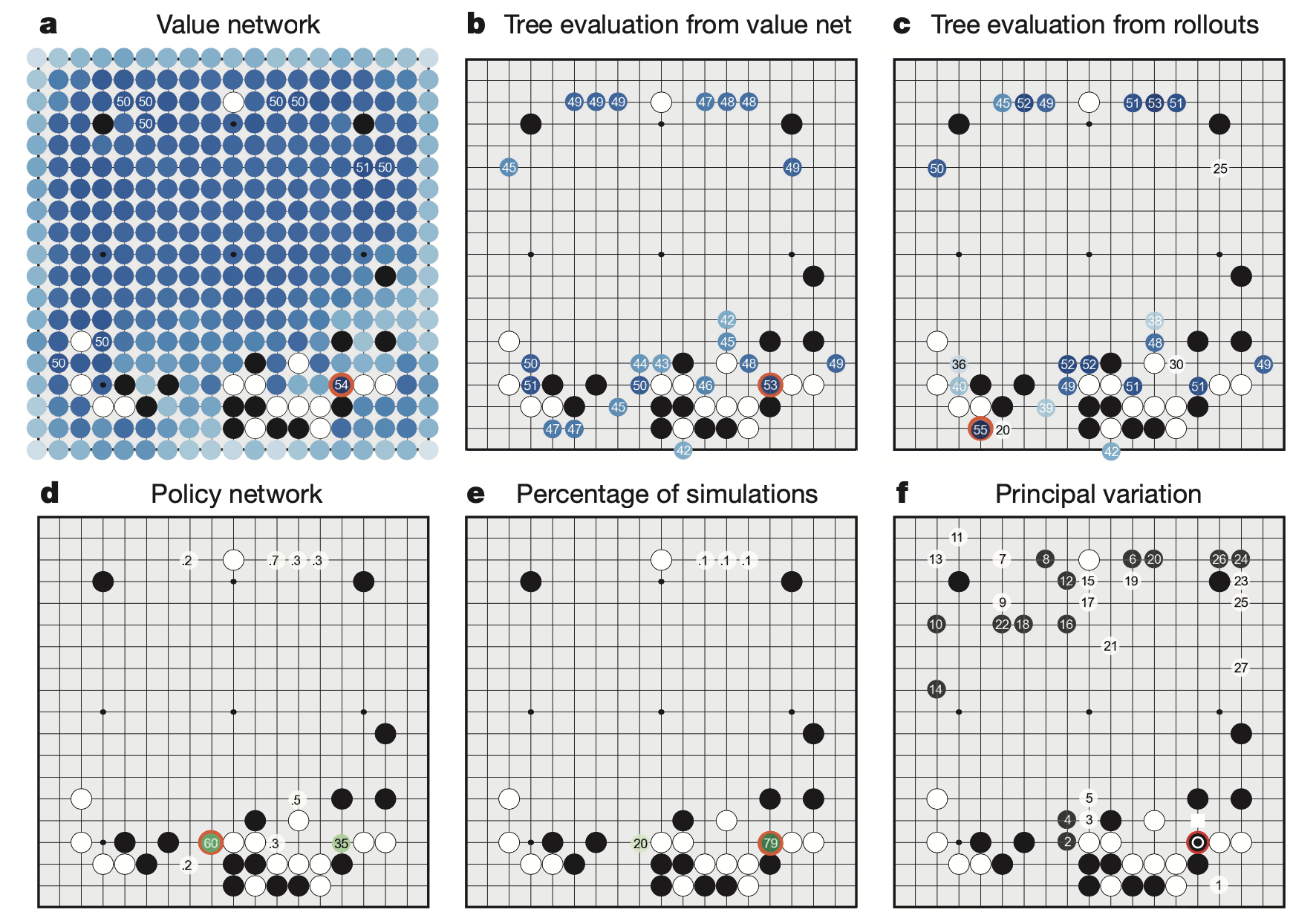 Fig. How AlphaGo (black, to play) selected its move in an informal game against Fan Hui.
Fig. How AlphaGo (black, to play) selected its move in an informal game against Fan Hui.
하지만 실제 AlphaGO는 위의 여러가지 policy network가 주는 action들의 확률, 실제 그 수를 뒀을때 value network가 주는 승률, 여러번 수를 둬보는 simulation을 했다고 쳤을 때 (나중에 planning이라는 이름으로 chapter 또 있습니다) 그 state를 방문한 횟수 등을 모두 고려한 Monte Carlo Tree Search (MCTS)를 통해서 수를 두게 되는데, 이는 굉장히 복잡하므로 나중에 따로 다루도록 하겠습니다.
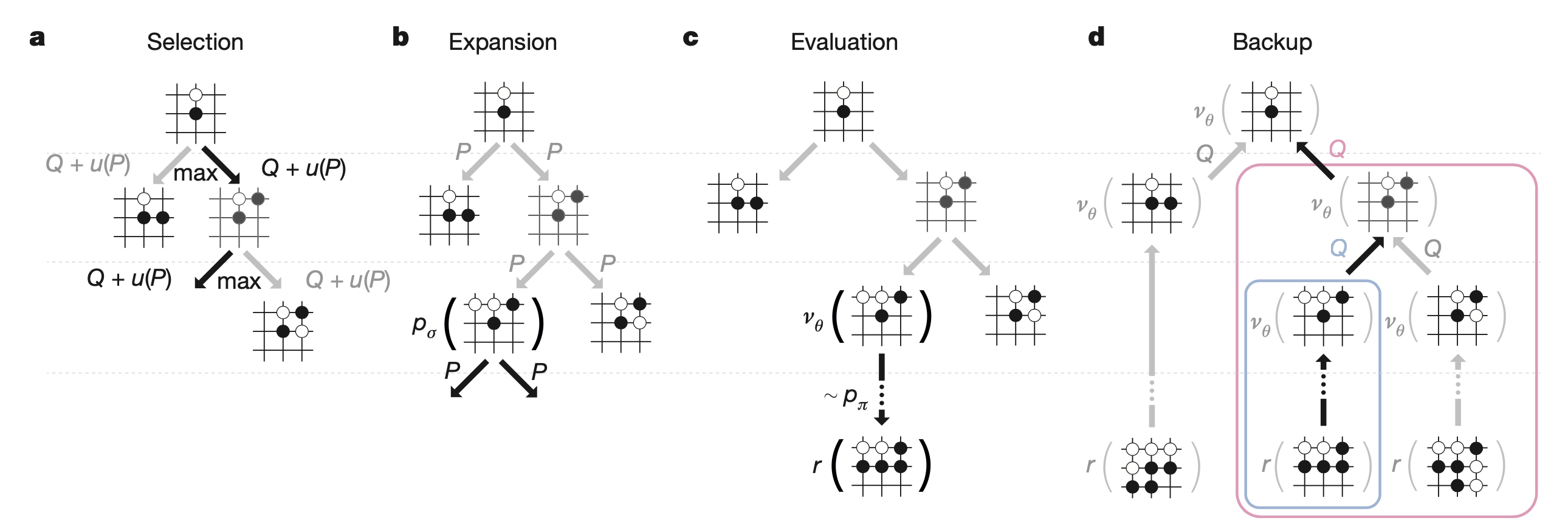 Fig. Monte Carlo tree search in AlphaGo.
Fig. Monte Carlo tree search in AlphaGo.
중요한 점은 V를 계산하는 것, 즉 policy evaluation이라는 것이 이런식으로도 해석이 될 수 있다는 점이며,
추가로 덧붙혀서 누군가 바둑의 존재 가능한 경우의 수는 우주에 존재하는 원자의 수와 같아서 학습할 수 없다는 점을 Deep RL로 학습했다는 것이 굉장히 시사하는 바가 크다는 겁니다.
아까 말씀드린 것 처럼 우리는 Critic (Value) Network라는 것이 있으므로 가능한 모든 수를 탐색하고 거기에 점수를 매길 필요가 전혀 없어진 셈이 되거든요.
Additional Bellman Equation
왜인지모르겠으나 cs285에서는 Sergey가 Bellman Equation에 대해 설명하지 않습니다. 설명을 안했다는건 아닌데, 굳이 bellman equation이라는 RL에서 매우 중요한 terminology를 언급하지 않습니다. 앞서 Q, V를 current reward + next state에서의 Q or V로 표현하는 것이 있었는데, 이걸 bellman equation이라고 합니다.
먼저 V에 대한 Bellman Equation은 매우 자명합니다. 아래처럼 현재 timestep의 state에서 그 다음 transition가능한 state에서의 reward를 weighted sum하는 것을 반복하는겁니다.
 Fig.
Fig.
위의 slide의 equation에서 즉시 현재 state에서 가능한 action들을 통해 얻을 수 있는 current reward (혹은 immediate reward)는 \(R_{t+1}\)로 가능한 action을 다 해보면 environment가 주는 값이므로 expectation의 밖으로 나와도 됩니다.
 Fig.
Fig.
그 다음은 state action value function, Q 에 대한 bellman equation입니다. Q또한 마찬가지로 decomposition을 할 수 있는데,
 Fig.
Fig.
이는 아래처럼 다양한 형태로 나타낼 수 있습니다. (다 배운 내용입니다)
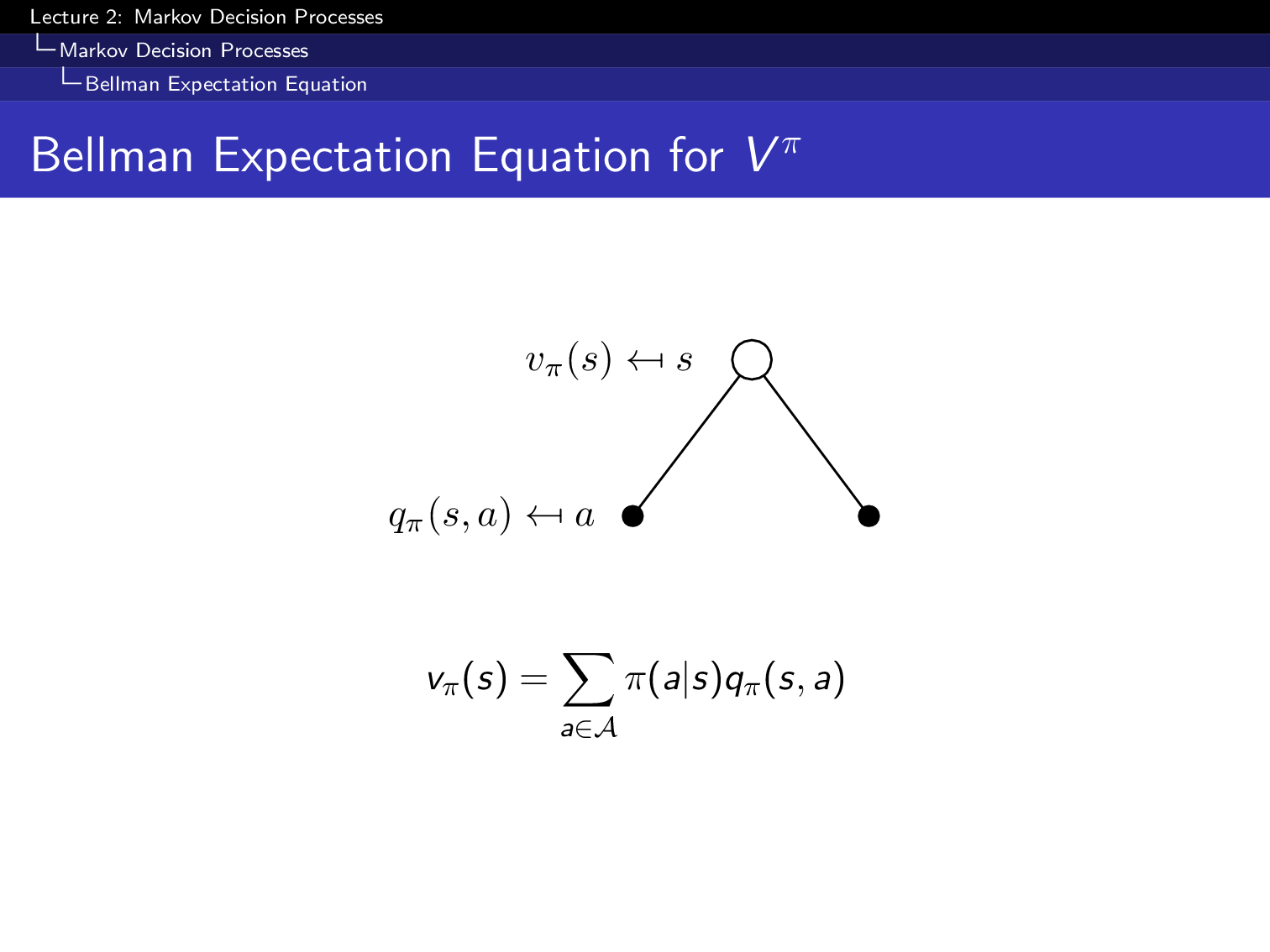 Fig.
Fig.
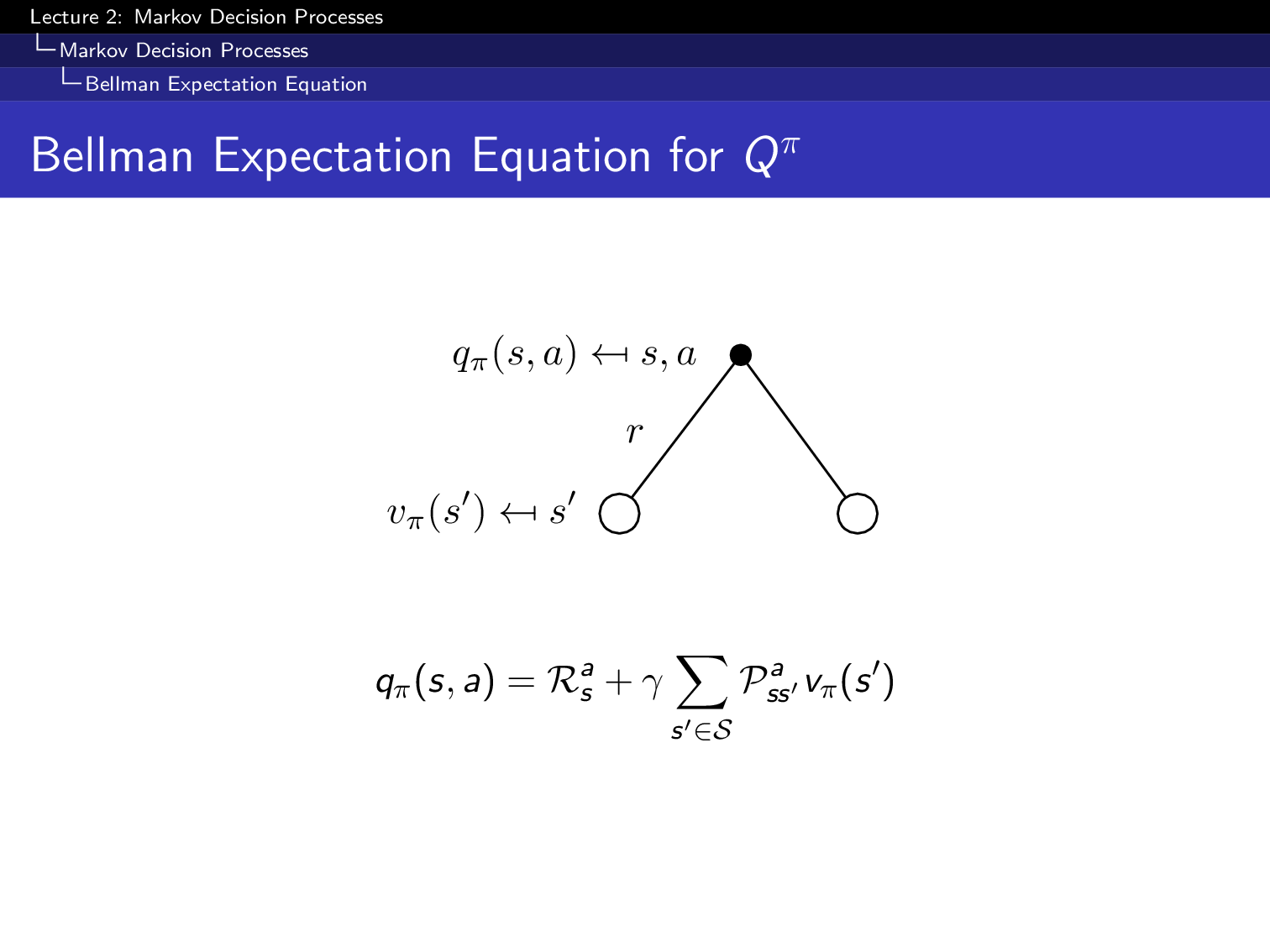 Fig.
Fig.
 Fig.
Fig.
 Fig.
Fig.
From Policy Evaluation to Actor Critic
다시 강의로 돌아오겠습니다.
 Slide. 12.
Slide. 12.
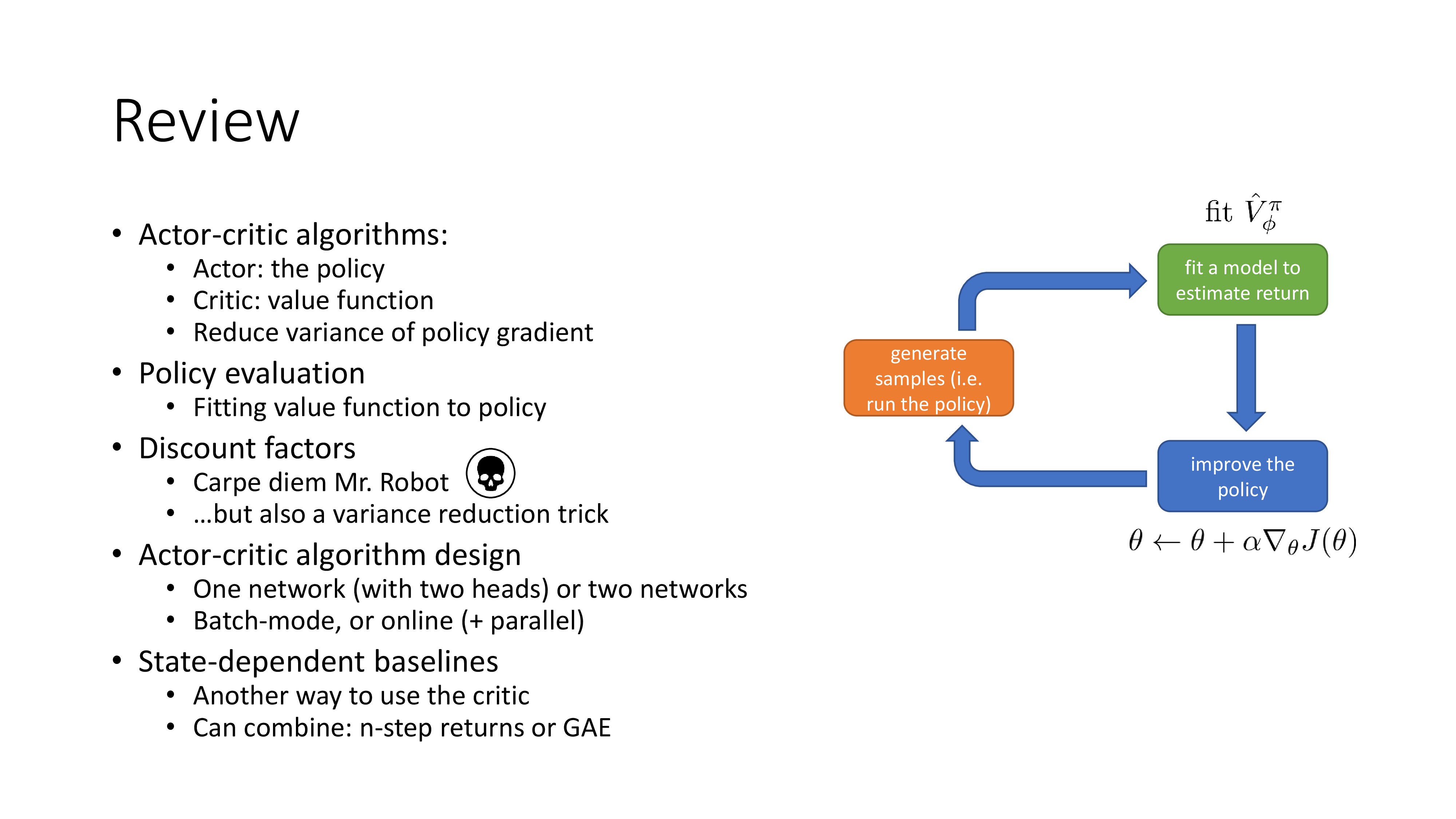
Actor-Critic algorithm의 기본적인 batch는 위와 같이 구성되어 있는데요,
근본적으로 앞서 배운 VPG인 REINFORCE와 크게 다르지 않습니다.
- rollout 해서 trajectory 샘플을 여러 개 만든다.
- 각 state, action에 대해서 그 action을 했을 때의 reward sum을 계산한고 (single sampling estimator or bootstrapped), 이를 target으로 NN, \(\hat{V}^{\pi}_{\phi}(s)\)를
Critic을 학습(update) 한다. - 각 state, action에 대해 Adavantage, \(\hat{A}^{\pi}(s_i,a_i)\)를 계산한다.
- 얻은 \(\hat{A}^{\pi}(s_i,a_i)\)를 통해서 objective의 gradient를 구한다.
Actor를 학습(update) 한다.
여기서 다시 한 번 확실히 짚고 넘어가야 되는것은
- 우리는 network가 2개 있다. (\(\pi, \phi\))
- 한 iteration에 Critic update, Actor update를 번갈 아가면서 한 번씩 한다.
입니다.
Discount Factor
그 다음으로 알아볼것은 Discount Factor입니다.
앞선 post에서 제가 reward, return 개념을 설명드리면서 짧게 언급했었습니다.
 Slide. 13.
Slide. 13.
우리가 해결하고자 하는 것은 만약 terminal state가 존재하지 않는 infinite horizon case일 경우 어떻게 학습을 할 것이냐? 입니다.
만약 \(T \rightarrow \infty\)라면 critic이 target하려는 값이 무한대에 가까워 지면서 학습을 할 수 없게 됩니다.
이는 slide에 나와있는 예시로는 최대한 오랫동안 걷는 agent를 만든다거나 할 때를 말합니다.
이를 해결할 수 있는 가장 단순한 해결책은 바로 \(\gamma \in [0,1]\)라는 discount factor를 도입하는 겁니다.
\[\begin{aligned} & y_{i,t} \approx r(s_{i,t},a_{i,t}) + \hat{V}_{\phi}^{\pi}(s_{i,t+1}) & \\ & y_{i,t} \approx r(s_{i,t},a_{i,t}) + \gamma \hat{V}_{\phi}^{\pi}(s_{i,t+1}) & \\ \end{aligned}\]이름에서도 알 수 있듯, 할인해주는 factor 입니다. 어떤 rule에 따라 할인을 해 주냐 하면, 내가 현재 평가하려는 t step 에서 멀어질수록 할인율을 크게 적용해서 멀리 떨어진 (무한히) 경우에 대해서는 reward를 0으로 주는 것이죠.
사실 강화학습에서 discount factor에 대한 얘기는 많은 서적에서 제일 앞부분에 등장해서 강화학습 책을 한번이라도 접해보신 분들에게는 익숙하실텐데요, 이는 강화학습이 미래의 reward들 까지 다 고려해서 행동을 한다고 하지만, 그래도 현재 받는 reward에 가장 높은 weight을 부여해서 미래의 reward도 고려할거긴 하지만 그래도 현재의 action이 초래한 reward가 더 중요하니 이걸 기준으로 action을 평가하겠다라는 의미로 해석하곤 합니다.
이러한 discount factor를 도입하는 것은 MDP의 결과를 바꾸기도 한다고 하는데요, 사실 이 부분이 이해가 조금 어려우실 수 있습니다. slide의 그림을 같이 보고 이해를 해 봅시다. 원래는 death라는 state가 없고 4개의 state만 있었습니다.
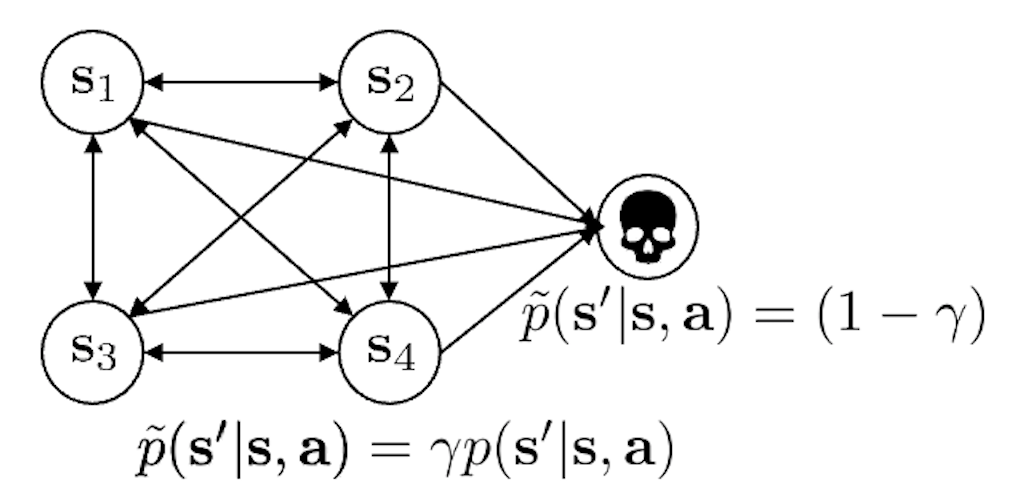
MDP확률에 따라 transition이 일어나게 될 텐데, \(\gamma\)를 도입한다는 것은 4개의 원래 state에서 들어가면 절대 빠져나올 수 없는 개미지옥같은 death state로 갈 확률이 \((1-\gamma)\)가 되는 death state를 추가하는 것과 동치가 된다고 합니다. 전체 확률의 합은 1이어야 함으로 원래 transition 확률은 \(\gamma\)만큼 보정 (discount)을 받아야 겠죠? 이 death state에 빠지면 영원히 빠져나올 수 없게 되어 최종적으로 받게되는 reward가 0이라고 합시다.
이제 어떤 state에서 action을 해서 그 다음 state로 갈 수 있는 가능성이 \(s_3\)입장에서는 어떤 action을 함으로써 갈 수 있는 다음 state로 \(s_1, s_2, s_4\) 외에 \(s_{death}\)가 추가되어, 언제든 죽을 확률이 생겼으므로 내가 나중에 할 action은 그렇게 중요하지 않다, 즉 현재의 action이 더 중요하다는 의미를 가지게 됩니다.
Gamma값에 따라서 \(\gamma=0\)이면 현재의 reward만 보고 사는 agent, 즉 오늘만 사는 agent가 되는것이며 \(\gamma=1\)이면 미래에 끼칠 영향을 엄청 챙기면서 행동하는 것이 되고, \(\gamma=0.9 \sim 1\)정도면 적당히 생각하는 것이 됩니다.
어쨌든 이 discount factor를 몬테 카를로 방법을 사용하는 일반적인 VPG에 적용해 보겠습니다.
 Slide. 14.
Slide. 14.
Slide. 14.의 수식을 보시면 option이 2가지가 있다는 걸 알 수 있습니다.
Option 1은 t시점의 action의 reward을 \(t\)시점부터 보는 원래의 causality가 적용된 수식이며, discount도 \(t'=t\) 기준으로 적용이 됩니다.
Option2는 “음 내가 그래도 t=0부터 action을 했으니까 discount도 t=0부터 한걸 계속 적용하겠다”가 됩니다.
Option2의 form에 option1에서와 같이 causality를 적용하고 싶습니다.
그러면 3,4번째 수식이 되는데, 보시면 grad log probdp \(\gamma^{t-1}\)이 붙어있는 걸 보실 수 있습니다.
이는 episode초기의 action을 더 중요하게 생각해서 더 많이 update 하겠다 는 의미를 내포하게 됩니다.
Option 1에서의 log prob에 붙은 quantity의 의미는 가까운 시일의 action이 초래한 reward가 더 값지다라는 의미로 살짝 두개는 다르다고 볼 수 있습니다.
Option 2는 이 2가지 철학이 모두 들어갔다고 할 수 있죠.
여기서 어떤 option이 더 나은지는 아래의 슬라이드에 답으로 나와있습니다.
 Slide. 15.
Slide. 15.
실제 학습을 할 때는 대부분 option1을 쓰는데, 그 이유는 미래의 action이 안중요한 것은 아니기 때문입니다. Early step뿐만 아니라 later step의 action들도 잘 했으면 하는겁니다.
그리고 추가적으로 discount factor를 추가하는 것이 infinite horizon만을 위한 것은 아닙니다. 이는 variance 또한 줄여준다고 하는데요, 우리가 trajectory를 sampling할 때 timestep이 경과될수록 variance가 커지는데 timestep이 경과될수록 이것의 영향력을 줄이기 때문인 것 같습니다.
 Slide. 16.
Slide. 16.
이제 마지막으로 discount factor까지 적용한 Actor-Critic Algorithm의 batch에 대해서 얘기하고 subsection을 마치겠습니다.
Discount factor가 적용된 부분은 step 3가 되겠습니다.
그리고 Slide. 16.에는 Online Actor-Critic Algorithm이 있는데요, 이는 Infinite horizon case에 대해서 적용하기 위한 algorithm이라고 합니다.
자세히 보시면 변수에 subscript i 가 더 이상 없습니다.
이는 trajectory를 다 뽑아두고 학습하는 Eposodic case처럼 할 수 없기 때문에 \(s_t\)에서 \(a_t\)을하면 바로 다음 \(s_{t+1}\)로 가고, reward, \(r_t\)를 받고… 딱 이 4가지 tuple만 가지고 업데이트를 하는 겁니다.
- 4~6장 까지
variance 줄이는 방법Summary- baseline 도입
- critic 도입하기
- discount factor
Actor-Critic Design Decisions
NN Architecture decision for Actor-Critic
이제 Actor-Critic algorithm을 사용하기 위한 조금 practical한 테크닉들을 알아보도록 하겠습니다.
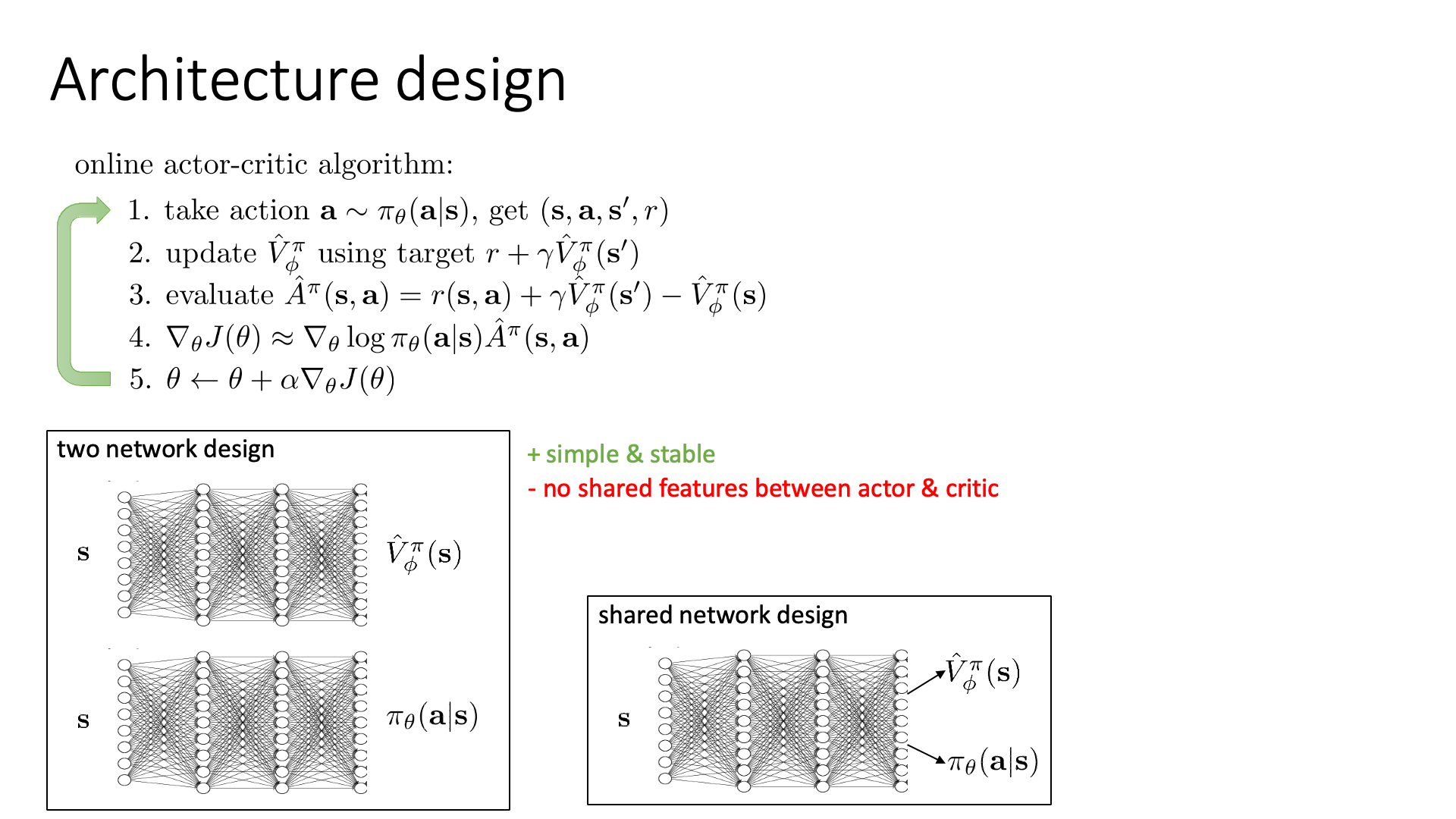 Slide. 18.
Slide. 18.
우선 Vanilla Policy Gradient 방법론은 뉴럴 네트워크 하나가 policy를 모델링하기 때문에 굉장히 명확했는데요,
Actor-Critic은 지금 policy와 Value function 두 가지를 다 모델링 해야 하는 상황입니다.
가장 심플한 방법은 Slide. 18.의 좌하단 그림처럼 네트워크를 두개를 두는 겁니다. (각각 파라메터 \(\phi,\pi\)로 구성됨)
하지만 이렇게 할 경우 두 네트워크가 서로 feature (representation)을 공유하는 일이 없다는 단점이 있습니다.
그렇기 때문에 또 다른 방법으로는 shared network를 두고 최종 출력 직전의 디코더만 두 개로 구성하는 것이 있습니다.
이렇게 되면 internal representation을 공유하기 때문에 학습하기 더욱 용이할 수 있다고 합니다.
이는 머리가 두개 달린 용? hydra 같다고 하여 hydra 구조라고도 합니다.
하지만 이렇게 이론적으로 작용할것 처럼 보이는 두 번째 방법론도, 학습이 unstable하게 되는 문제가 있다고 하는데요, 왜냐하면 이는 소위 말하는 Multi-task Learning과 유사한 방법론인데, 이런 Multi-task Learning 에서는 두 task의 난이도가 다를 경우 적절하게 weight를 주지 않고 학습하게 되면 문제가 생기기 마련이기 (heuristic하게 하이퍼 파라메터를 정해야겠죠) 때문일 수도 있습니다.
혹은 Phasic Policy Gradient같은 paper에서 말 하는 것 처럼 shared 구조를 사용할 경우 optimization 관점에서 서로 간섭이 생겨서, 잘 학습이 되지 않는 문제가 발생할 수도 있습니다. Analyzing the Sensitivity to Policy-Value Decoupling in Deep Reinforcement Learning Generalization같은 paper에서는 sharing을 하는것이 과연 실제로 좋은가? 안좋으면 왜안좋고, 만약 network가 20층 정도 된다면 10층까지는 sharing을 하는게 더 좋은지? 어디까지 sharing하는것이 좋은지?등에 대한 연구 결과를 보이기도 했습니다.
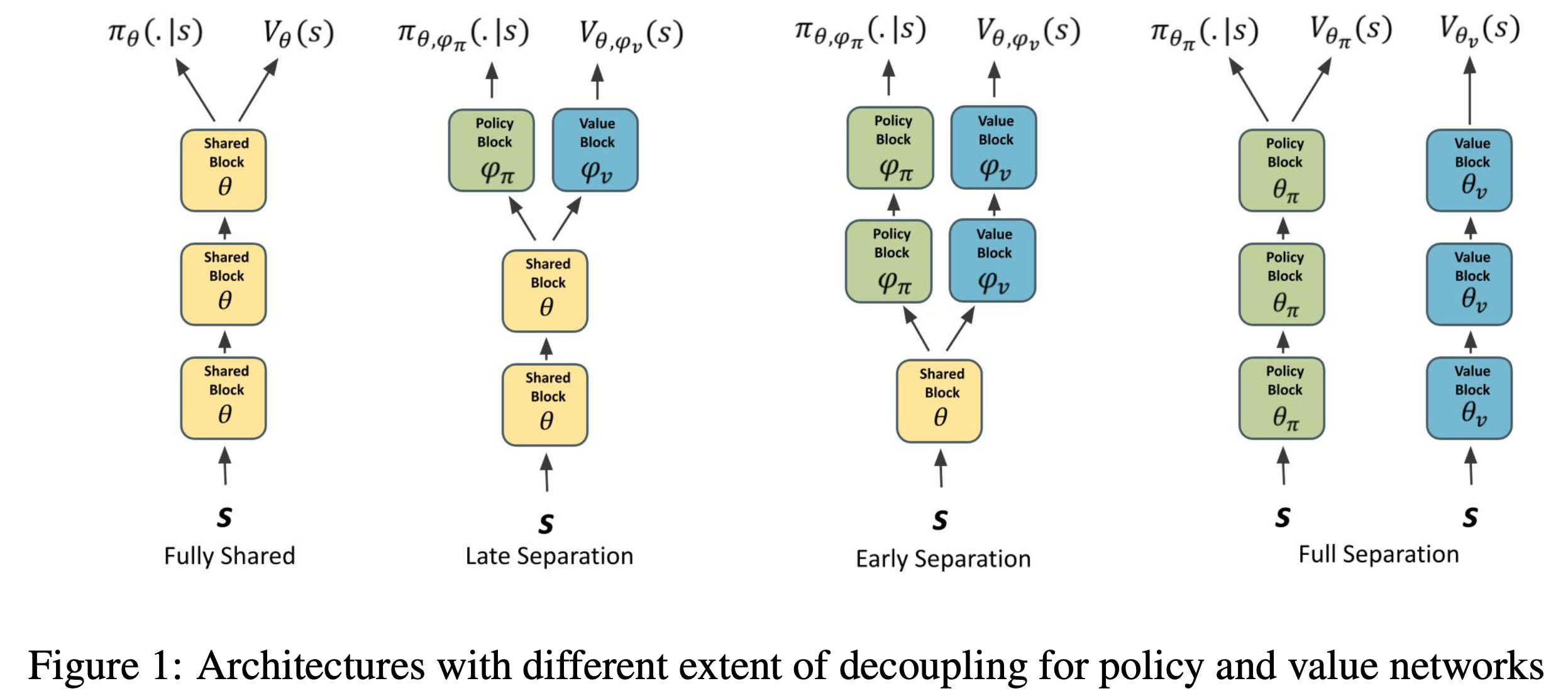 Fig.
Fig.
Parallel Actor-Critic
앞서 소개했던 Online Actor-Critic 방법은 1번 sampling해서 policy, value network를 각각 바로 업데이트 하는 데 사용하는 1 batch approach였습니다.
(trajectory를 여러 개 sampling 한 것이 아님)
 Slide. 19.
Slide. 19.
이는 variance가 줄어들긴 했으나 여전히 high variance 하기 때문에 가지고 있기 때문에 Deep RL algorithm들에서 좋지 않은 성능을 보인다고 합니다.
Online Gradient Descent (Stochastic GD, SGD)로 최적화를 하는건 일반적인 지도학습 방법론을 사용하는 딥러닝 네트워크들에서도 좋지 않는 성능을 보이기 때문에 Deep RL에서는 더한것이죠.
그래서 제안된 것이 매 번 policy와 value function을 업데이트하지 말고 모아서 업데이트 하는 겁니다. 하지만 이러한 방법도 마냥 좋지는 않은데 그 이유는 여러 번 sampling해서 업데이트를 하려고 해도 sample들이 다 비슷할거기 때문이라고 합니다 (highly correlated). 그니까 지금 본 state, \(s_t\)와 다음 state, \(s_{t+1}\)랑 굉장히 비슷할 거라는 겁니다.
이를 해결하기 위한 좋은 방법으로 Parallel Worker를 사용하는 방법이 제안되었다고 합니다.
이는 Synchronized Parallel Actor-Critic Algorithm을 디자인 하는것으로 아래의 그림을 보시면 이해가 빠릅니다.
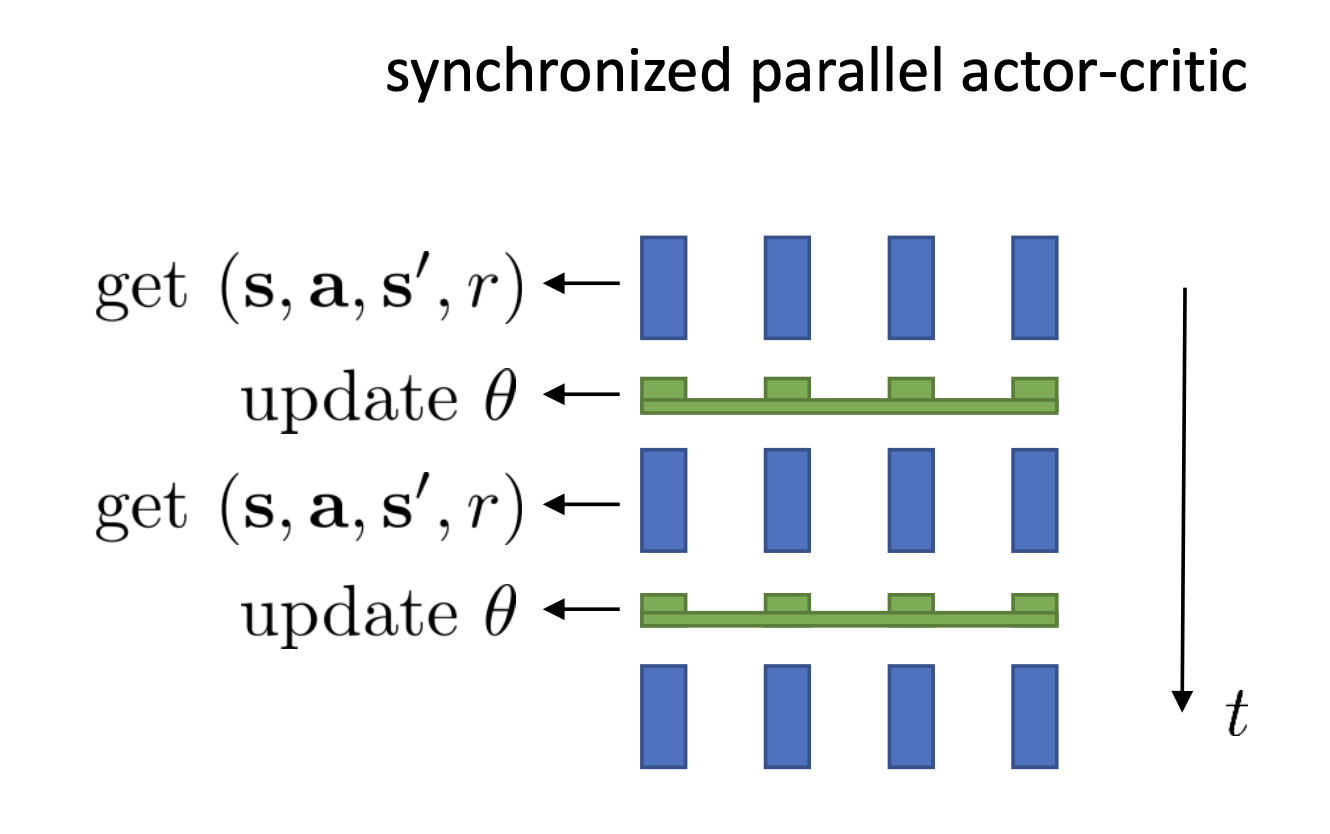
위의 그림을 보시면 worker가 4개이고 4개는 각기 다른 랜덤 시드를 가질것이기 때문에 매우 다른 상황에 놓여 있을 겁니다. 이런 샘플들을 모아서 하나의 큰 배치로 생각하고 모든 업데이트가 끝날 때 까지 기다린 다음 다시 또 진행하고 모으고 가치,정책 업데이트하고 …를 반복하는 겁니다. 한 worker내에서는 이 전의 gradient와 correlation이 있겠으나 다른 worker들끼리는 서로 관련 없는 독립 (independent)이기 때문에 상관이 없다고 합니다.
하지만 우리가 굉장히 많은 worker pool을 가지고 있는 경우는 어떻게 할까요?
또 다른 방법은 바로 비동기화 된 (Asynchronized) algorithm을 디자인 하는 겁니다.
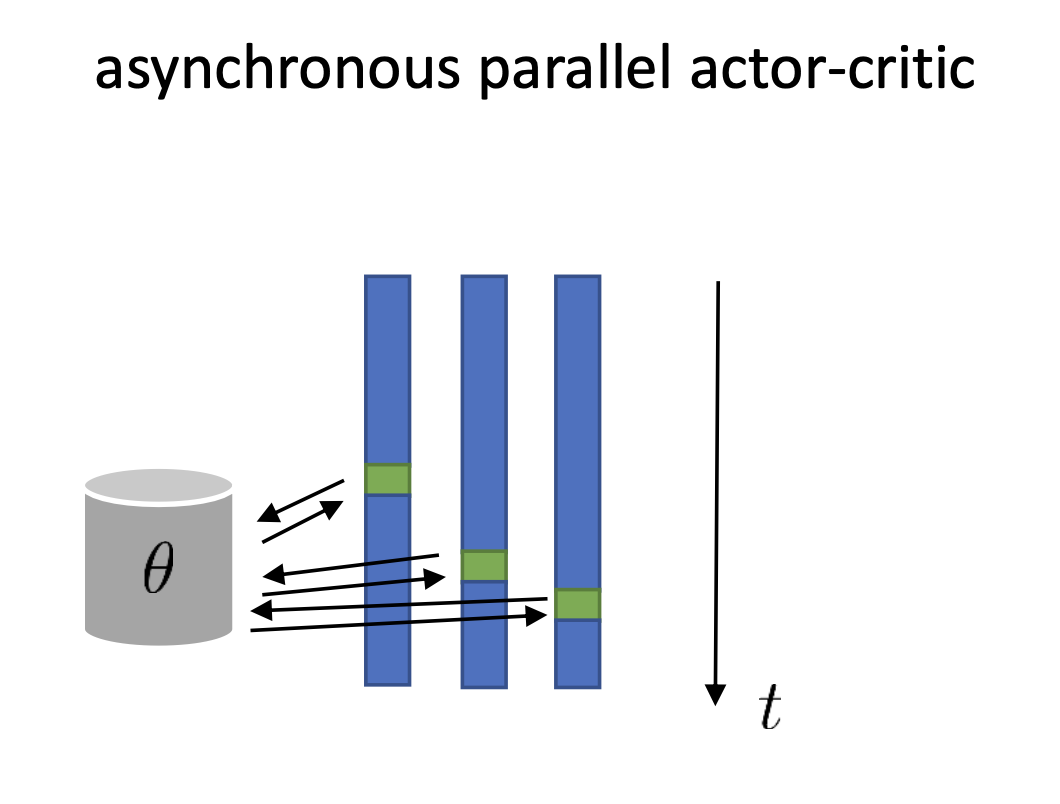
이 algorithm이 위와 다른 것은 central parameter가 worker가 sampling한 데이터들을 기반으로 업데이트가 되고, worker들이 기다리지 않으면서 계속 샘플을 하며 전진한다는 겁니다. 그림을 보시면 latest parameter를 관리하는 메모리가 하나 있고, rollout을 하는 worker들이 데이터가 만들어지는 족족 parameter를 update하고 있습니다. 그렇다면 어떤 process는 t=10 의 parameter를 가지고 rollout을 하는 중에 다른 worker들이 이미 t=11,12로 update를 하기 때문에 10번째 policy로 만든 data tuple로 13번째 parameter를 만들어야 하는 상황과 마주할 수 있습니다. 과연 이렇게 해도 수학적으로 동치인 PG를 하는 것이 될까요?
당연히 아닙니다. 수학적으로 동치가 아닐 뿐더러 이는 앞서 살짝 언급되었던 off-policy가 되는 것과 다름 없습니다.
즉 행동한 (rollout한) policy와 update하려는 policy가 다른거죠.
우리가 앞서 논한 PG들은 다 on-policy인 것을 가정하고 생각한건데 이치에 맞지 않습니다.
하지만 이는 최신 (latest) policy와 조금 behavior policy의 격차가 그리 크지 않기때문에 수학적으로는 동치가 아니지만 그럼에도 불구하고 실제로는 잘 작동한다고 합니다.
이러한 비동기식 (asynchronous ; 동시에 발생하지 않는) algorithm은 2016년에 제안된 Deepmind의 논문 Asynchronous Methods for Deep Reinforcement Learning 에서 제안되었으며 Asynchronous Advantage Actor-Critic (A3C)이라고 불리웁니다.
(내용이 더 궁금하신 분들은 직접 paper를 찾아보시면 좋을 것 같은데, paper에서는 policy based가 아닌 value based에 asynchronous manner를 쓴 것 같습니다. 일단 한 번 맛만 보시고 다음 7, 8장의 value-based chapter에서 다시 보시는 것이 어떨까 싶습니다.)
이는 우리가 large scale deep learning을 하기 위한 분산 학습 (distributed training)을 할 때의 경우와도 관련지어 생각할 수 있습니다. Data Parallel (DP)을 할 때 한 process가 다른 process의 forward-backward를 기다리는 동안 아무것도 할 수 없기 때문에 만약 batch구성이 좋지 않게 되어 어떤 process 하나만 큰 batch를 받게 되면 다른 worker들은 모두 이를 기다려야 하므로 병목이 생길 수 있습니다.
그리고 A3C는 사실 timestep 단위로 async학습을 하는건 아닙니다. 실제로는 바둑을 두는 agent를 학습한다고 할 때 각 episode가 끝나는 시점이 어떤 worker는 n=180, 어떤 worker는 n=150 이럴 수 있기 때문에 꽤 timestep이 차이나는 경우에 대해서 async하게 update를 한다고 합니다. (이래도 괜찮다는거 같네요)
Off-Policy Actor-Critic
(이 subsection은 Fall 2021 이상의 강의에서만 들을 수 있으니 CS285 2020들으시는 분들은 유의해주세요.)
그런데 online A2C를 학습할 수 있는 또 다른 방법이 있습니다.
단순히 asyncronous하게 학습해서 약간 오래된 state, action을 쓰는 것이 아니라 엄청 오래된 state, action 들도 쓰는건 어떨까? 에서 출발합니다.
당연히 state, action 등 \((s,a,s',r)\) tuple을 sampling 해야 하긴 하지만 replay buffer라는 곳에 계속 쌓아두면서 random 하게 batch 단위로 꺼내서 policy를 학습하는 개녑입니다.
시간이 지나면서 replay buffer에는 엄청난 tuple set이 쌓일테고 queue구조로 해서 fixed length를 넘어가면 먼저 쌓였던 tuple은 버린다던가 해도 됩니다.
이런 방식이 바로 off-policy Actor-Critic입니다.
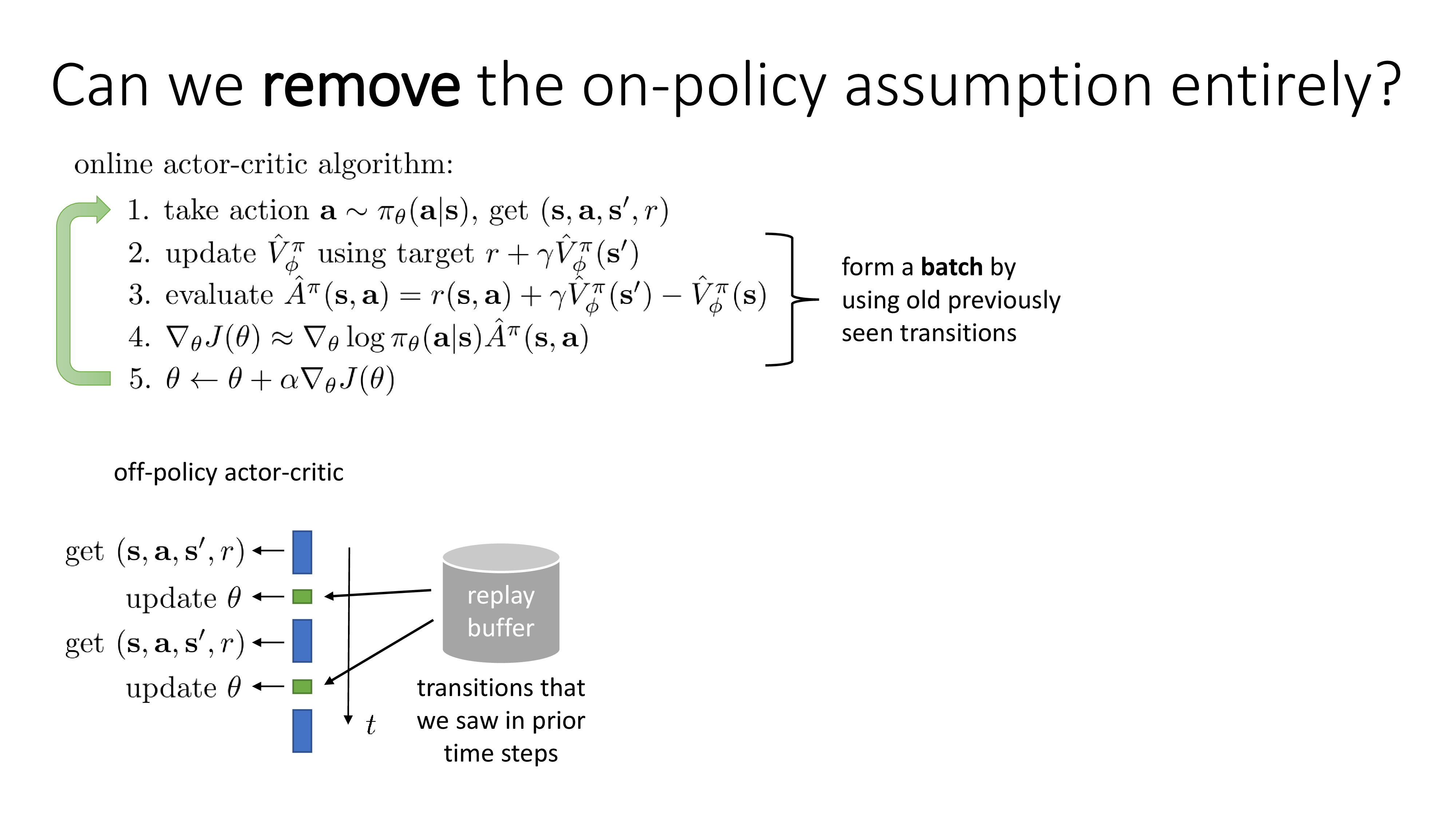 Slide. 20.
Slide. 20.
그런데 이렇 학습을 하면 policy가 망가진다고 합니다. 왜냐하면 Critic을 학습하기 위한 target과 Actor를 업데이트하는 gradient 수식에서도 log prob이 잘못됐기 때문입니다. (아마 수학적으로 문제가 있고 이상한 target을 따라가다보니 수렴자체를 안하고 이상한 policy로 계속 남아있게 된다는 말 같습니다)
 Slide. 21.
Slide. 21.
한 번 생각해봅시다. 위의 slide는 여태까지 배운 Actor-Critic을 off-policy manner로 수정한 것입니다. 어떤게 잘못 됐을까요?
Main idea는 내가 뽑은 transition sample이 current policy가 아닌 old policy 에 의해 결정된 것이다라는 겁니다.
Critic에 대해서 먼저 생각해봅시다. Critic의 target은 원래 ideal target을 써야하는데 expectation을 정확히 구할 수 없으니까 boostrapped target을 쓰는거였습니다. 그런데 ideal target은 실제로는 아래와 같이 생겼죠.
\[V_{\phi}^{\color{red}{\pi}}(s_t) = \sum_{t'=t}^{T} \mathbb{E}_{\color{red}{\pi_{\theta}}} [r(s_{t'},a_{t'}) \vert s_t] = r(s_t, a_t) + V_{\phi}^{\pi}(s'_{t+1})\]즉 \(V\)는 어떤 state에서의 reward값의 합의 expectation인데, 여기서 중요한 것은 V는 current policy를 따를 때의 expectation 이라는 겁니다.
우리가 뽑은 tuple이 아주 초기 policy로 sampling한 (old policy) \(s_0,a_0,r_0,s'_0\)라고 생각해 봅시다.
그런데 만약 policy가 계속 학습돼서 현재 policy는 과거와 많이 달라졌습니다.
그러니까 더이상 해당 \(s\)에서 \(a\)할 확률이 작아서 이런 action을 할 일이 없는거죠.
그러니까 자연스럽게 이 그 다음 state인 \(s'\)도 틀린게 됩니다.
따라서 \(V(s_0)\)의 approximate한 target 값으로 \(r_0 + \gamma V(s'_0)\)을 쓰는건 잘못된거죠.
만약 이 action을 할 확률이 계속 높게 유지되었다면 expectation을 이 action이 가져다줄 return으로 approximate한 것은 문제가 없었을 겁니다만 그게 아니죠.
Actor에서의 문제도 비슷한데, 우리가 policy gradient를 계산할 때 매우 매우 중요했던 것 중 하나는 이 action은 current policy를 따라서 sampling된다 라는 것이었습니다.
예를 들어 policy가 구릴 적에 \(s_i\)에서 \(a_i\)를 할 확률이 0.4 였다고 생각해 봅시다.
그런데 그건 형편없는 policy를 따랐을 때고, policy가 개선이 되면서 이제는 \(s_i\)에서는 \(a_i\)를 확률이 0.05로 줄었다고 칩시다.
현재 policy를 기준으로 생각하면 더 이상 이런 action은 할 리가 없는데도 계속 이 action을 평가하고 이 action의 확률값을 조정하는 일을 해야 된다는 겁니다 (not the action current policy would have taken !).
이럴 경우 앞선 lecture에서 배운 것 처럼 importance sampling을 해서 확률값을 보정 해줘는 방법으로도 해결할 수 있겠으나 이번에는 다른 방법을 알아볼 것입니다.
(추가로 더 좋은 방법이 있다고 하는데, 아마도 본인이 쓴 off-policy Actor-Critic 중 standard인 Soft Actor-Critic (SAC)를 말하는 것 같습니다만 그 방법은 나중에 알려준다고 합니다.)
우선 3번 Value Function의 target부터 고쳐봅시다.
Sergey가 제안한 해결책은 바로 V대신 Q를 쓰자는 것 입니다.
 Slide. 22.
Slide. 22.
이것은 굉장히 말이 되는 해결책인데, 우리가 문제점으로 지적한 것은 어떤 state의 value, \(V(s) = \mathbb{E}\)를 대표하는 값으로 이상한 action을 쓴다는 거였는데, 그냥 Q를 학습하면 이럴일이 없는겁니다. (V=Q를 평균)
그럼 Critic은 이제 state-action 두 개에 dependent한 \(Q(s,a)\)를 쓸거고 이거의 target은
\[r_i + \gamma \hat{Q}_{\phi}^{\pi} (s'_i, a'_i)\]가 됩니다. 이제 replay buffer에서 sampling한 \(s_i,a_i,r_i,s'_i\)를 가지고 그 state에서 그 action 을 했을 때의 값을 학습하는 것이니까 아무런 문제가 없죠? 이렇게 target을 바꿈으로써 하나 문제가 되는 것이 있다면 buffer에 \(s'_i\)는 있지만 \(\color{red}{a'_i}\)가 없다는 문제가 있습니다. 근데 이것은 간단하게 구할 수 있는 것이 current policy에 \(s'\)를 넣으면 별다른 과정 없이 바로 알 수 있기 때문입니다 (\(\pi( \cdot \vert s_t')\)). 이건 sampling 과정도 아닙니다.
그 다음은 Actor 쪽의 gradient 계산하는 부분을 봅시다.
 Slide. 23.
Slide. 23.
더이상 current policy는 buffer속의 오래된 transition tuple, \(s,a,r,s'\)의 action을 할 가능성이 없을 수 있습니다. 그러니까 i번째 transition에 대해서
\[\log \pi_{\theta} ( a_i \vert s_i)\]의 gradient를 계산하는 것은 별 의미가 없을 것이므로 current policy이 \(s_i\)에서 할 법한 action의 gradient를 계산하는 것이 낫습니다.
\[\log \pi_{\theta} ( \color{red}{ a_i^{\pi} } \vert s_i)\]당연히 이것도 sampling은 아닙니다 policy network에 \(s_i\)를 넣기만 해도 \(a_i^{\pi}\)를 알 수 있으니까요. 마찬가지로 gradient estimator에도 \(\hat{A}^{\pi} (s_i, \color{red}{ a_i^{\pi} } )\)를 씁니다.
\[\nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_i \nabla_{\theta} \log \pi_{\theta} ( \color{red}{ a_i^{\pi} } \vert s_i) \hat{A}^{\pi} (s_i, \color{red}{ a_i^{\pi} } )\]그런데 우리가 Critic을 Q로 하기로 했기 때문에 A를 구하기가 좀 번거로울 것 같습니다.
그래서 실제로는 Q를 쓴다고 하는데,
이래도 잘못된건 없죠.
애초에 action이 얼마나 좋았나?를 measure하는 quantity는 Q,V,A 중 아무거나 써도 되니까요.
그런데 이렇게 하면 baseline이 빠짐으로써 variance가 조금 커질 수 있으나,
앞서 쓴 trick처럼 \(s_i\)에 대해 action을 몇개 sampling해 봄으로써 (그 값을 아마 평균을 내서) variance를 쉽게 낮출 수 있다고 합니다.
이거는 trajectory sampling에 비하면 cost가 덜 드니까 괜찮다고 하는데, 생각해보면 trajectory sampling은 simulator (environment)와 interaction을 해야 하는데 반해, 지금은 policy network에 state만 넣어서 sampling 하면 되기 때문입니다.
이제 algorithm loop는 아래와 같이 수정됐습니다. 4번의 A=Q-V가 빠졌고, 3번 value target 구하는 부분이랑 5번 actor의 gradient를 계산하는 부분이 개선됐습니다.
 Slide. 24.
Slide. 24.
하지만 여전히 문제가 있으니 바로 \(s_i\)가 current policy로 부터 sampling 된 것이 아니라는 겁니다. 그니까 일어날 일이 없을 수도 있는 state에 대해서 학습하는게 맞는가? Sergey는 어차피 바꿀수도 없는 거 받아들이라고 합니다. 직관적으로는 optimal policy가 sample할 수 있는 trajectory distribution보다 실제로는 더 넓은 (broader) distribution을 갖게 되는데, 뭐 extra work을 하는것이나 그렇게 나쁠건 없다는 마인드 같습니다.
마지막으로 implementation detail 설명해주는데, 첫째로 Q function을 학습하는 더 좋은 방법들이 있는데, 이는 lecture 7,8에서 다룰 것이니 그때 보고, 둘째로는 4번의 gradient를 구하는 방법에 아까 짧게 말씀드린 Soft Actor-Critic (SAC)에서 쓰인 reparameterization trick을 쓰면 더 간단하고 좋다는 얘기를 합니다.
 Slide. 25.
Slide. 25.
SAC가 더 좋은거니까 궁금하면 좀 읽어보라고 하는 것 같습니다. (보통 reparameterization trick은 sampling 행위가 미분이 불가능 (non-differentiable)한데 이를 mean값에 noise vector를 더하는 식으로 수정해서 미분 가능하게 해주는 방법이므로 비슷한 얘기일 것 같은데 궁금하시면 paper를…)
Improved Actor-Critic
Critics as State-dependent Baselines (Let's think bout bias of estimator)
마지막 subsection의 key question은 바로 unbiased하면서도 variance는 낮은 algorithm을 만드는 방법은 없을까? 입니다.
 Slide. 27.
Slide. 27.
위 slide에는 그동안 알아봤던 Actor-Critic과 Vanilla PG가 있습니다.
Critic을 도입함으로써의 장점은 어떤 time step에서의 gradient of log probability를 계산하는 것에 한번 끝까지 가보는 것이 아니라 expectation을 통해 가능한 정확하게 측정한 값을 곱해주기 때문에 variance가 훨씬 낮다는 거였죠.
하지만 단점으로는 더이상 이 algorithm이 unbiased 하지 않다는 겁니다.
반대로 일반적인 VPG는 Critic 없이 Objective가 전개되기 때문에 variance가 높기 때문에 샘플이 더 많이 필요하거나 learning rate가 작아야 하는 단점이 있는 반면에 bias는 없다고 합니다.
왜 그럴까요?
잘 생각해봅시다. 어떤 추정치 (estimator)의 bias가 있느냐는 expectation을 취했을때 이 값이 실제 값 (True Value)을 나타내냐? 아니냐?를 의미합니다. Vanilla PG는 어떤 state에서 수행한 action을 평가하는 quantity로 실제 environment가 준 reward만을 (합해서) 사용합니다. 여기에 어떤 상수를 빼더라도 이는 expectation을 취하면 실제 값이 나올것입니다. 다만 Vanilla PG는 그 값의 분포가 너무 넓은, 즉 high variance할 뿐입니다.
Actor-Critic은 반면에 Value Function이 return해주는 값을 사용합니다.
이 network가 학습하는 것 자체가 실제 reward이므로 학습이 잘 되면 bias는 0에 수렴할 수도 있지만 제대로 학습이 되지 않는다면 gradient는 unbias가 아닌 것이 되는겁니다.
Sergey는 bias가 생겼기 때문에 더이상 policy가 제대로 된 곳으로 수렴하지 않을 수도 있다고 합니다.
그러면 Actor-Critic은 나쁜걸까요?
아닙니다.
말씀드린 것 처럼 학습만 잘되면 bias는 줄어드므로 조금의 손해를 감수하더라도 variance가 매우 낮은 estimator는 쓸 법 합니다.
그런데 variance는 조금 높지만 unbiasd estimator는 쓸 수 없는걸까요??
답은 가능하다고 합니다.
그것은 critic을 baseline으로 만 쓰는 방법을 쓰는겁니다.
원래의 PG는 sum of total reward에다가 baseline으로 trajectory들의 평균을 쓰는 constant baseline를 썼는데, 뒤의 constatnt baseline만 갈아끼우는 거죠.
하지만 critic이 state에만 의존하는 function이므로 이것을 baseline으로 쓰는것은 여전히 gradient estimator를 unbias 하게 만든다고 합니다.
 Fig.
Fig.
이 수식이 slide 21의 가장 아래에 적혀 있습니다.
\[\nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \sum_{t=1}^T \nabla_{\theta} \log \pi_{\theta} (a_{i,t} \vert s_{i,t}) ( (\sum_{t'=t}^T \gamma^{t'-t} r (s_{i,t'}, a_{i,t'} ) ) - \color{red}{ \hat{V_{\phi}^{\pi}} (s_{i,t})} )\](실제로 unbias 한가? 이 증명을 원하시면 이전 chatper인 lecture 5 처럼 하면 된다고 하네요)
Control Variates: State-dependent Baselines
그렇다면 bias 를 감수하고서라도 baseline 으로 state, action에 모두 dependent한 function을 써도 될까요? 답은 yes라고 합니다. 이런 걸 Control Variates라고 하는데 일이 좀 더 일이 복잡해진다고 합니다.
 Slide. 28.
Slide. 28.
다시 Q,V,A를 써봅시다.
\[\begin{aligned} & Q^{\pi}(s_t,a_t) = \sum_{t'=t}^T \mathbb{E}_{\pi_{\theta}} [r(s_{t'},a_{t'}) \vert s_t,a_t] & \scriptstyle{\text{ total reward from taking } a_t \text{ in } s_t} \\ & V^{\pi} (s_t) = \mathbb{E}_{a_t \sim \pi_{\theta}(a_t \vert s_t)} [Q^{\pi}(s_t,a_t)] & \scriptstyle{\text{ total reward from } s_t} \\ & A^{\pi} (s_t,a_t) = Q^{\pi}(s_t,a_t) - V^{\pi}(s_t) & \scriptstyle{\text{ how much better } a_t \text{ is}} \\ \end{aligned}\]State에서 행한 action에 대한 평가, A는 Q-V였죠? 우리는 unbias 하면서 lower variance를 갖는 것으로 아래의 수식을 쓰기로 했었습니다.
\[A^{\pi} (s_t,a_t) = \sum_{t'=t}^{\infty} \gamma^{t'-t} r(s_{t'},a_{t'}) - V_{\phi}^{\pi}(s_t)\]여기서 V함수 대신 Q함수를 approximate해서 사용하면 아래와 같이 됩니다.
\[A^{\pi} (s_t,a_t) = \sum_{t'=t}^{\infty} \gamma^{t'-t} r(s_{t'},a_{t'}) - \color{red}{Q_{\phi}^{\pi}(s_t,a_t)}\]잘 생각을 해 봅시다. V가 아닌 Q를 쓴다는 것은 \(s_t\)에서 action \(a_t\) 를 한 번 하고, 그 다음 \(s_{t+1}\)의 V를 쓰는것과 동치였습니다. 그러니까 sampling이 한 번 들어가는 것이라고 할 수 있는데, 이럴 경우 critic이 (이제 s,a를 input으로 scalar를 뱉는 Q가 critic임) 정확해질 수록 미래에 선택할 행동 (future behavior)들이 랜덤이 점점 아니게 되므로, 거의 같은 action을 하게되므로 Critic이 잘 학습됐다면 이를 expectation 취했을 때 0을 return 한다고 합니다.
하지만 불행하게도, 이렇게 정의한 Advantage Estimator를 VPG에 끼워넣게 되면 gradient가 더이상 정확해지지 않게 되는데 왜냐하면 error term이 추가되기 때문이라고 합니다.
\[\nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \sum_{t=1}^T \nabla_{\theta} \log \pi_{\theta} (a_{i,t} \vert s_{i,t}) ( \hat{Q}_{i,t} - Q_{\phi}^{\pi} (s_{i,t},a_{i,t}) ) \\ + \frac{1}{N} \sum_{i=1}^N \sum_{t=1}^T \nabla_{\theta} \mathbb{E}_{a \sim \pi_{\theta} (a_t \vert s_{i,t} )} [ Q_{\phi}^{\pi} (s_{i,t},a_t) ]\]위의 수식은 state dependent baseline을 쓸 때도 유효한데, state dependent baseline을 쓰면 두 번째 항이 0이 되므로 우리가 아는 수식인 첫 번째 항만 남는다고 합니다. 하지만 Q를 baseline으로 쓸 경우 두 번째 항이 더이상 0가 아니게 된다고 하는데, 두 번째 항은 현재 정책 하의 Value에 대한 expectation의 gradient라고 합니다.
첫 번째 항은 학습을 할수록 수렴할테니 0에 가까워질 것이지만 두 번째항은 꽤 커보일 수 있다고 합니다. 그래서 이게 좋냐?하면 몇몇 case들은 그렇다고 하는데요, 그 case들은 expectation을 꽤 정확하게 구해낼 수 있는 경우라고 합니다. 만약 action space가 discrete하다면 (‘up,down,left,right’ 이런 식), Q값은 정확히 sum하면 구할 수 있는 값이고, continuous하더라도 그 state에서 action을 여러 번 sampling하는 것은 simulator와 상호작용 하는 일이 아니기 때문에 꽤 할만 하다고 합니다. 아니면 아예 Q fucntion의 distribution이 expectation이 계산 가능한 form이라면 (예를 들어 gaussian) 됩니다.
첫 번째 항은 \(\hat{Q} - Q\)로 굉장히 작아질것이고, 두 번째 term도 굉장히 variance가 작은 어떤 값이 되므로 우리는 action, space 두 가지에 dependent한 baseline을 쓰고도 variance는 줄이면서 bias도 없는 Objective를 쓸 수 있다는 겁니다. (더 궁금하신 분들은 Q-Prop: Sample-Efficient Policy Gradient with An Off-Policy Critic을 읽어보라고 하시네요)
N-Step Returns
이제 정말 마지막인데, 마지막으로 알아볼 것은 variance가 작은 Actor-Critic 같은 형태이지만 bias도 최대한 낮추려면 어떻게 해야 할까? 에 대한 솔루션 입니다.
Eligibility Traces와 N-Step Returns이라는 keyword를 slide에서 볼 수 있습니다.
먼저 elgibility의 경우 ‘적임, 책임’ 이라는 사전적 의미를 가지는데, 다시 말해 어떤 state가 얼마나 기여했는지에 대한 책임을 묻고 더 큰 가중치를 주겠다 이런 느낌인 것 같은데 왜 갑자기 이 얘기를 하는지 모르겠습니다. 이 slide에서는 제가 듣기로는 n-step return에 대한 이야기 밖에 안하거든요. RL의 유명한 concept중 하나인 것 같긴 하나 나중에 revisit 하겠습니다.
 Slide. 29.
Slide. 29.
먼저 지겹도록 살펴본 Actor-Critic에 사용되는 Advantage Estimator를 다시 아래와 같이 씁니다. 기존 vanilla Actor-Critic은 subscript 에 c를 붙혀주도록 하겠습니다.
\[\hat{A}_{\color{red}{C}}^{\pi} (s_t,a_t) = r(s_t,a_t) + \gamma \hat{V}_{\phi}^{\pi} (s_{t+1}) - \hat{V}_{\phi}^{\pi} (s_{t})\]여러번 말하지만, Actor-Critic은 Variance가 적은 대신에 Value가 조금이라도 틀리면 완전히 틀어져버릴 수 있는 bias가 존재합니다. Monte Carlo (MC) 방법을 사용하고 Baseline은 Value Function으로 사용한 경우는 Variance는 크지만 bias가 없습니다. MC sampling을 해서 action을 평가하는 방법은 subsciprt로 MC를 붙혀주겠습니다.
\[\hat{A}_{\color{red}{MC}}^{\pi} (s_t,a_t) = \sum_{t=t'}^{\infty} \gamma^{t'-t} r(s_{t'},a_{t'}) - \hat{V}_{\phi}^{\pi} (s_{t})\]이 두가지를 다시 쓴 이유는 바로 bias/variance tradeoff를 컨트롤하기 위해서 두 가지를 적절히 섞을 수 있는 방법은 없을까?에 대해서 생각해보기 위해서 입니다.
Key idea는 “시간이 흐를수록 variance가 커질 가능성이 높으니 가까운 시점, 예를들어 \(t\) 부터 \(t+5\) 까지는 \(A_{MC}\)로, 그 뒤부터는 variance가 크니 \(A_C\)“로 하자는 겁니다.
왜 이게 먹힐지 생각해봅시다. 첫 번째로 variance 에 대해서 생각해보길 시간이 많이 흐르지 않은 경우에는 variance가 크지 않기 때문입니다. Sergey의 비유를 예로 들어보자면 제가 이 글을 쓰는 시점의 5분 뒤에 분당에 거주할 확률은 매우 크죠? 1개월, 3개월 후는 어떨까요? 아마 직장을 관두지 않는 이상 같은 곳에 거주할테니 여전히 확률이 높겠지만 2년, 3년 … n년 뒤에는 제가 미국에 가있을 확률도 존재합니다. 그 정도로 시간이 흐를수록 제가 위치할 곳의 확률 분포에 대한 분산이 커지는 거죠.
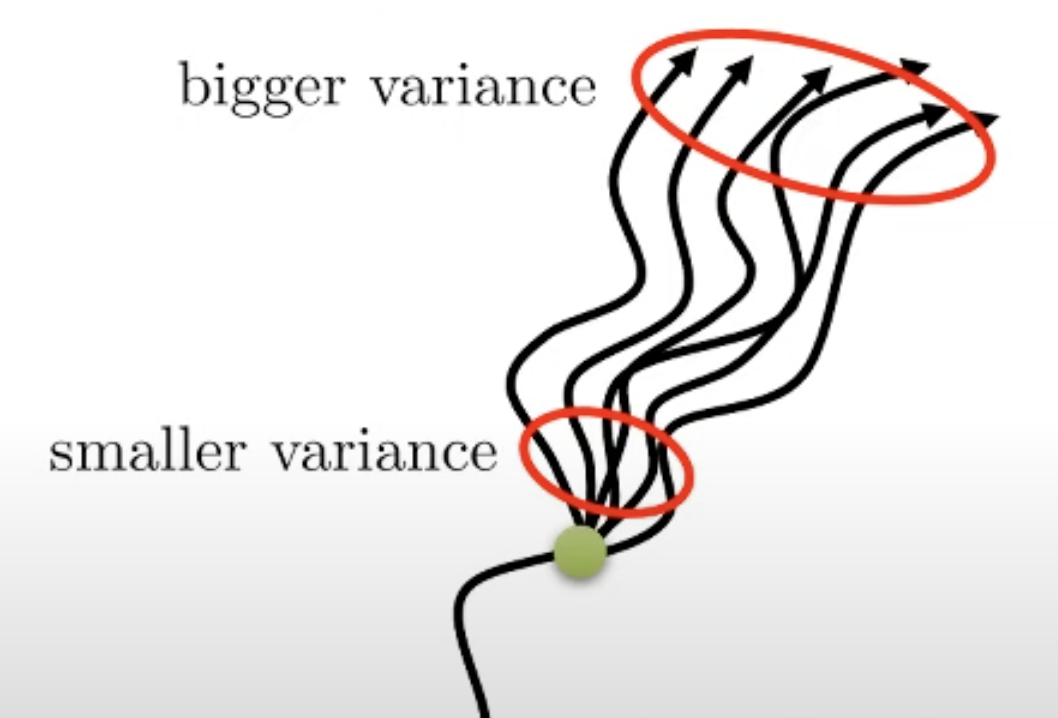 Fig. t가 증가할수록 커지는 variance. 경우의 수가 많아 진다.
Fig. t가 증가할수록 커지는 variance. 경우의 수가 많아 진다.
두 번째로 bias에 대한 생각해 볼 건데, 우리가 t시점의 \(s_t\)에서 \(a_t\)를 한 경우 이 action에 대한 reward의 합은 t로부터 멀어질수록 discount factor가 계속 곱해집니다. 그러니까 해당 t시점에서 몇 step이 지나면 이미 \(\gamma=0.99\)같은 것이 여러 번 곱해져서 값이 작아지기 때문에 Value Function으로부터 생기는 bias가 그렇게 큰 문제가 되지 않는다고 합니다.
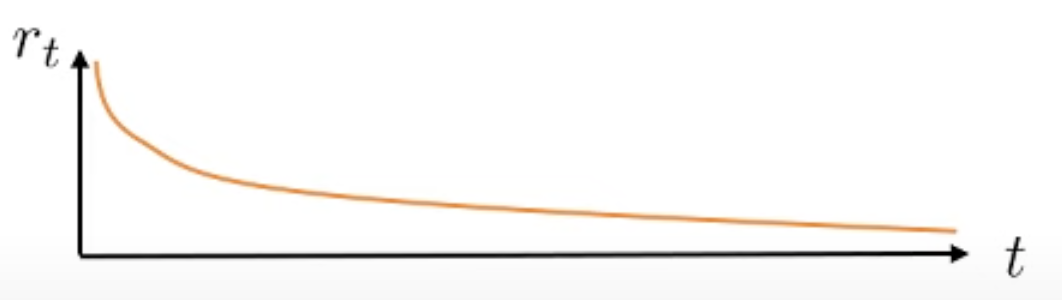 Fig. t가 증가할수록 discount factor가 거듭 곱해져 reward값은 작아짐. Actor의 gradient estimator 입장에선 별 차이 없어지는 것.
Fig. t가 증가할수록 discount factor가 거듭 곱해져 reward값은 작아짐. Actor의 gradient estimator 입장에선 별 차이 없어지는 것.
그렇게 제안된 N-Step Returns Advantage Estimator는 아래와 같이 쓸 수 있습니다.
이는 \(A_{MC}\)를 \(\infty\)까지 해보는 것이 아니라 \(n\)번만 해본다는 점에 주의 해 주시고,
여기서 \(n \sim \infty\)는 \(A_{MC}\)와 동치가 됩니다.
일반적으로 n은 1보다 큰 값으로 정하는게 좋고 일반적으로 n이 커질수록 마지막 term인 Value Function앞에 곱해지는 \(\gamma^n\) 덕분에 마지막 term값이 작아지면서 bias가 작아지지만 variance가 커지고 n이 작을 때는 그 반대가 됩니다.
첫 번째 텀이 variance를 컨트롤하고, 마지막 term이 bias를 컨트롤 하는 셈이 되는거죠.
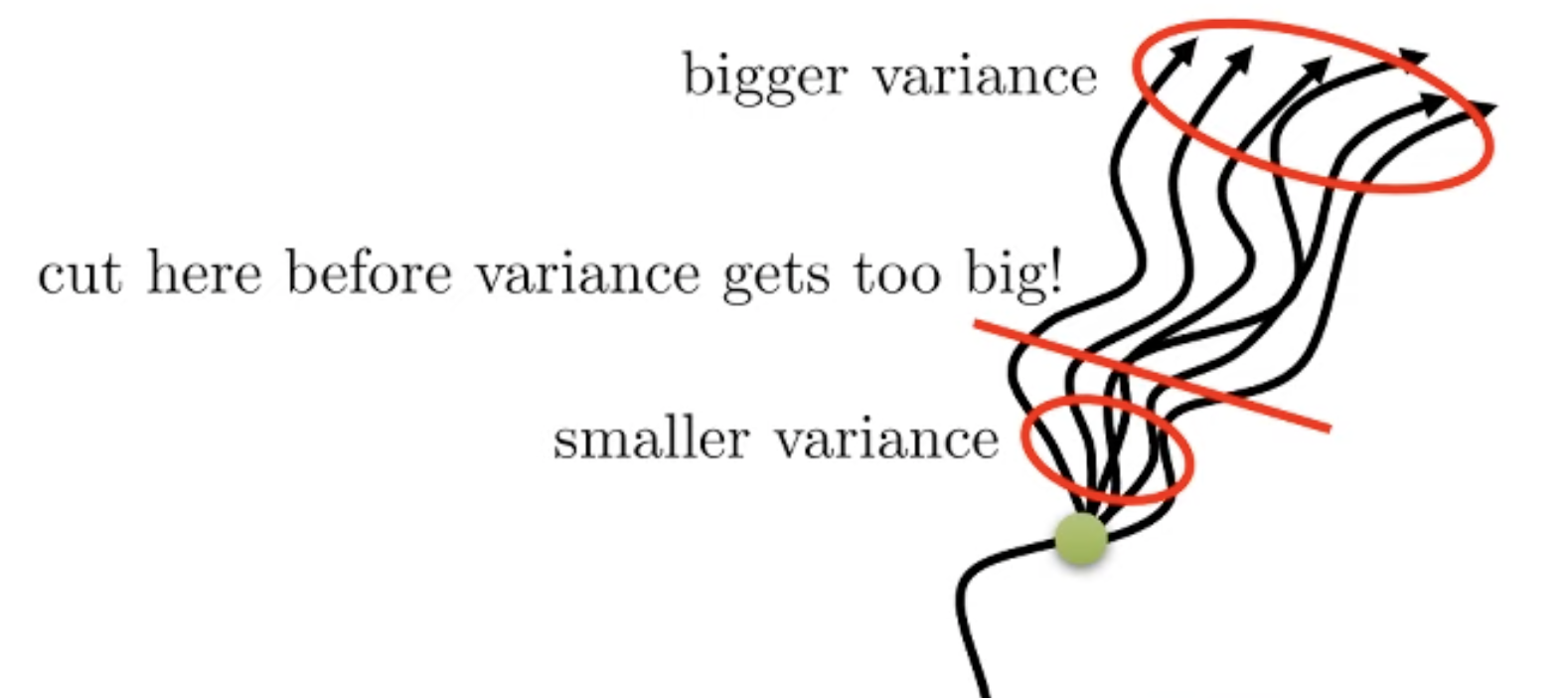 Fig. n이 커질수록, 늦게 자를수록 variance는 커짐.
Fig. n이 커질수록, 늦게 자를수록 variance는 커짐.
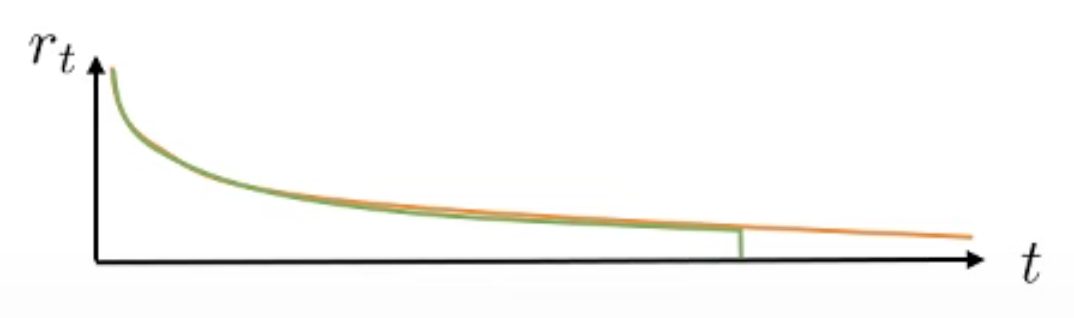 Fig. n이 커질수록, 늦게 자를수록 bias는 작아짐.
Fig. n이 커질수록, 늦게 자를수록 bias는 작아짐.
Generalize Advantage Estimation (GAE)
마지막으로 소개드릴 것은 Generalize Advantage Estimation (GAE)입니다. (저자진에는 역시나 Sergey Levine이 있고, OpenAI의 co-founder이자 research scientist인 John Schulman과 Sergey와 같이 Berkeley에서 RL 연구를 리딩하는 Peter Abbeel이 있습니다.)
 Slide. 30.
Slide. 30.
이 N-step method를 일반화 하면 바로 2015년에 제안된 방법론으로, n-Step Return이 좋은 algorithm이긴 하나 어떻게 n을 설정할지가 까다롭기 때문에 GAE는 이를 해결하고 싶었고, \(n=1 \sim \infty\) 까지 n-step return을 weighted-sum 한 형태를 띄게 됩니다.
\[\begin{aligned} & \hat{A}_{n}^{\pi} (s_t,a_t) = \sum_{t=t'}^{t+n} \gamma^{t'-t} r(s_{t'},a_{t'}) - \hat{V}_{\phi}^{\pi} (s_{t}) + \gamma^n \hat{V}_{\phi}^{\pi} (s_{t+n}) & \\ & \hat{A}_{\color{red}{GAE}}^{\pi} (s_t,a_t) = \sum_{n=1}^{\infty} w_n \hat{A}_{n}^{\pi} (s_t,a_t) & \\ \end{aligned}\]최종적인 수식은 아래와 같이 되는데, 이를 유도하기 위해서는 \(w_n \approx \lambda^{n-1}\)로 두고 paper의 유도를 따라가야 함으로 따로 paper를 보시길 추천드립니다. 이렇게 하면 어쨌든 n-step return의 n을 1부터 … 다 한 효과를 누릴 수 있다고 합니다. 이럴 경우 우리가 이제 n을 고를 필요는 없고 \(\lambda\)만 잘 정해주면 된다고 합니다.
\[\begin{aligned} & \hat{A}_{\color{red}{GAE}}^{\pi} (s_t,a_t) = \sum_{n=1}^{\infty} (\gamma \color{green}{\lambda})^{t'-t} \color{blue}{\delta_{t'}} & \\ & \text{where } \color{blue}{\delta_{t'}} = r(s_{t'},a_{t'}) + \gamma \hat{V}_{\phi}^{\pi}(s_{t'+1}) - \hat{V}_{\phi}^{\pi} (s_t) & \\ \end{aligned}\]살짝 종합해보자면 우리가 Actor, Critic 학습을 할 때 각 parameter \(\pi, \phi\)는 당연히 초기화를 잘 해줘야 하겠고, 나머지로 골라야할 hyperparameter는
- 1.rollout 횟수 (batch size): 얼마나 많은 rollout을 한번에 할지?
- 2.learning rate
- 3.discount factor, \(\gamma\)
- 4.lambda, \(\lambda\)
가 되겠습니다. 하지만 만약 \(\lambda\)가 1이면 어떻게 될까요? 사실 이렇게 해도 학습이 잘 된다고 합니다. 왜냐하면 앞에 \(\gamma\)가 그 역할을 대신 해 줄 것이기 때문입니다. 그래서 우리가 앞서 discount factor, \(\gamma\)가 infinite horizon case를 해결할 뿐 아니라 variance를 줄여주기도 한다고 했는데, 그것의 해석이 될 수 있는것이죠.
Review, Examples, and Additional Readings
이제 이론적인 내용은 다 끝났고 마지막 subsection에서는 리뷰와 demo video를 동반한 예시를 보여줍니다.
 Slide. 31.
Slide. 31.
Examples
이하 Slide. 33.~Slide. 35.는 비디오 데모가 포함되어 있기 때문에 강의를 참조하시길 추천드리며, 마지막 슬라이드는 추천할만한 Actor-Critic Based 논문들 이므로 시간이 되시는 분들은 따로 논문을 찾아보시길 바랍니다.
 Slide. 33.
Slide. 33.
 Slide. 34.
Slide. 34.
 Slide. 35.
Slide. 35.
Outro
이제 아래의 Deep RL Taxonomy에서 Policy Gradient based Algorithm은 거의 커버를 한 것 같습니다.
 Source from Reinforcement Learning Coach from Intel Lab
Source from Reinforcement Learning Coach from Intel Lab
 Source from OpenAI Spinning Up form OpenAI
Source from OpenAI Spinning Up form OpenAI
Lecture 7부터는 value based method에 대해 알아보게 될 것입니다.
Additional) Things to Think about
Sparse Reward Problem
추가로 sparse reward problem에서는 각 state들이 어떤 value를 배우게 되는지?에 대해서 얘기해 봅시다.
먼저 아래와 같이 Actor, Critic을 위한 separating network 2개가 존재하고, episode가 T=10에서 끝난다고 칩시다. rollout을 한 번 했을 때 아래와 같이 \((s_1,a_1, s_2,a_2, \cdots, s_9,a_9, s_T,a_T)\) 같은 trajectory가 만들어 질겁니다.
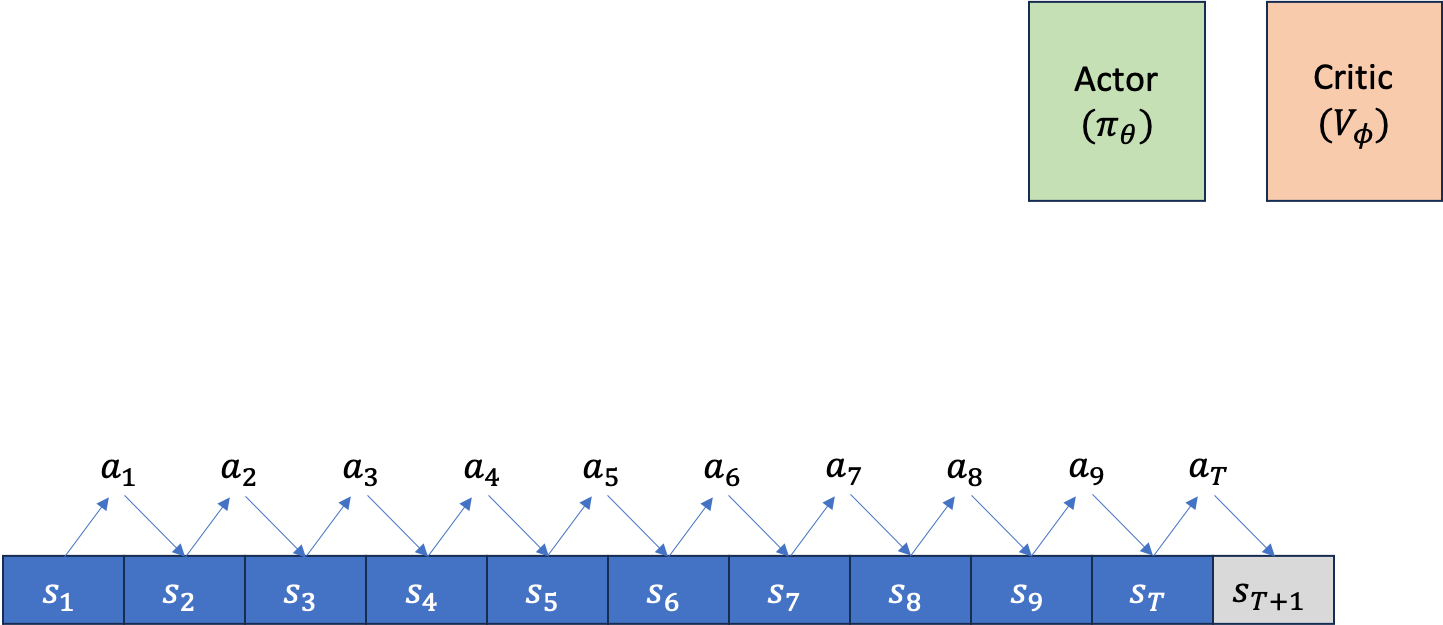 Fig.
Fig.
만약 이 task가 episode가 끝나는 시점에만 reward를 알 수 있는 sparse reward problem이 아니라 dense reward problem이라면, 주어진 trajectory tuple에 reward가 포함될 겁니다\((s_1,a_1,\color{red}{r_1} s_2,a_2,\color{red}{r_2} \cdots, s_9,a_9,\color{red}{r_9} s_T,a_T,\color{red}{r_T})\).
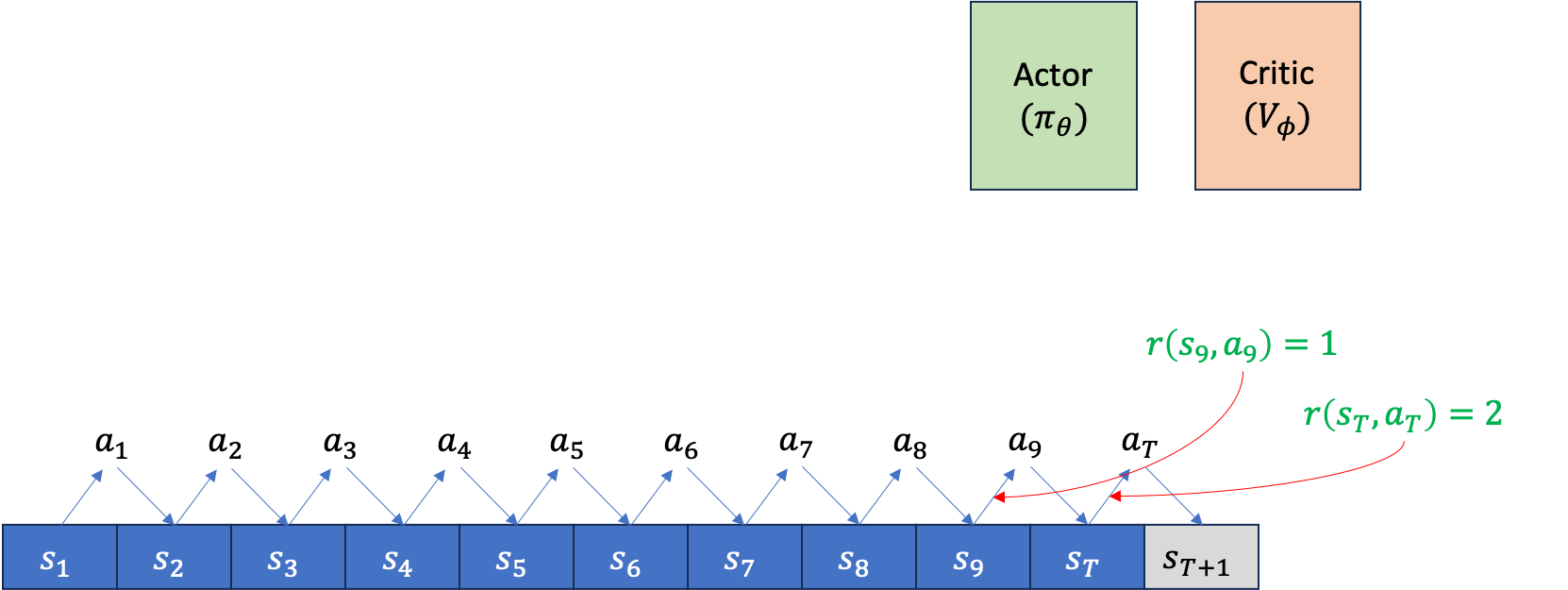 Fig.
Fig.
이제 주어진 각 시점의 state, \(s_t\)에서 action, \(a_t\)를 했을 때 그 action의 reward을 평가해야 gradient를 추정할 수 있겠죠? Advantage Function, A 값을 구합니다.
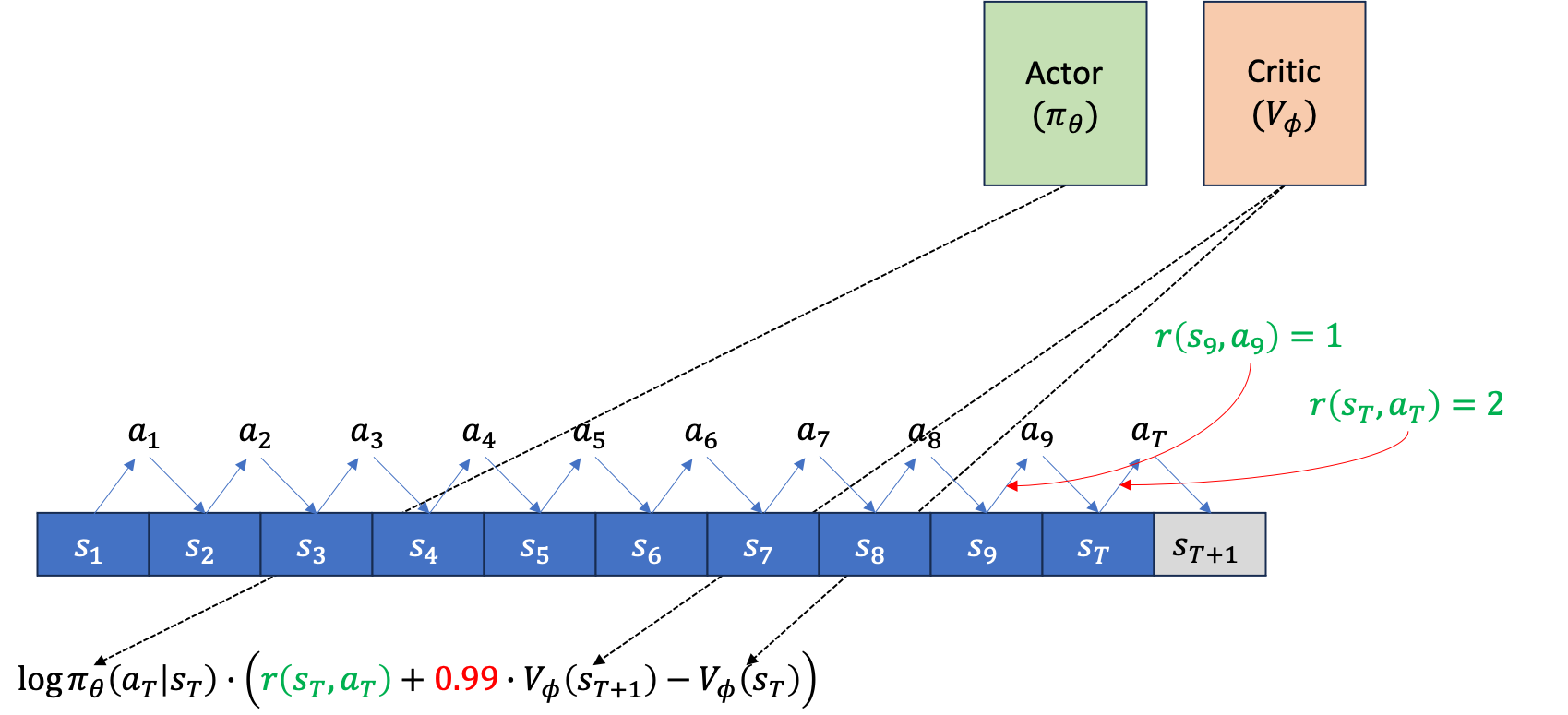 Fig.
Fig.
만약 single sample estimate 으로 평가했으면 \(\sum r - V(s_t)\) 같은 형태여야겠지만, 지금은 bootstrap estimator를 사용했으며, discount factor, \(\gamma\)도 적용됐습니다. 이제 이를 모든 action에 대해서 평가합니다.
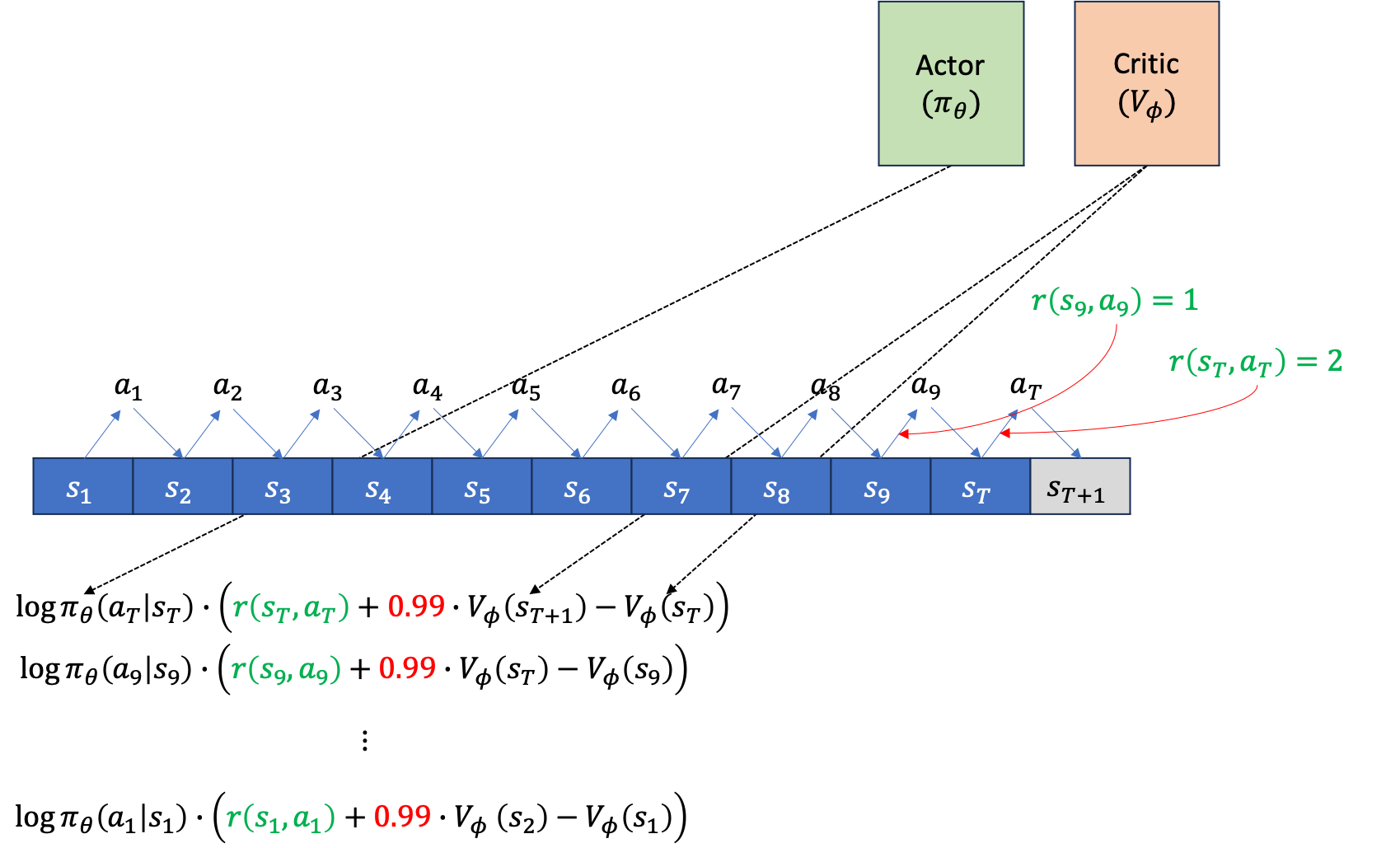 Fig.
Fig.
이제 위의 gradient log prob 에 A를 곱한 gradient를 backpropagation 하면 Actor는 update됩니다. 그 다음에 우리가 얻은 quantity들로 Critic도 업데이트 해야겠죠? Bootstrap 방식을 썼으니 Critic network의 target은 아래와 같습니다.
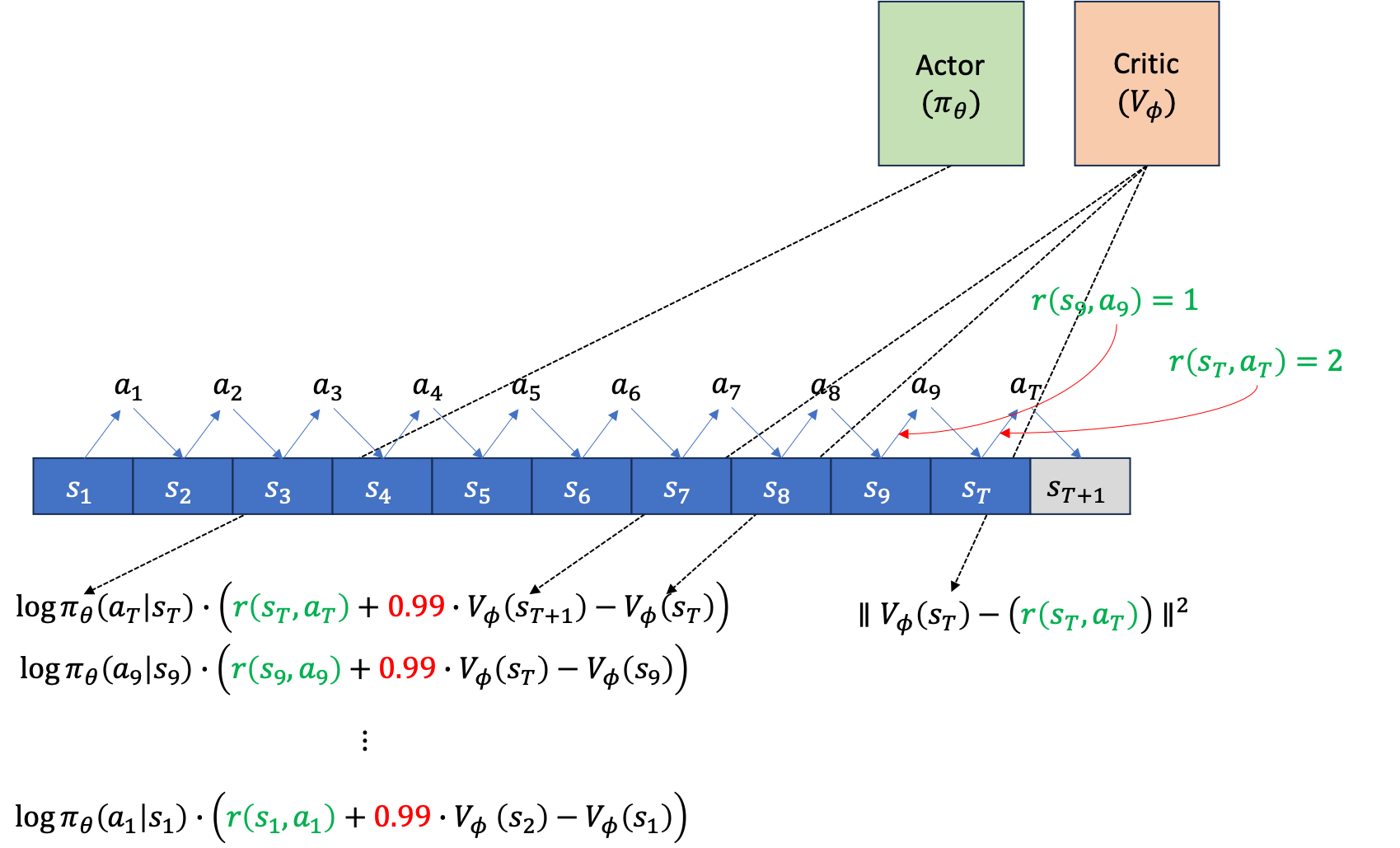 Fig.
Fig.
여기서 마지막 terminal state, T에서의 target은 \(V(s_{t+1})\)이 없기 때문에 \(r(s_T,a_T)\)만 존재합니다. 이를 마찬가지로 \(s_1\)에서 \(s_T\)까지 진행해 줍니다.
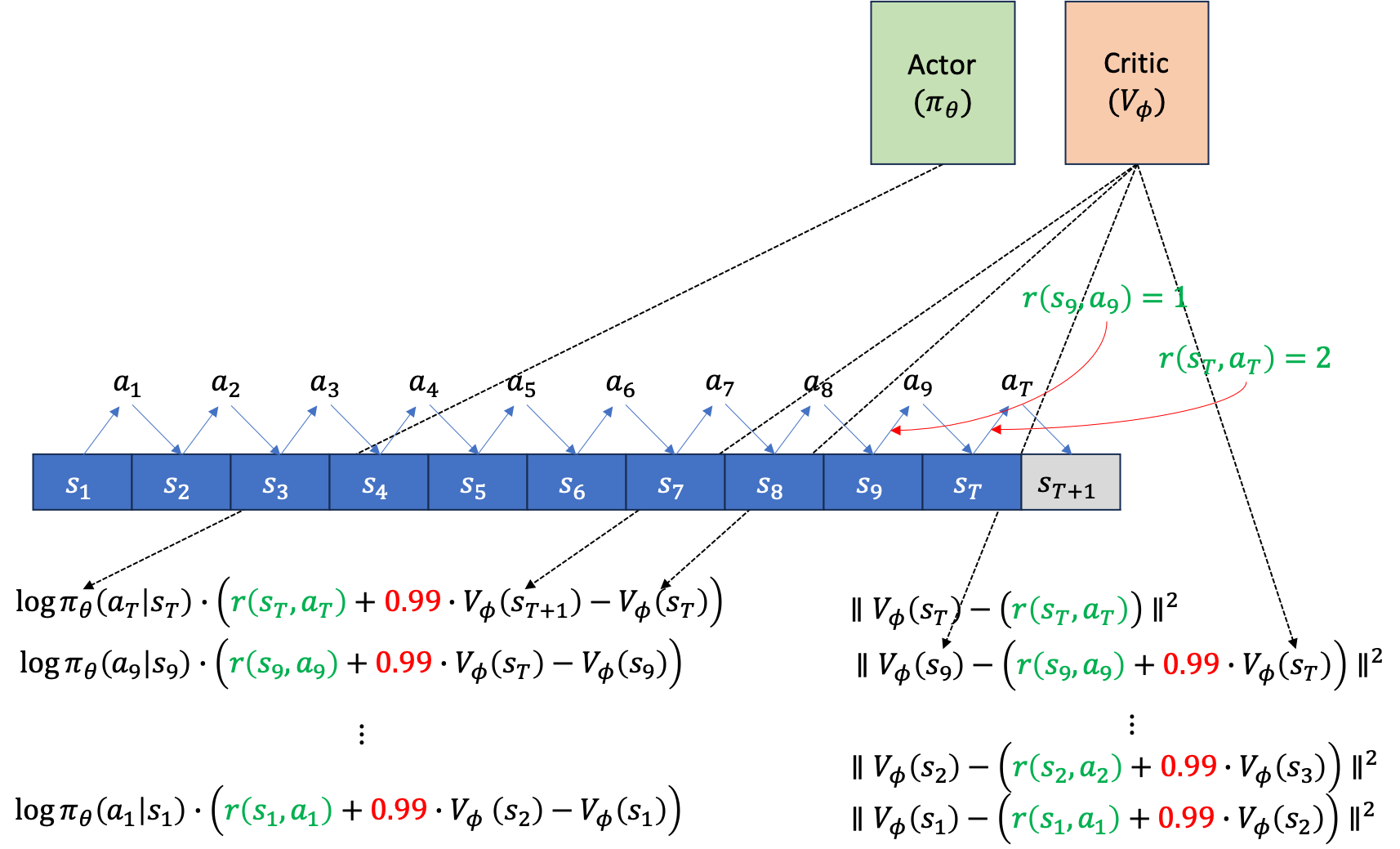 Fig.
Fig.
하지만 만약 우리가 sparse reward problem과 마주했다면 어떻게 될까요?
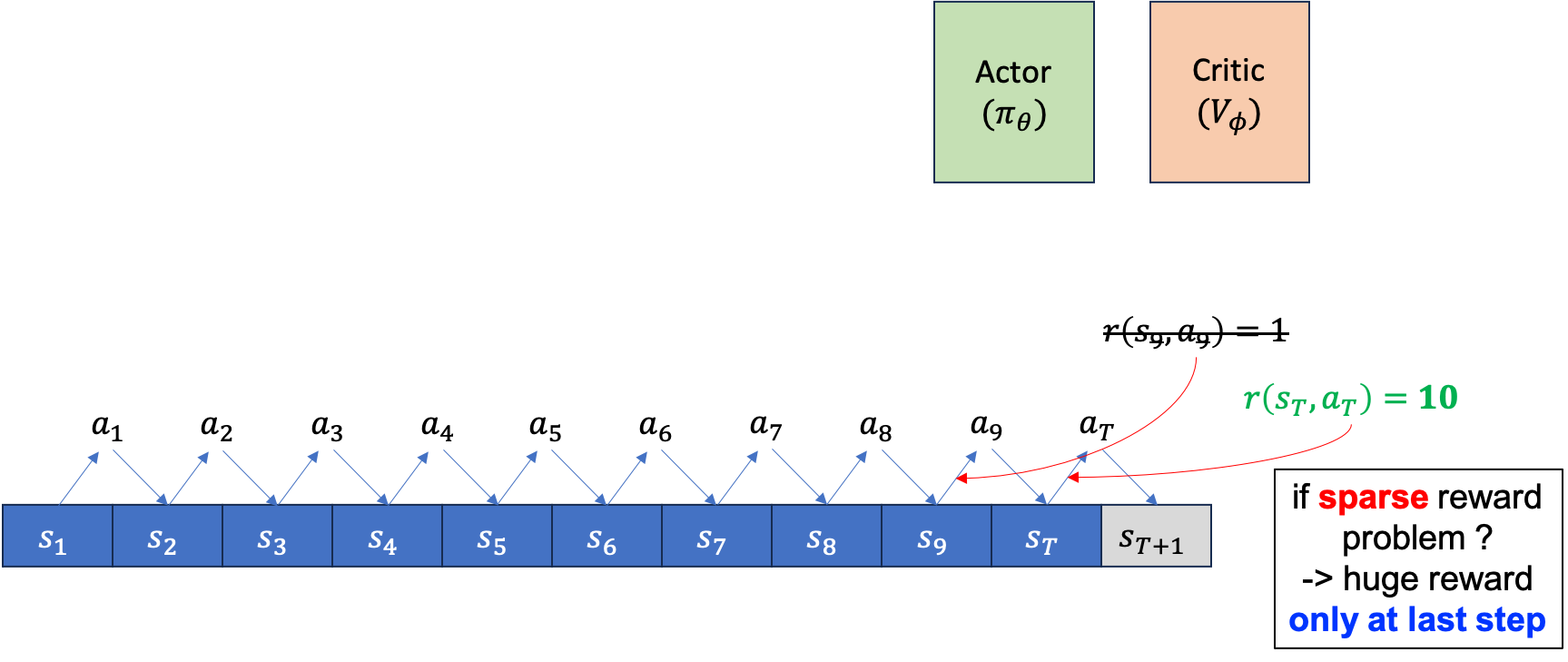 Fig.
Fig.
sparse reward problem은 매 \(s_t,a_t\)마다 \(\color{red}{r_t}\)라는 reward를 주지 않습니다. 다만 episode가 끝나면, 예를 들어 바둑같은 경우 이기면 1점 지면 0점을 받는 식이죠. 그럴 경우 Actor에 대한 gradient estimator에도 각 state별 reward는 없는 셈이 되며, Critic의 target또한 마찬가지가 됩니다.
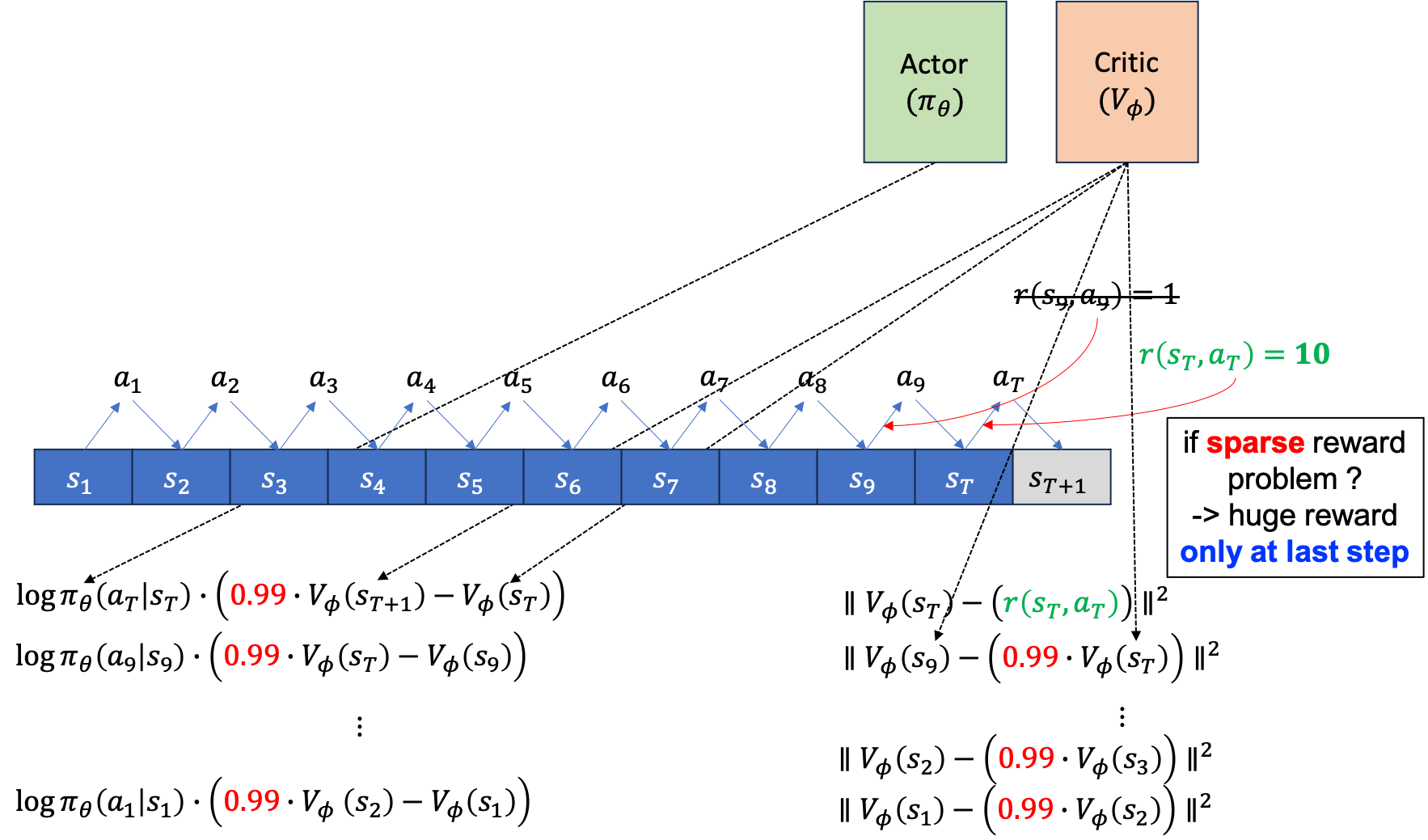 Fig.
Fig.
여기서 Critic의 Target을 보시면 episode의 끝에서 만약 10점을 받았다면 state들의 value값이 \(10*0.99\), \(10*0.99^2\), \(10*0.99^3\) … 같은 값을 예측하게 될겁니다.
그러면 최종 episode의 결과가 양수일 경우 각 state들의 value 값은 잘 학습됐다는 가정하에 모두 양수이며 initial state로 갈 수록 지수적으로 감소하는 형태가 될 것입니다.
점점 reward가 전파 (propagation)되는 것 이죠.
그리고 당연하게도 action에 곱해지는 advantage function 또한 항상 양수가 될것이므로 모든 action의 확률이 증가하는 방향으로 학습될 겁니다.
즉 바둑을 둔다고 쳤으면 바둑의 승패가 결정날 때 까지 200수가 걸렸다고 할 때 Agent가 둔 200수의 확률이 모두 좋아지는 겁니다.
그러면 어떤 trajectory의 모든 state들에 대해서 Critic의 output value가 그리는 curve는 거의 continuous해야 할까요? 그리고 return이 좋다는 이유로 모든 action이 좋게 평가되는게 맞을까요? 실제로 처음부터 학습을 하는 Agent가 둔 수 중에서는 200수 중에서 어떤 수들은 바둑의 신이 보기에는 안좋은 수들이었을 겁니다. 왜 이 수들은 penalty를 받지 않는걸까요?
앞서 dense reward problem에서는 이런 식의 reward propagation이 있었지만 environment가 t시점의 s,a을 했을 때 준 reward가 더해지기 때문에 별로 문제가 되지 않아보입니다만 sparse reward problem에서는 문제가 되는 것 처럼 보입니다. 하지만 이런 경우에도 결국에는 좋지않은 수는 나쁜 reward를 받아 확률이 깎이고 좋은 수는 좋은 확률이 높아질 겁니다. 그 이유는 학습 시 trajectory를 sampling하는 rollout을 수 없이 많이 하기 때문입니다. 각 trajectory들 중에서 어떤 trajectory는 안좋은 episode return을 받아서 그 동안 두었던 수들의 확률을 낮춰야 할텐데, 서로 다른 trajectory들끼리 이를 보강/간섭? 하기 때문에 우리가 원하는 대로 어떤 state 에서 어떤 action이 좋았던 상황이 더 많으면 확률이 오르는 것이고, 어떤 trajectory에서는 그 수가 좋다고 평가받았지만 대부분의 경우 안좋다고 평가받았으면 그 수는 결국에는 확률이 낮아지기 때문이죠.
이는 일반적인 Supervised Learning (SL)과도 맥락이 비슷합니다. 우리가 단어들이 주어졌을 때 그 다음 단어를 맞추는 언어 모델링 (Language Modeling; LM)이나 음성 인식 (Automatic Speech Recognition; ASR)도 같은 맥락에서 다른 단어들을 말하는 경우를 많이 보고 일반화 하기 때문에 잘 동작하는 것이죠.
Reference
- Lectures
- CS 285 at UC Berkeley : Deep Reinforcement Learning
- Deep RL Bootcamp (Berkeley 2017)
- CS 224R Deep Reinforcement Learning from Chelsea Finn
- [CMU 10-703 Deep Reinforcement Learning from Katerina Fragkiadaki]
- Papers