(CS285) Lecture 5 - Policy Gradients
02 Nov 2023이 글은 UC Berkeley 의 교수, Sergey Levine 의 심층 강화 학습 (Deep Reinforcement Learning) 강의인 CS285를 듣고 작성한 글 입니다.
Lecture 5의 강의 영상과 자료는 아래에서 확인하실 수 있습니다.
- Fall 2020 ver.
< 목차 >
- Recap
- Direct Policy Differentiation
- Reducing Variance
- Off-Policy Policy Gradients
- Implementing Policy Gradients
- Advanced Policy Gradients
- Outro
- Reference
이번 lecture에서 배울 내용은 정책 경사 (Policy Gradient; PG) algorithm 입니다.
Policy gradient based method들은 RL의 objective function을 정책의 parameter \(\theta\)에 대해서 직접 (directly) 미분해 policy 그 자체를 직접적으로 update하여 개선하는 method 입니다.
 Slide. 1.
Slide. 1.
Recap
(lecture 4의 recap은 간단히 넘어가도록 하겠습니다.)
 Slide. 2.
Slide. 2.
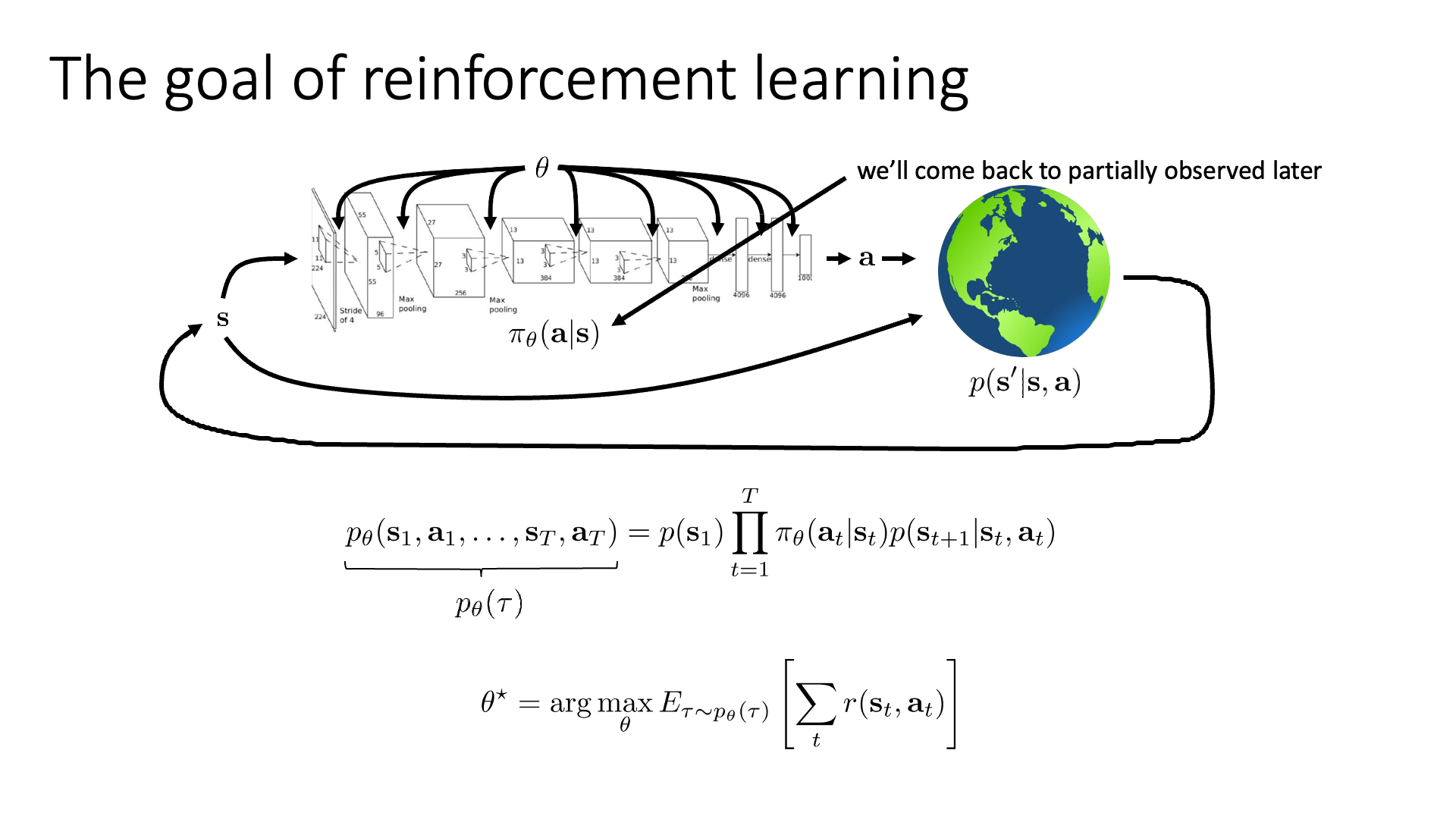
Policy는 어떤 state에서 어떤 action을 해야하는지? action distribution을 return해주는, state (input)과 action (output)을 연결해주는 mapping function입니다. Deep RL 에서는 Neural Network (NN)으로 policy를 modeling하므로 NN의 parameter가 곧 policy의 parameter가 됩니다. Action의 distribution 형태 는 Deep Learning (DL)의 Supervised Learning (SL)처럼 continuous (regression)하면 Gaussian distribution, discrete (classification) 하면 Categorical distribution으로 modeling하면 됩니다.
Figure에서 알 수 있듯 policy를 통해 timestep t에서의 state, \(s_t\)의 action \(a_t\)를 probabilistic distribution으로 부터 산출해 내면 \((s_t,a_t)\)를 given으로 다음 state, \(s_{t+1}\)로 이동하게 되는데, 이는 그 다음 state가 어떻게 될지?를 의미하는 transition operator (or transition dynamics), \(p(s_{t+1} \vert s_t, a_t)\)에 의해 결정됩니다. 이 tensor \(T\)는 우리가 처음부터 알고 있을 수도 아닐 수도 있는데, 우리가 어떤 simulation 환경을 만들어서 미로 찾기 같은걸 할 때 이를 알고 설계할 수도 있으나 대부분의 real-world problem에서는 알려져있지 않습니다. 이를 NN으로 modeling할 수도 있는데, 이런 경우를 Model-based RL이라 한다고 했습니다.
궤적 (Trajectory)이란 한 episode 내의 일련의 state, action들 \((s_1, a_1, s_2, a_2, \cdots, s_T, a_T)\) 의 모음이며, 이 trajectory distribution은 현재 policy에 따라 정해집니다 (당연하게도 trajectory distribution은 어떤 state에서 어떤 action을 할 확률이 몇인지를 알아야 제대로 표현할 수 있는데, 이것이 곧 policy를 의미하기 때문). 그리고 chain rule에 따라서 이 distribution은 initial state distribution, transition probability와 policy의 곱으로 분해 (factorization) 될 수 있었습니다.
한편, Model-based RL과 다르게 transition probability를 모르는 상태에서 sampling을 통해 학습을 진행하는 것을 Model-free RL라고 합니다.
마지막으로 우리가 최종적으로 optimize할 RL Objective는 현재 policy를 따르는 trajectory distribution하에서의 total reward의 기대값이었습니다. 모든 RL algorithm들은 이 objective를 maximize하는, good policy를 찾는 것이 goal입니다.
\[\theta^{\ast} = \arg \max_{\theta} \mathbb{E}_{\tau \sim p_{\theta}(\tau)} [ \sum_t r(s_t,a_t) ]\]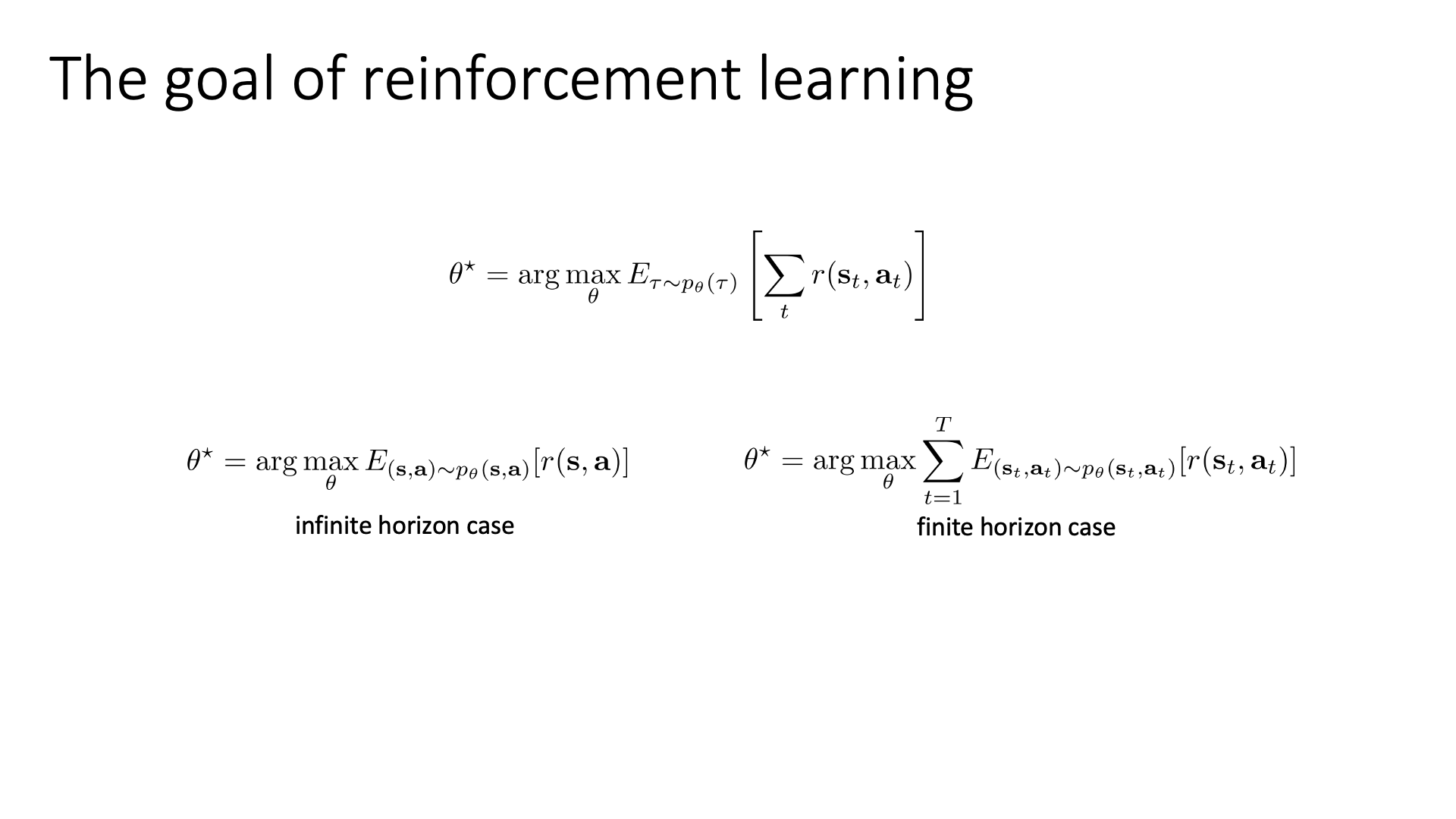 Slide. 3.
Slide. 3.
Slide 3은 RL의 obejective function을 state-action marginal을 사용해서 표현하면 episode의 끝이 없는 infinite horizon case와 끝이 정해진 fintie horizon case 둘 다에 대해서 objective function을 정의할 수 있음을 recap한 것입니다.
Lecture 5부터 lecture 6까지는 lecture 4 말미에 소개해드린 policy based method에 대해서만 detail하게 알아봅니다. Policy based method는 value-based method와 다르게 policy를 parameterize 하는 명시적인 (explicit) NN을 정의합니다. 그 다음 total reward의 expectation을 의미하는 RL objective funcion을 policy parameter에 대해서 직접 미분해 gradient를 구합니다. 그리고 DL에서 많이 쓰는 gradient descent처럼 update하면서 optimal policy를 찾는 method 라고 했습니다.
이제 본격적으로 어떻게 RL objective function을 parameter에 대해 미분해 gradient를 계산하는지 알아봅시다.
Direct Policy Differentiation
앞서 RL의 objective function를 현재 policy를 따르는 trajecotry distribution 하에서 trajectory를 따라 끝까지 episode를 마쳤을 때 얻을 수 있는 return (reward의 합)의 expectation으로 정의했습니다. 이걸 policy에 gradient descent같이 1차 미분하여 optimization step을 1회 하면 policy update가 한 번 이루어집니다.
 Slide. 4.
Slide. 4.
Objective function은 다시 아래와 같습니다.
\[\theta^{\ast} = \arg \max_{\theta} \mathbb{E}_{\tau \sim p_{\theta}(\tau)} [ \sum_t r(s_t,a_t) ]\] \[J(\theta) = \mathbb{E}_{\tau \sim p_{\theta}(\tau)} [ \sum_t r(s_t,a_t) ]\]만약 우리가 “초기 state가 어디에 놓여질까?”를 의미하는 initial state distribution \(p(s_0)\)와 “어떤 상태에서 어떤 행동을 하면 그 다음 상태는 어떻게 될까?”를 의미하는 transition dynamics, \(p(s_{t+1} \vert s_t, a_t)\)를 모른다고 하면 어떻게 \(J(\theta)\)를 계산할 수 있을까요?
Full expectation을 계산하지 않고 근사할 수 있는 방법이 있는데 바로 sampling을 하는 겁니다.
Initial state distribution으로 \(s_0\)를 sampling하고 그 뒤로는 current policy를 직접 run해서 trajectory를 뽑는거죠.
(이는 lecture 4의 orange block에 해당합니다.)
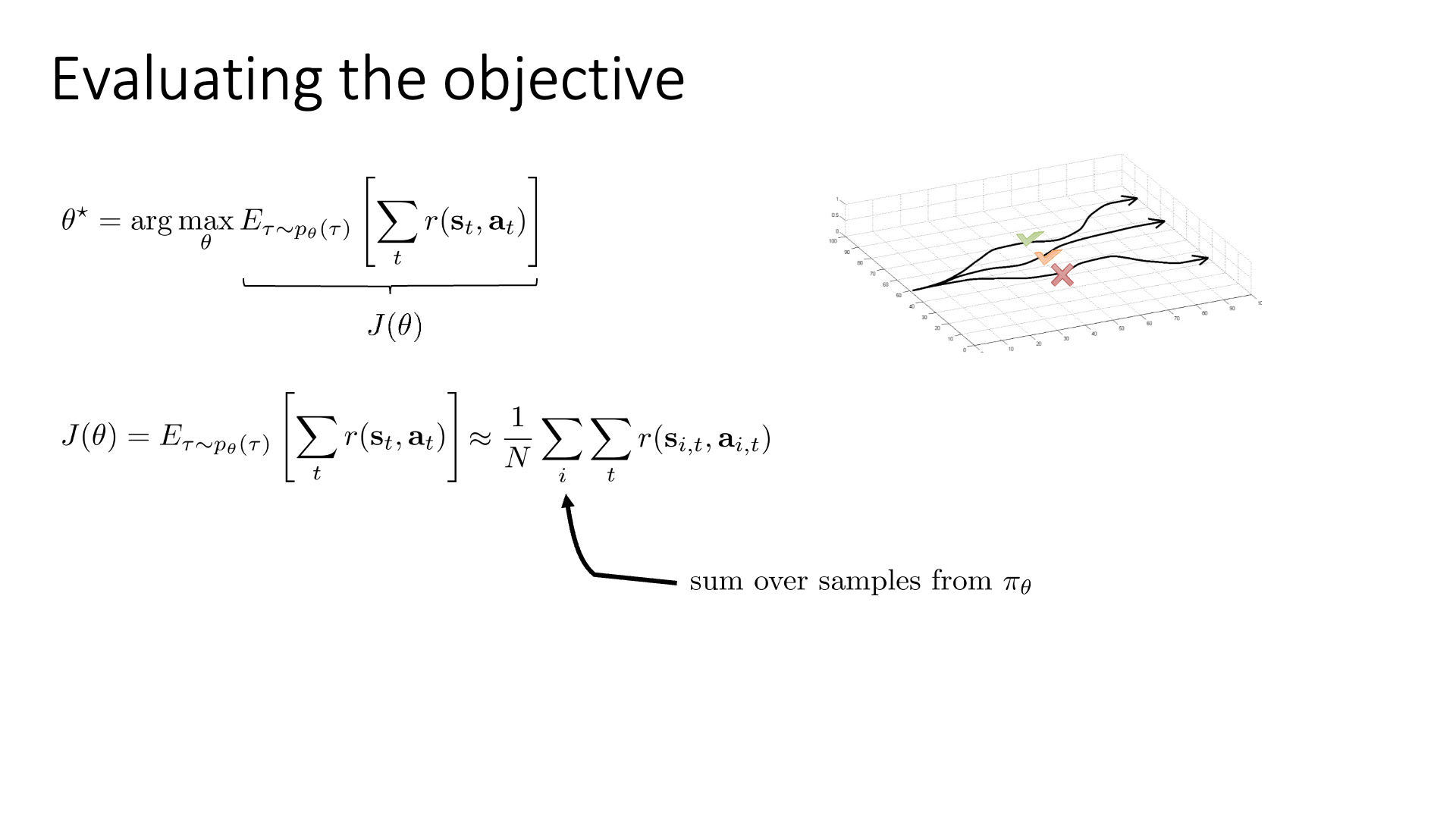
Policy를 굴려서 (roll-out 한다고 함) \(N\)개의 trajectory들을 얻었다고 생각합시다. 이제 각 trajectory들을 samplin하면서 매 \((s_t,a_t)\)마다 \(r(s_t,a_t)\)를 enivronment로 부터 받았을 테니 trajectory가 얼마나 괜찮았는지?를 summation으로 계산할 수 있습니다.
이제 \(N\)개의 return을 평균내면 우리는 \(J(\theta)\)를 근사할 수 있는데, 이는 완벽한 full expectation이 아니고 원래 distribution의 variance가 크기 때문에 값이 많이 튀지만, 여전히 unbiased estimation가 된다고 합니다. Unbiased라는 것은 큰 수의 법칙 (Law of Large Number; LLN)에 따라서 이 N을 무한히 키우면 이 sample들의 expectation이 결국 원래 분포의 mean과 같아진다는 걸 의미합니다.
이제 우리는 이 \(J(\theta)\)를 바탕으로 policy를 improvement하고 싶은 것이니 optimization을 해야 하고, gradient based method를 쓰기 위해서는 \(J(\theta)\)에 대한 1차 미분값, \(\nabla_{\theta} J(\theta)\)을 구해야합니다.
 Slide. 5.
Slide. 5.
우선 original objective fucntion의 expectation은 당연히 integral이나 summation으로 다시 쓸 수 있습니다.
\[J(\theta) = \mathbb{E}_{\tau \sim p_{\theta}(\tau)} [ \color{red}{ \sum_{t=1}^T r(s_t,a_t) } ]\] \[\color{red}{ r(\tau) } = \sum_{t=1}^T r(s_t,a_t)\] \[J(\theta) = \color{blue}{ \mathbb{E}_{\tau \sim p_{\theta}(\tau)} } [ \color{red}{ r(\tau) } ]\] \[J(\theta) = \color{blue}{ \int p_{\theta}(\tau) } r(\tau) \color{blue}{ d\tau }\]이제 policy의 parameter \(\theta\)인 지점에 대해 objective function를 미분합니다. Differential operator, \(\bigtriangledown\)는 선형적이기 때문에 이를 적분식 안으로 넣으면 아래와 같이 표현할 수 있습니다.
\[\color{red}{ \nabla_{\theta} } J(\theta) = \int \color{red}{ \nabla_{\theta} } p_{\theta} (\tau) r(\tau) d\tau\]여기서 아래의 identity를 이용하면 (기억이 안나면 고등학교 수학의 log의 미분에 대해서 찾아보면 됨)
\[p_{\theta}(\tau) \nabla_{\theta} \log p_{\theta} (\tau) = \nabla_{\theta} p_{\theta} (\tau)\]아래의 수식을 얻을 수 있습니다.
\[\nabla_{\theta} J(\theta) = \int \color{red}{ \nabla_{\theta} p_{\theta}(\tau) } r(\tau) d\tau = \int \color{red}{ p_{\theta} (\tau) \nabla_{\theta} \log p_{\theta}(\tau) } r(\tau) d\tau\]마지막으로 다시 expectation으로 rewrie을 하면 결국 \(\nabla_{\theta} J(\theta)\)를 얻을 수 있습니다.
\[\nabla_{\theta} J(\theta) = \int p_{\theta} (\tau) \nabla_{\theta} \log p_{\theta} (\tau) r(\tau) d\tau = \color{blue}{ \mathbb{E}_{\tau \sim p_{\theta}(\tau)} } [ \nabla_{\theta} \log p_{\theta} (\tau) r(\tau) ]\]하지만 아직 끝난 것이 아닙니다. 바로 \(\nabla_{\theta} \log p_{\theta} (\tau)\) term 때문입니다. 왜 이것이 문제일까요?
그 이유는 trajectory distribution에는 transition probability가 포함되어 있는데,
대부분의 real world problem의 경우 이것을 알 수가 없기 때문이죠.
 Slide. 6.
Slide. 6.
이제 transition probability 를 없애봅시다.
\[J(\theta) = \int p_{\theta}(\tau) r(\tau) d\tau\] \[\theta^{\ast} = \arg \max_{\theta} J(\theta)\] \[\nabla_{\theta} J(\theta) = \int p_{\theta} (\tau) \nabla_{\theta} \log p_{\theta} (\tau) r(\tau) d\tau = \mathbb{E}_{\tau \sim p_{\theta}(\tau)} [ \nabla_{\theta} \log p_{\theta} (\tau) r(\tau) ]\]먼저 수식의 우변에 존재하는 trajectory distribution를 lecture 4에서 처럼 factorization 합니다.
\[p_{\theta} (\tau) = p_{\theta}(s_1,a_1,\cdots,s_T,a_T) = p(s_1) \prod_{t=1}^T \pi_{\theta}(a_t \vert s_t) \color{red}{ p(s_{t+1} \vert s_t, a_t ) }\]우리가 관심있는 term은 \(\log p_{\theta}(\tau)\)이므로, 양변에 \(log\)를 취하면 아래의 식을 얻을 수 있습니다.
\[\log p_{\theta} (\tau) = \log p(s_1) \sum_{t=1}^T \log \pi_{\theta}(a_t \vert s_t) + \log p(s_{t+1} \vert s_t, a_t )\]우리가 원하는 것은 \(\nabla_{\theta} log p_{\theta}(\tau)\)이기 때문에 양변을 \(\theta\)에 대해서 미분한다고 생각하면 \(\theta\)와 관련없는 term은 날려도 그만이라는 것을 알 수 있습니다.
\[\nabla_{\theta} \log p_{\theta}(\tau) = \nabla_{\theta} [\log p(s_1) + \sum_{t=1}^T \log \pi_{\theta}(a_t \vert s_t) + \log p(s_{t+1} \vert s_t, a_t )]\]즉 transition probability의 \(\theta\)에 대한 미분은 dont care이기 때문에 무시할 수 있고, 최종적으로 다음과 같은 수식을 얻을 수 있게 됩니다.
\[\nabla_{\theta} J(\theta) = \mathbb{E}_{\tau \sim p_{\theta}(\tau)} [ ( \sum_{t=1}^T \log \pi_{\theta}(a_t \vert s_t) ) \color{red}{ r(\tau) } ]\] \[\nabla_{\theta} J(\theta) = \mathbb{E}_{\tau \sim p_{\theta}(\tau)} [ ( \sum_{t=1}^T \log \pi_{\theta}(a_t \vert s_t) ) \color{red}{ (\sum_{t=1}^T r(s_t,a_t)) } ]\]즉 우리는 transition probability이 주어지지 않았어도 몰라도 (혹은 따로 학습하지 않아도) 되고,
expectation, \(\mathbb{E}\)속의 모든 term들이 알려져 있는상황이기 때문에 reward function를 policy의 parameter, \(\theta\)에 대해서 미분하는 것에 아무런 문제가 없게 됐습니다.
(아 여기에 우리가 아까 말했던 것 처럼 \(\mathbb{E}_{\tau}\)를 sampling으로 대체하면 Slide 7 하단에 나와있는 최종 수식을 얻게 됩니다)
 Slide. 7.
Slide. 7.
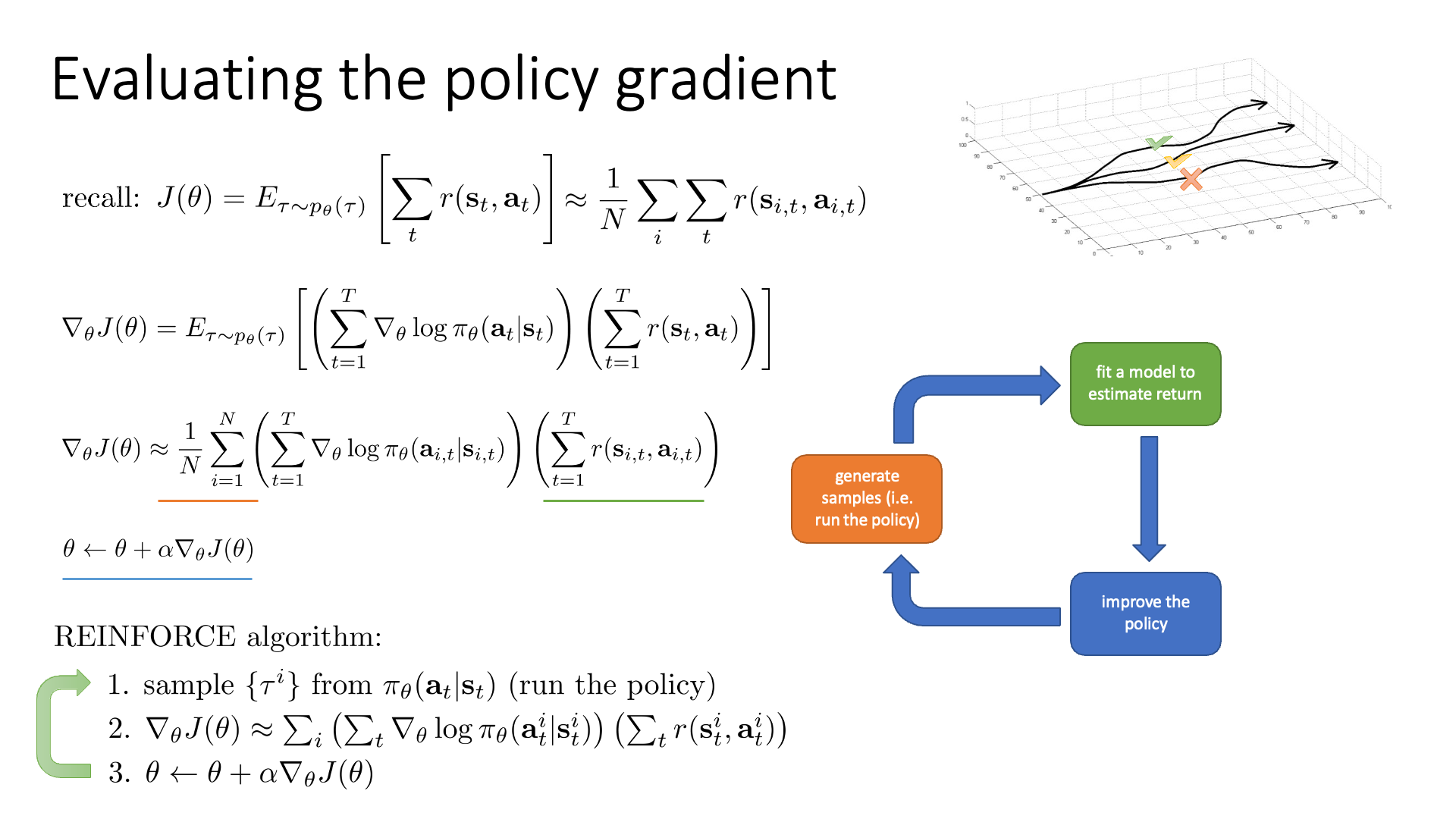
지금까지 유도한 아무런 technique이 없는 policy based method를 (Vanilla) Policy Gradient (VPG)라고 하며,
REINFORCE라고 부릅니다.
REINFORCE algorithm은는1992년에 Williams에 의해 제안되었으며,
slide 7 하단에 나와있는 것 처럼 세가지 step으로 이루어진 loop를 무한히 반복하면 됩니다.
하지만 안타깝게도 지금까지 살펴본 VPG는 real world application에서는 잘 작동하지 않는다고 합니다. 이제 왜 그런지?에 대해서 알아보고 어떻게 개선할 수 있는지 얘기해 봅시다.
Maximum Likelihood vs Policy Gradient
VPG를 개선할 수 있는 방법에 대해 알아보기 전에 Supervised Learning (SL)의 learning algorithm인 Maximum Likelihood Estimation (MLE)와 VPG를 비교해 봅시다. (이미 lecture 2, 4에서 좀 얘기했지만 다시)
 Slide. 9.
Slide. 9.
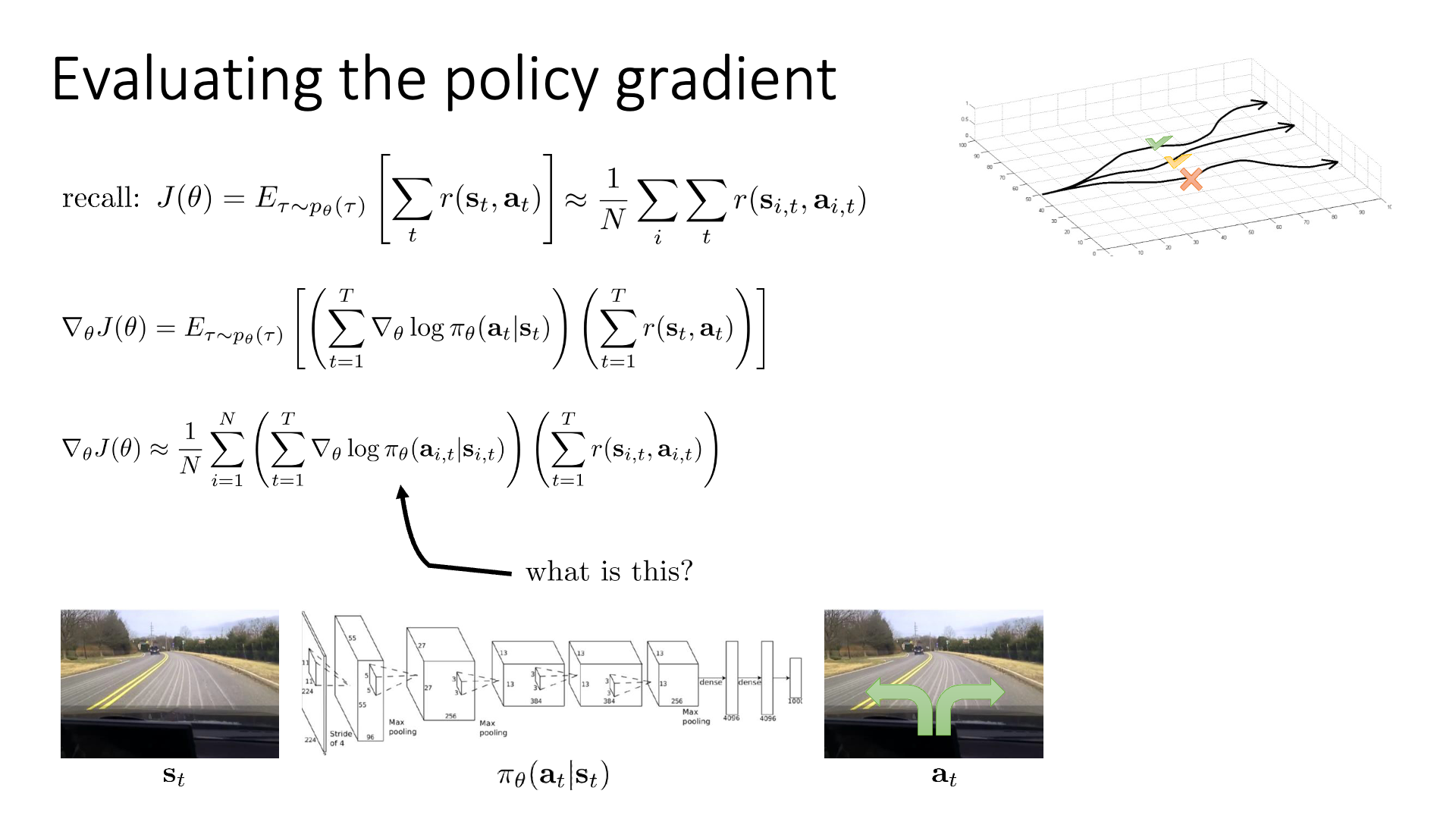
아마 눈치를 채신 분들도 계시겠지만 REINFORCE에서
\[\nabla_{\theta}J(\theta) \approx \sum_{i=1}^N ( \sum_{t=1}^T \nabla_{\theta} \log \pi_{\theta} (a_{i,t} \vert s_{i,t}) ) ( \sum_{t=1}^T r(s_{i,t},a_{i,t}) )\]reward weighting 해주는 부분만 빼면 log likelihood의 미분체만 남게 됩니다.
\[\nabla_{\theta}J(\theta) \approx \sum_{i=1}^N ( \sum_{t=1}^T \nabla_{\theta} \log \pi_{\theta} (a_{i,t} \vert s_{i,t}) ))\](negative log likelihood냐 아니면 log likelihood에 reward weight을 해준 것이냐?의 차이)
 Slide. 10.
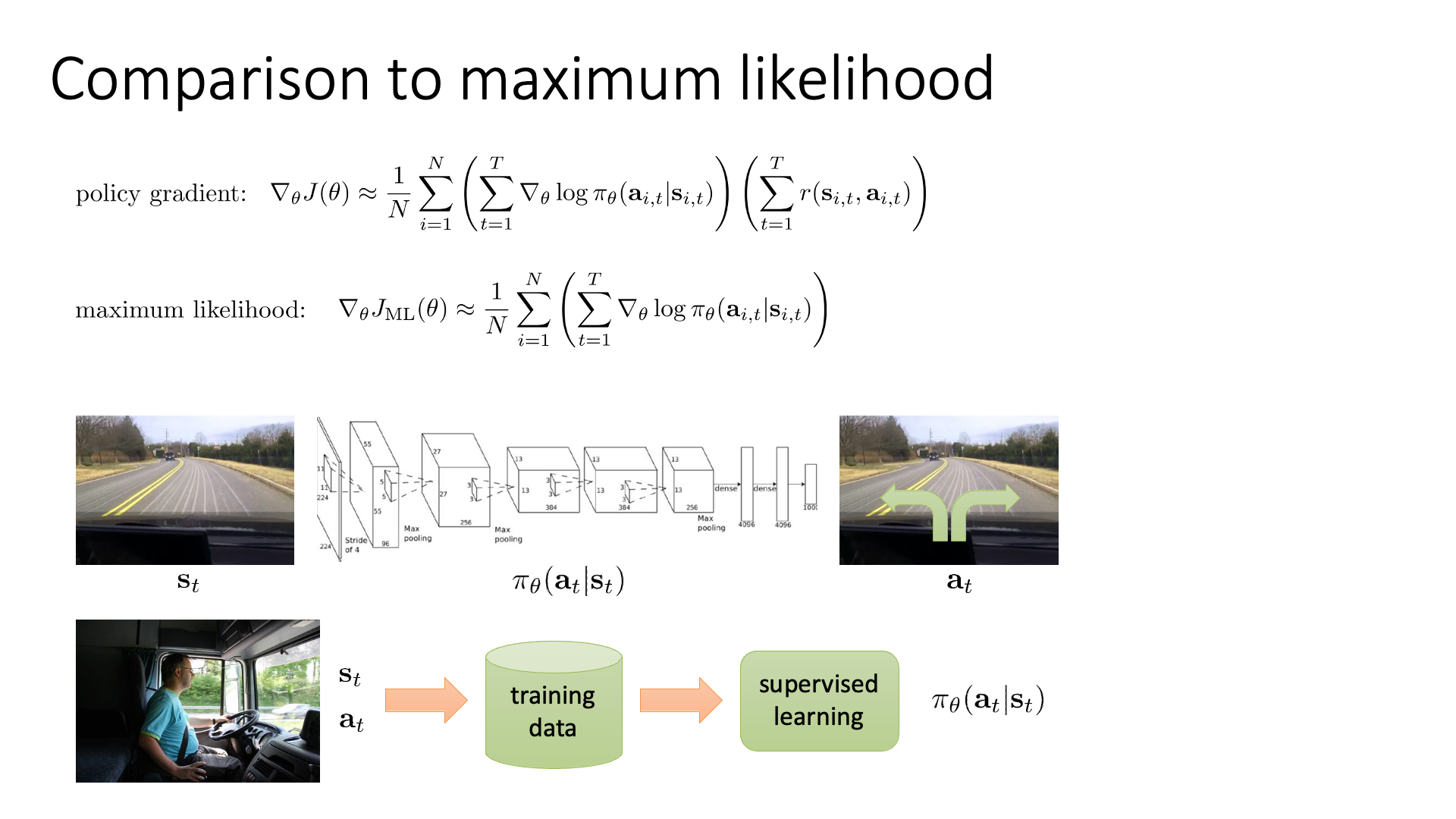
Slide. 10.
SL은 정답 label에 해당하는 action의 확률을 1로 만드는 일을 합니다. 정답의 log probability를 최대화 하는 방향으로 학습하는거죠. SL (혹은 Behaviour Cloning; BC)이 아니기 때문에 매 state마다 어떤 action을 하는 것인지?에 대한 정답 label이 없죠. 대신에 뒤에 \(( \sum_{t=1}^T r(s_{i,t},a_{i,t}) )\)가 붙어있죠. 이는 trajectory의 total reward (return)에 따라서 return이 양수이면 그 action들이 모두 좋았던 것으로 간주하고 (정답이라고 치고) 그 action들의 probability를 증가시키고, return이 양수면 probability를 줄이는 식으로 학습한다는 겁니다. 그리고 얼마나 확률을 높히고 줄일지는 return의 scale에 의해서 정해집니다. (MLE의 경우 모든 정답에 해당하는 action에 reward를 항상 1로 주는 것과 같음)
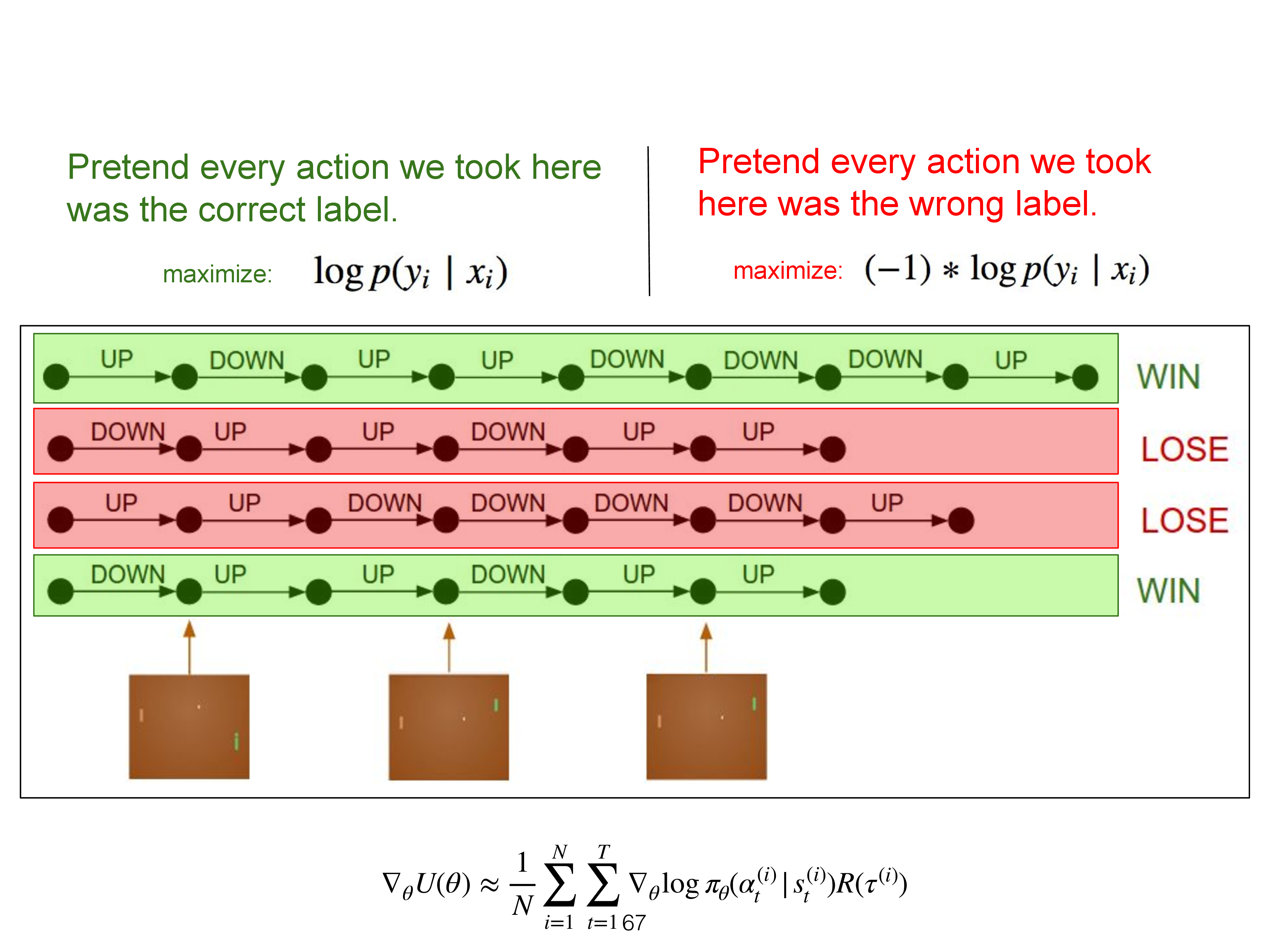 Fig. 확률이 낮아질 수도 있는 RL
Fig. 확률이 낮아질 수도 있는 RL
 Fig. 정답이 없는 RL은 어떤 action의 확률을 높힐것이냐 말것이냐를 정답 label이 아니라 현재 policy와 simulation이 주는 reward를 통해 계산한 Advantage라는 값을 쓴다 (lecture 6에 나옴)
Fig. 정답이 없는 RL은 어떤 action의 확률을 높힐것이냐 말것이냐를 정답 label이 아니라 현재 policy와 simulation이 주는 reward를 통해 계산한 Advantage라는 값을 쓴다 (lecture 6에 나옴)
따라서 REINFOCE를 MLE의 general case 혹은 weighted sum version이라고 얘기할 수도 있겠습니다. 지금의 경우 trajectory의 return에 따라서 그 trajectory를 구성하는 모든 action의 확률이 높아지고 낮아지지만, 경우에 따라서는 trajectory의 return을 따르되 그 중에서도 좋은 action이 있을 수 있으니 이를 고려해서 나쁜 trajectory속에서도 좋은 action을 학습할 수 있게 됩니다.
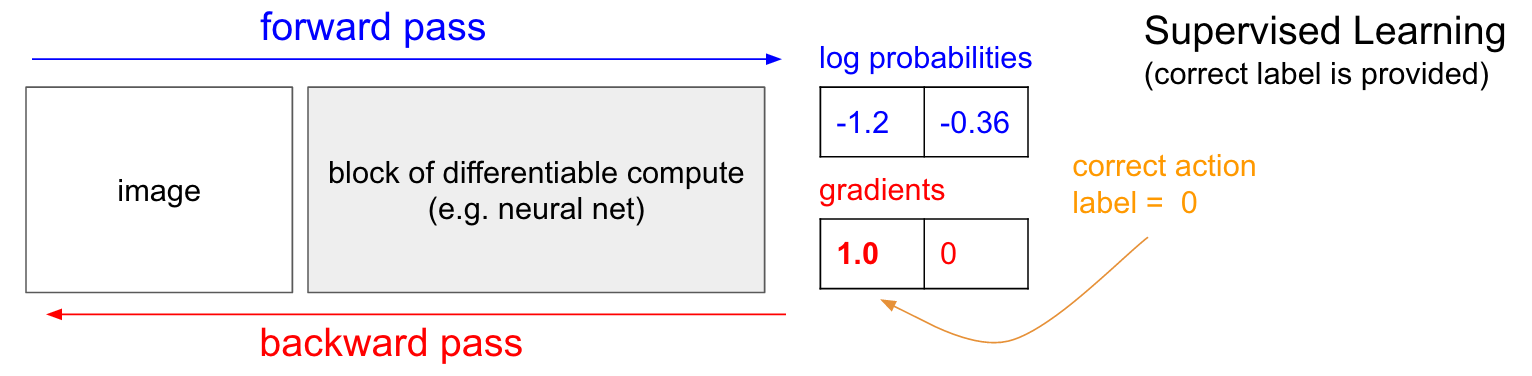 Fig. SL은 언제나 정답인 action에 대해서만 reward를 1을 줌
Fig. SL은 언제나 정답인 action에 대해서만 reward를 1을 줌
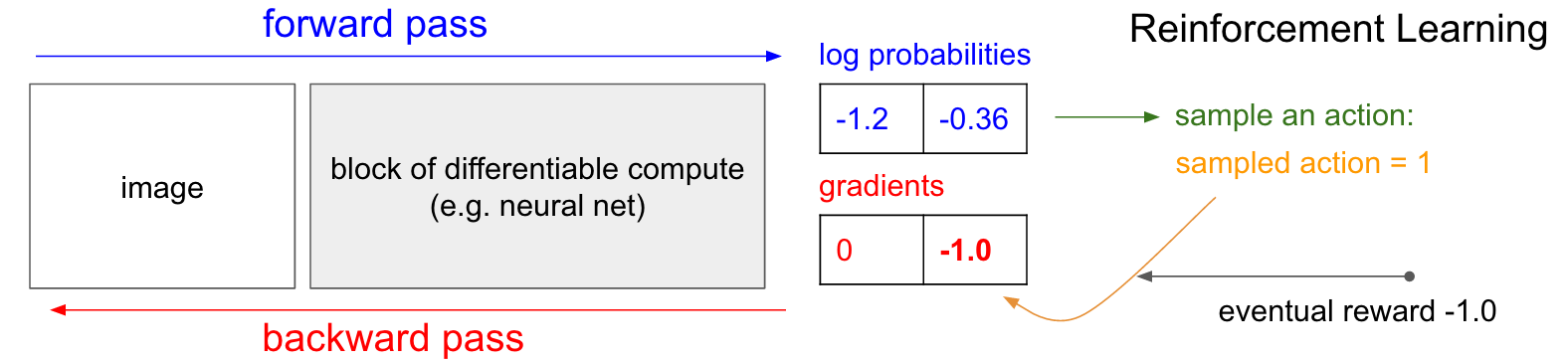 Fig. RL은 내가 한 action에 대해서 일단 이것이 정답인 지도 모르며, +1을 받을 수도, -1을 받을 수도 있음.
Fig. RL은 내가 한 action에 대해서 일단 이것이 정답인 지도 모르며, +1을 받을 수도, -1을 받을 수도 있음.
SL과 달리 RL은 매 iteration step마다 current policy를 따르는 distribution하에서 더 정교해진 trajectory를 계속 뽑고, 그 속에서도 또 평가를 해서 더 좋은 action들을 계속 강화 (reinforce)하는 것으로, 인간을 모사하는것에 그치는 것을 뛰어넘을 수 있다는 점에서 SL과의 차이점이 있다고 할 수 있습니다.
Continuous Space
 Slide. 11.
Slide. 11.
PG의 예시로 humanoid agent가 joint을 control하면서 걷는 task에 대해 언급합니다. 이 problem은 joint을 얼만큼 몇도? 꺾어야 하는 것이기 때문에 action space가 연속적 (continuous)입니다. ML에서는 output distribution을 contiunuous distribution으로 가정하는 경우 gaussian distribution를 씁니다. 이 경우 likelihood를 정의하고 negative log를 씌우면 Mean Squared Error (MSE) Loss 를 얻을 수 있습니다. 아까 CE Loss에 reward term을 weighting 해준 것 처럼 MSE Loss에 reward term을 weighted sum하는걸로 continuous action case의 gradient를 계산해낼 수 있습니다.
 Slide. 12. 앞서 얘기했기 때문에 생략
Slide. 12. 앞서 얘기했기 때문에 생략
Partial Observability
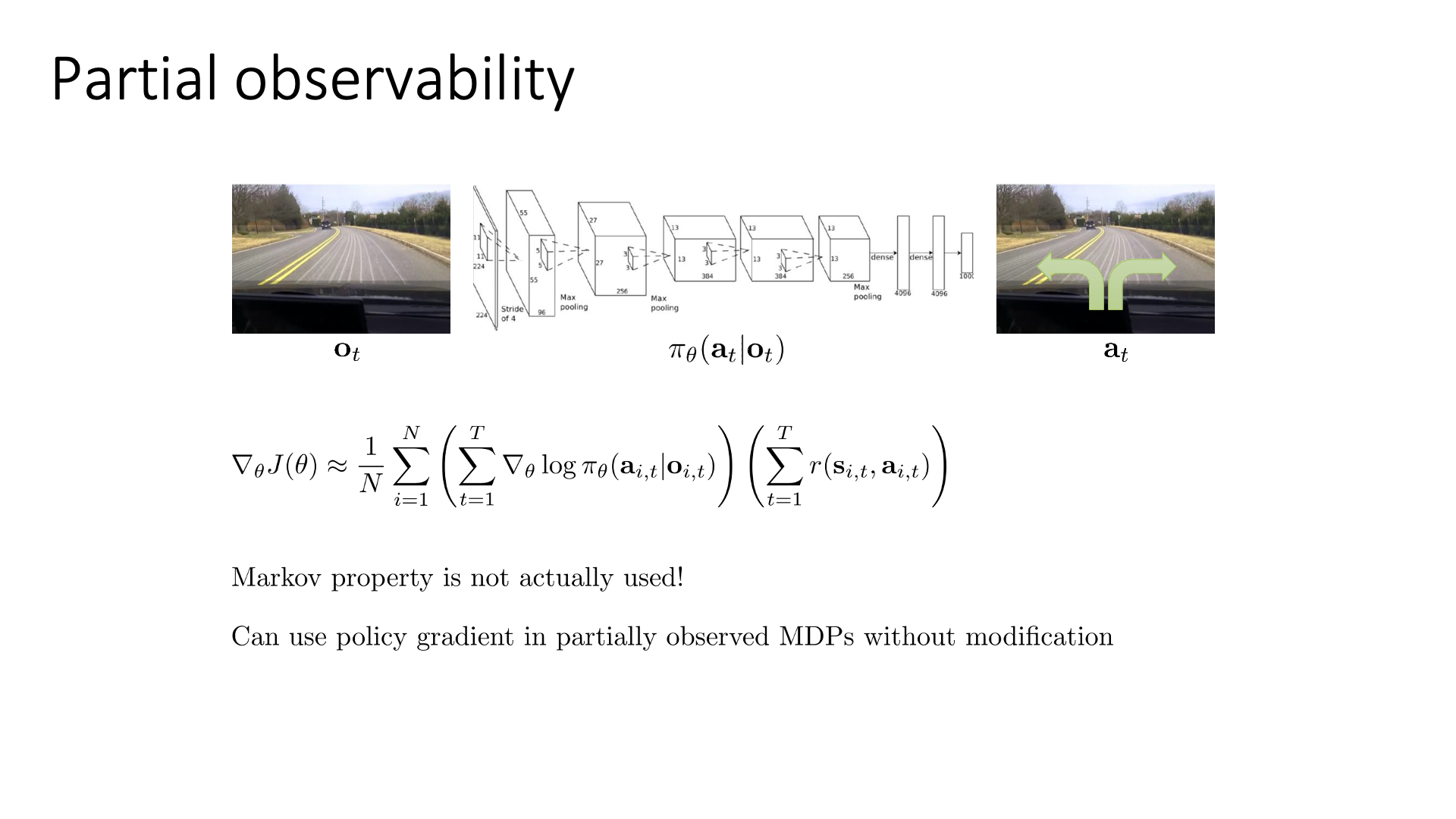
아래 slide는 state가 아니라 observation, \(o\)를 given으로 했을 때의 gradient를 나타냅니다.
 Slide. 13.
Slide. 13.
State와 observation의 차이는 Markov Property를 만족하느냐 아니냐의 차이였는데, 별 문제없이 PG를 POMDP에도 사용할 수 있다고 합니다.
Reducing Variance
Problem of Policy Gradient : Variance
VPG는 굉장히 straightforward하지만 몇 가지 문제점이 존재합니다.
- 1.(Gradient의)
Variance가 크다. - 2.Gradient Descent (Ascent)할 시 얼만큼 가야 하는지?를 의미하는 Step size를 정하기 어렵다.
- 3.Sample Inefficient 하다
(2,3번은 나중에 lecture 9에서 다룰 것인데, TRPO와 PPO)가 이를 해결한 algorithm 입니다)
이는 근본적으로 VPG를 할 때 trajectory distribution하의 return의 expectation을 완전히 계산할 수 없으니 (모든 trajectory를 고려할 수 없으니), sample trajectory 몇 개에 대해서만 계산한 것으로 expectation을 근사한 값을 추정하게 되는데, 이 때 trajectory의 경우의 수가 너무 많기 때문에 그렇습니다. Variance가 큰게 문제인 이유는 뭘까요?
 Slide. 14.
Slide. 14.
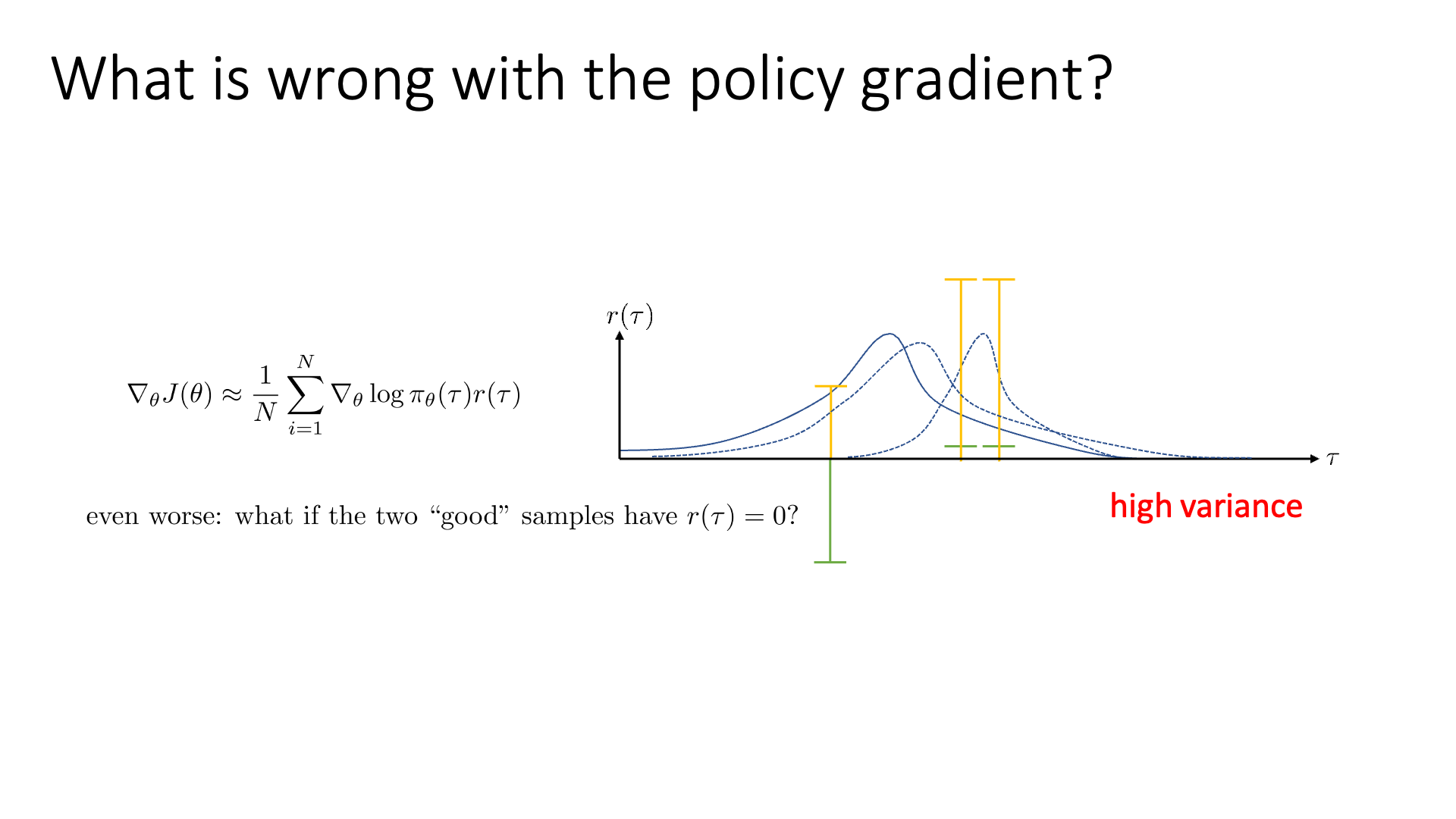
Slide 14의 example을를 봅시다. x축은 all possible trajectories를 의미하며 y축은 해당 각 trajectory가 sampling될 확률을, 그리고 녹색, 노란색 기둥은 return을 의미합니다. 우리가 3개의 trajectory를 sampling 했더니 녹색의 reward를 얻었다고 생각해봅시다.
VPG의 수식과 직관에 따라서 우리는 negative reward를 return하는 trajectory는 덜 일어나게끔 하고, 조금이라도 positive reward를 return하는 trajectory는 장려하게 됩니다.
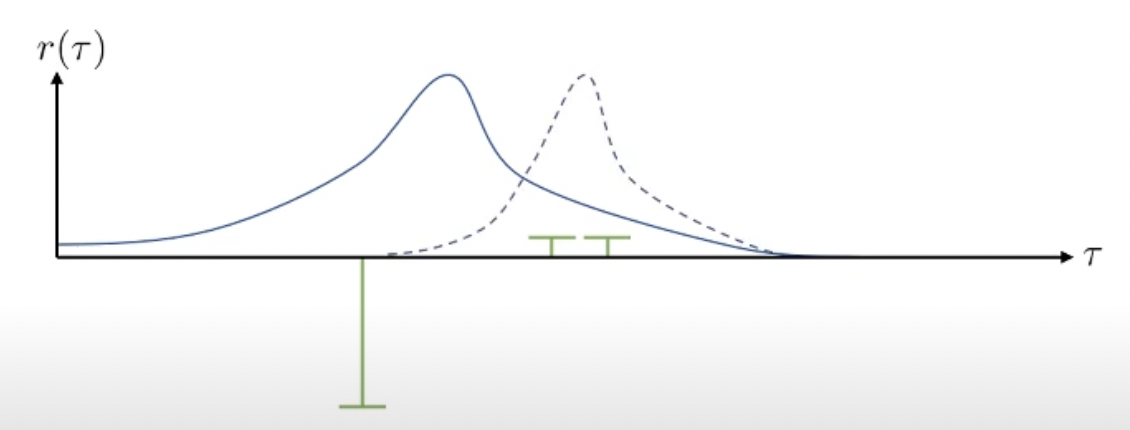
그 결과 위와 같이 policy가 업데이트 되어 trajectory distibution이 변화했습니다 (오른쪽으로 많이 움직였습니다). 매우 큰 negative reward를 받는 trajectory는 완전히 확률이 0에 가까워 졌습니다.
그런데 RL simulation 환경에서는 여러 이유로 (environment의 stochasticity라던가) 같은 trajectory도 다른 reward를 받을 수도 있습니다. 이번에는 각 trajectory의 return에 공평하게 어떤 양수를 더해봅시다. (이렇게 극단적으로 차이나는 경우는 거의 없겠지만? 예를 들어서)
MDP에서는 상수를 더하거나 해도 수식적으로 문제가 되지 않는다고 합니다 (optimal policy도 달라지지 않음). 그러므로 위의 수식에서 reward에 적당한 상수 (예를 들어 +100 씩)를 더하면 아래와 같은 그림을 얻을 수 있습니다.
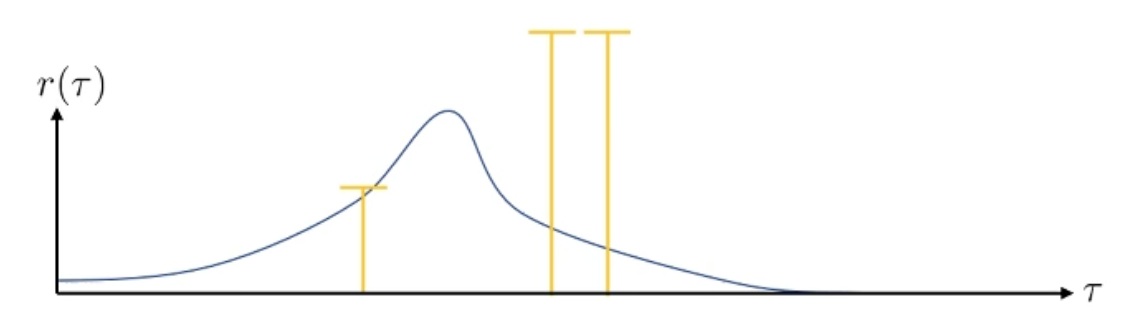
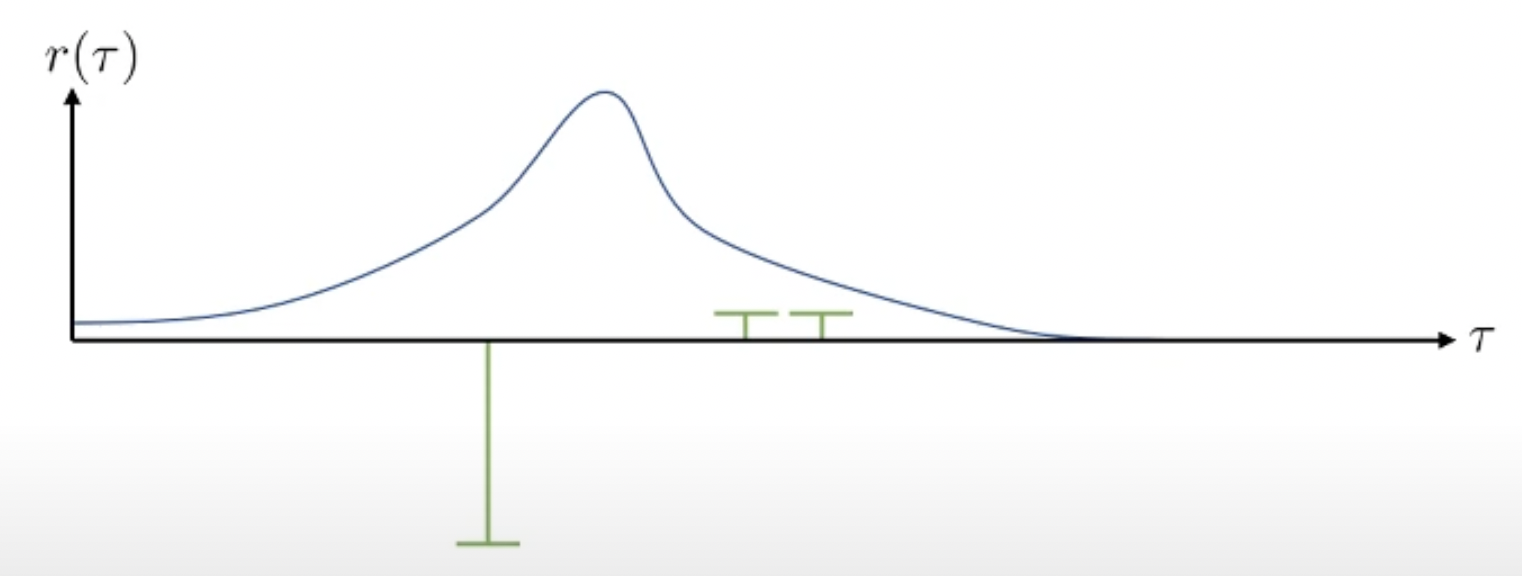
모두 +100을 해줬으니 이들의 상대적인 차이는 달라지지 않았습니다. 여전히 맨 왼쪽에 있는 trajectory는 매우 나쁜 sample이며, 오른쪽 2개는 좋은 sample들입니다. 하지만 이러한 경우 모든 trajectory가 좋게 평가되어 distribution이 거의 움직이지 않게 됩니다.
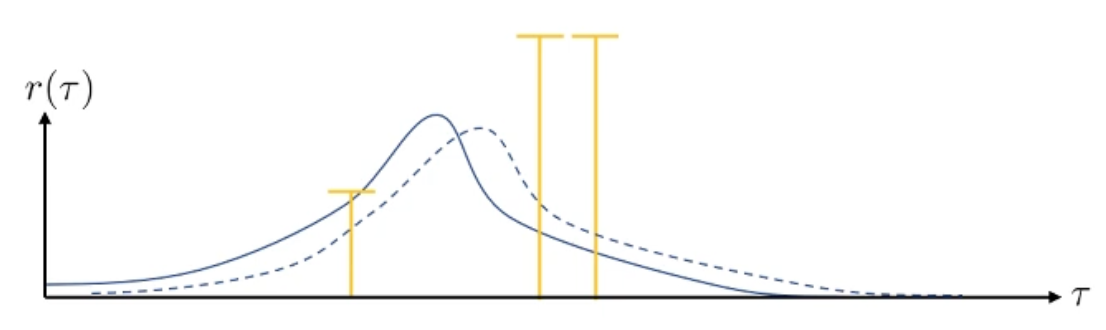
왜냐면 지금의 경우에는 절대적인 기준으로 봤을 때 bad trajectory는 없고 good trajectory만 있기 때문입니다. 모두 good trajectory라고 생각해서 확률이 다같이 올라가므로 거의 변하지 않는 것입니다. 만약 맨 오른쪽 두 sample들이 모두 0이되거나, 왼쪽 sample이 0이 되면 상황은 더 이상해질 수 있습니다.
이러한 문제는 우리가 기대값을 제대로 계산할 수 없어 sampling을 하기 때문에 발생하는 것이라 할 수 있겠습니다. Trajectory를 무한대에 가깝게 뽑으면 게중에는 bad trajectory나 good trajectory가 반드시 있을 것이기 때문에 문제가 되지 않을겁니다. 그런데 positive return의 trajectory만 뽑히더라도 어떤 trajectory는 상대적으로 bad trajectory이고 어떤 trajectory는 게 중에서도 good trajectory일 겁니다. 예를 들어 수학 문제를 푸는 agent가 점수를 잘 받았냐 못 받았냐를 평가해서 algorithm을 update 하려고 할 때, 50점이나 90점을 받은 trajectory들에 대해서 모두 확률을 높히는 것 보다는 평균 점수가 80점 이라면 이를 기준으로 policy를 update하는게 더 좋을겁니다.
(Variance가 크다는 것은 분포가 굉장히 넓어서, sampling을 하면 sample들이 천차만별로 다르게 뽑힐수도 있다는 걸 의미합니다. RL에서 variance가 크다는 것은 굉장히 많은 내용을 내포하고 있을 수 있는데, 예를 들어 후에 Actor-Critic algorithm에서는 \(s_t\)에서 \(a_t\)를 했을 때 그 action이 좋았는지?를 평가해야 하는데 이 평가를 현재 policy를 통해서 episode를 5번 정도 돌려본 결과값의 평균을 사용할 수 있습니다. 그런데 이 policy를 돌려본다는 것 자체가 stochastic 하기 때문에 매 번 5번 sampling을 해서 평균을 취할때마다 그 값이 달라지는 문제가 생길 수 있습니다. 이런것 또한 high variance하다고 할 수 있습니다)
 Slide. 15. review는 생략
Slide. 15. review는 생략
Applying Causality
Variance를 줄여봅시다. 이를 위해 이번 subsection에서는 두 가지가 제안됩니다.
- Causality
- Baseline
 Slide. 17.
Slide. 17.
Causality는 우리가 존재하는 universe에서 언제나 참인 명제로,
우리가 어떤 시점 \(t\)에서 한 행동이 미래(\(t < t'\))에 영향을 줄 지언정 과거(\(t' < t\))에는 영향을 줄 수 없다는 것을 의미합니다.
(중요한 점은 이것이 MDP랑 다르다는 겁니다.
MDP는 우리가 다루는 process에 따라서 참일수도 거짓일수도 있지만,
Causality는 언제나 참이라고 합니다)
이를 적용한 VPG는 아래와 같이 수정이 될 수 있습니다.
\[\begin{aligned} & \nabla_{\theta}J(\theta) \approx \sum_{i=1}^N ( \sum_{t=1}^T \nabla_{\theta} \log \pi_{\theta} (a_{i,t} \vert s_{i,t}) ) ( \sum_{t=1}^T r(s_{i,t},a_{i,t}) ) & \\ & \nabla_{\theta}J(\theta) \approx \sum_{i=1}^N ( \sum_{t=1}^T \nabla_{\theta} \log \pi_{\theta} (a_{i,t} \vert s_{i,t}) ) ( \sum_{ \color{red}{t'} =1 }^T r(s_{i,\color{red}{t'}},a_{i,\color{red}{t'}}) ) & \\ & \nabla_{\theta}J(\theta) \approx \sum_{i=1}^N ( \sum_{t=1}^T \nabla_{\theta} \log \pi_{\theta} (a_{i,t} \vert s_{i,t}) ) ( \sum_{ \color{red}{t'=t} }^T r(s_{i,\color{red}{t'}},a_{i,\color{red}{t'}}) ) & \\ \end{aligned}\]Causality가 working하는 이유는 굉장히 단순한데, reduced timestep에 대해서 expectation을 계산하는것이 variance가 더 작기 때문입니다.
여기서 앞으로 우리는 \(\sum_{t'=t}^T r(s_{i,t'},a_{i,t'})\)라는 quantity를 \(\color{red}{ \hat{Q_{i,t}} }\)로 따로 정의하고,
이를 Reward-to-go라고 부를 겁니다.
혹은 이를 Q라고 표기하기도 하는데, 이는 lecture 4에서 잠깐 언급된Q-Function와 같은겁니다.
Q값은 “현재 state에서 이 action을 했을 때 얻을 수 있는 기대 return의 값”을 의미했습니다.
Lecture 6에서 Actor-Critic algorithm을 유도할 때 다시 쓴다고 하니 넘어가도록 하겠습니다.
Applying Baseline
그 다음은 Baseline을 적용하는겁니다.
 Slide. 18.
Slide. 18.
이는 trajectory가 가지는 보상에 대한 평균인 (\(b = \frac{1}{N} \sum_{i=1}^N r(\gamma)\))를 기준삼아 이 평균 값 보다 더 좋은 trajecotry의 action들은 확률을 높히고, 그 반대는 낮추겠다는 걸 의미합니다. 이 때, 이 평균을 baseline이라고 부르고 모든 trajectory의 return에 공통적으로 빼주면 됩니다.
\[\begin{aligned} & \nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \nabla_{\theta} \log p_{\theta} (\tau) r(\tau) & \\ & \nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \nabla_{\theta} \log p_{\theta} (\tau) [ r(\tau) - \color{red}{ b } ] & \\ & \text{where } b = \frac{1}{N} \sum_{i=1}^N r(\tau) & \\ \end{aligned}\]매우 직관적입니다만 “이렇게 막 빼도 되는가?” 하는 생각이 들 수 있습니다. 하지만 baseline을 빼는 것이 variance에만 영향을 주고 여전히 원래의 expectation에는 영향을 주지 않는다는 것을 간단하게 증명할 수 있습니다.
\[\begin{aligned} & \nabla_{\theta} J(\theta) \approx \frac{1}{N} \sum_{i=1}^N ( \nabla_{\theta} \log p_{\theta} (\tau) r(\tau) - \color{red}{ \nabla_{\theta} \log p_{\theta} (\tau) \cdot b } ) & \\ & \frac{1}{N} \sum_{i=1}^N \nabla_{\theta} \log p_{\theta} (\tau) \cdot b = \int \nabla_{\theta} p_{\theta} (\tau) \cdot b \space d \tau = b \nabla_{\theta} \int p_{\theta} (\tau) d \tau = 0 & \\ \end{aligned}\]이런 trajecotry들의 return의 평균값을 baseline으로 쓰는 방법을 Constant Baseline이라고 하는데,
이것이 best는 아니지만 실제로 잘 작용한다고 합니다.
(실제로는 Q, V를 baseline으로 쓰는데, 이는 lecture 6에서 나옴)
그 다음으로 실제로 얼만큼 variance가 줄어드는지를 분석하고 optimal baseline이 무엇인지 계산을 합니다.
 Slide. 19.
Slide. 19.
Variance를 계산하는건 간단하죠.
\[Var[x] = \mathbb{E} [x^2] - \mathbb{E} [x]^2\]이를 RL objective 의 gradient에 적용해봅시다.
\[\begin{aligned} & \nabla_{\theta} J(\theta) = \mathbb{E}_{\tau \sim p_{\theta}(\tau)} [ \nabla_{\theta} \log p_{\theta} (\tau) (r(\tau) \color{red}{- b}) ] &\\ & Var = \mathbb{E}_{\tau \sim p_{\theta}(\tau)} [ ( \nabla_{\theta} \log p_{\theta} (\tau) (r(\tau) - b) )^2 ] & \\ & - \mathbb{E}_{\tau \sim p_{\theta}(\tau)} [ \nabla_{\theta} \log p_{\theta} (r(\tau) - b) ]^2 & \\ \end{aligned}\]그런데 여기서 두번째 항인 \(\mathbb{E}[x]^2\)에 해당하는 term은 unbias임을 이미 보였기 때문에 baseline을 적용하든 말든 같은 값을 return합니다. 그러니까 이건 constant인 것이고 첫 번째 term에 의해 variance가 dominate되게 됩니다. 첫 번째 term이 gradient (앞으로 \(g(\tau)\)라고 함)에 \(r(\tau)\)가 곱해지느냐 \((r(\tau) - b)\)가 곱해지느냐의 차이가 baseline이 가져다주는 차이인데, baseline을 빼는 것이 variance를 더 줄인다는 결론이 나게 됩니다.
그러면 어떤 baseline이 최적의 baseline인가? 이는 아래의 수식을 \(b\)에 대해서 미분해서 극값을 찾으면 알 수 있습니다.
\[\begin{aligned} & Var = \mathbb{E}_{\tau \sim p_{\theta}(\tau)} [ ( \nabla_{\theta} \log p_{\theta} (\tau) (r(\tau) - b) )^2 ] & \\ & = \mathbb{E}_{\tau \sim p_{\theta}(\tau)} [ g(\tau)^2 r(\tau)^2 ] - 2 \cdot \mathbb{E}_{\tau \sim p_{\theta}(\tau)} [ g(\tau)^2 r(\tau) \cdot \color{red}{b} ] + \color{red}{b^2} \cdot \mathbb{E}_{\tau \sim p_{\theta}(\tau)} [ g(\tau)^2 ] & \\ \end{aligned}\]즉 optimal baseline은 \(b = \frac{\mathbb{E}[g(\tau)^2 r(\tau)]}{\mathbb{E}[g(\tau)^2]}\)가 되는데, 이는 expected reward 이긴하나 gradient의 magnitude만큼을 weight 해준 값이 됩니다. RL algorithm을 실제로 구현하는 데 있어 잘 사용되지는 않지만 variance를 minimize하는 optimal baseline을 구할 수 있다는 점에 의의를 두면 될 것 같습니다.
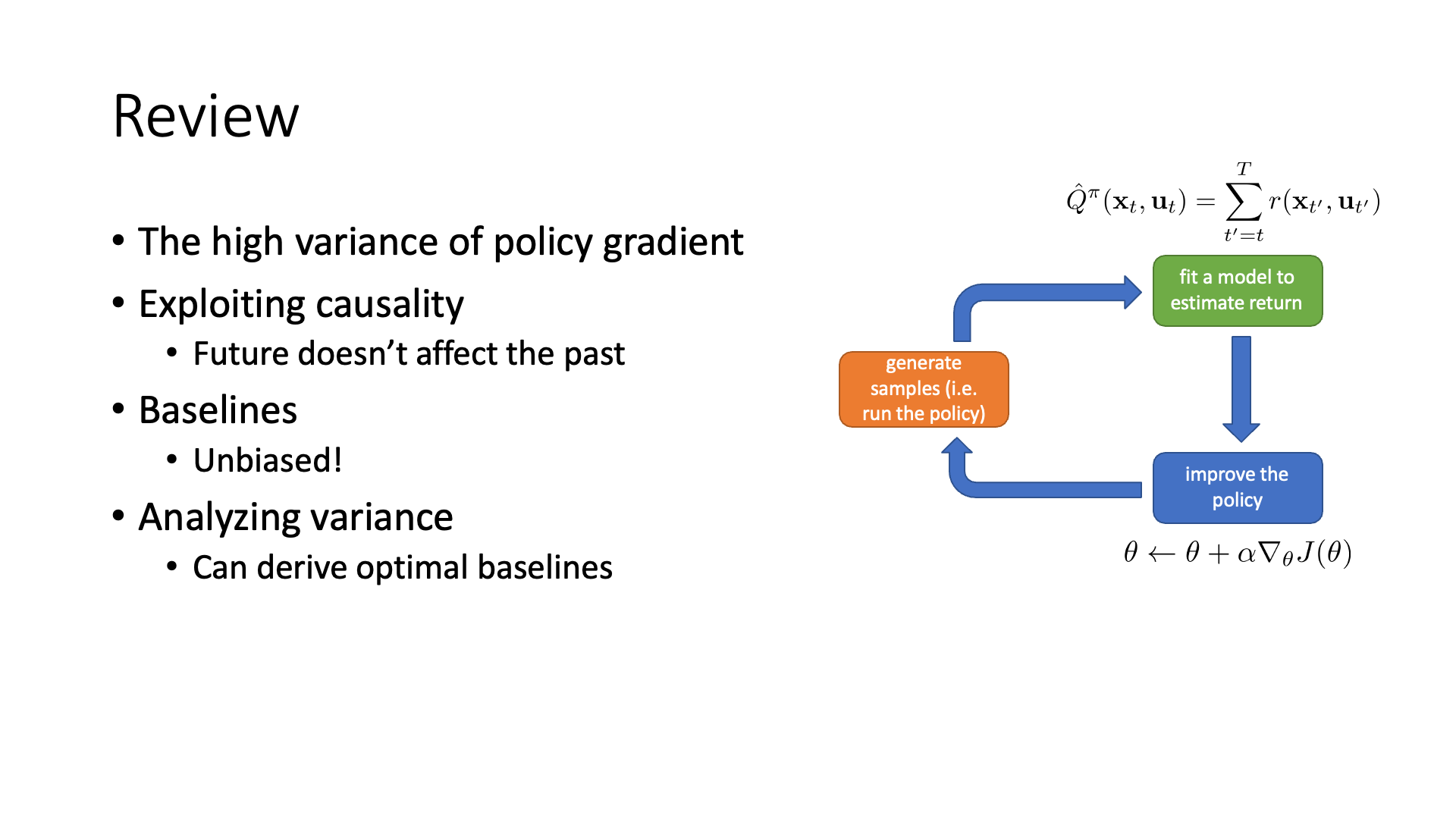 Slide. 20. review는 생략.
Slide. 20. review는 생략.
Off-Policy Policy Gradients
다음으로 알아볼 것은 Off-Policy setting 에서의 PG algorithm 입니다.
우리가 지금까지 알아본 VPG를 포함해 대부분의 RL algorithm은 On-Policy algorithm이라고 했었습니다.
 Slide. 22.
Slide. 22.
On-policy라는 것은 current policy을 update하기 위해 반드시 current policy가 뽑은 sample들을 써야한다는 걸 의미합니다. 가령 \(\pi_{100}\)으로의 update를 위해서는 \(\tau \sim \pi_{99}\)을 써야만 하고 \(\pi_{90}\)이 뽑은 것은 쓸 수 없는겁니다. 그 이유는 RL objective가 current policy하의 trajectory distribution 하의 return의 expectation을 maximize 하는 것이기 때문에 오래된 trajectory를 쓰는 것은 더 나은 policy가 된다는 것이 보장이 되지 않기 때문이라고 합니다 (수학적으로?).
하지만 gradient ascent로 parameter를 update해봐야 값이 조금씩 변할텐데 (parameter가 조금 변한다는 것은 policy도 조금 변한다는 것일 수 있음),
별로 변하지도 않은 policy 때문에 매번 sampling을 다시 해야 한다는 것 자체가 굉장히 부담스러울 수 있습니다.
그래서 이런 on-policy algorithm들은 좋은 policy를 얻기 위해 무수히 많은 sample이 필요하기 때문에,
이른 바 sample inefficient algorithm이라고 한다고 lecture 4에서 잠시 얘기했었습니다.
그럼 어떻게 좀 오래된 trajectory로, 더 극단적인 case로는 10 step이전의 policy도 아니고 아예 남들이 미리 학습해둔 policy로 부터 samplin한 trajectory로 학습할 수 있을까요? 이를 위해서 Importance Sampling (IS)라는 수학적 tool을 사용해 봅시다.
Off-Policy PG: PG with Importance Sampling
Importance Sampling (IS)는 간단히 말해 A라는 distribution 하에서의 expectation을 계산하는 경우에 대해,
B라는 distribution하에서 동일한 expectation을 계산할 수 있도록 해주는 technique 입니다.

이 수식에서 approximation이 들어간 것은 하나도 없기 때문에 IS는 unbiased 수식입니다. 이를 VPG에 적용해봅시다.
 Slide. 23.
Slide. 23.
원래의 RL objective는 다음과 같았습니다.
\[J(\theta) = \mathbb{E}_{\tau \sim p_{\theta}(\tau)} [r(\tau)]\]그런데 우리는 \(\color{red}{\bar{p}(\tau)}\)라는 trajectory distribution에서 sampling을 하고 싶습니다.
\[J(\theta) = \mathbb{E}_{\tau \sim \color{red}{\bar{p}(\tau)}} [ \frac{p_{\theta} (\tau)}{\color{red}{\bar{p}(\tau)}}r(\tau) ]\]Trajectory를 current policy가 아닌 \(\color{red}{\bar{p}(\tau)}\)에서 뽑았기 때문에 reward를 계산할 때 그만큼의 확률 보정을 해준 것이죠. 이제 앞서 많이 했던 것 처럼 trajectory distribution을 factorization 해서 두 distribution로 구성된 importance weight을 전개하면 역시나 우리는 dynamics, \(p(s_{t+1} \vert s_t, a_t)\)를 알 필요가 없습니다.
 Slide. 24.
Slide. 24.
한 편, VPG를 importance sampling을 통해서 유도할 수도 있습니다. 만약에 current policy가 \(\theta\)로 parameterize 되어있고, PG를 통해 update될 parameter를 \(\theta'\)라고 해 봅시다. 이 때 \(\theta'\)의 policy를 굴렸을 때의 return의 기대값인 RL objective를 다음과 같이 쓸 수 있습니다.
\[\begin{aligned} & J(\theta') = \mathbb{E}_{\tau \sim p_{\theta'}(\tau)}[r(\tau)] & \\ & = \mathbb{E}_{\tau \sim p_{\theta}(\tau)}[\frac{ p_{\theta'}(\tau) }{ p_{\theta}(\tau)} r(\tau)] & \\ \end{aligned}\]이제 이 IS version의 objective를 \(\theta'=\theta\)인 지점에 대해서 미분을 해 봅시다.
\[\nabla_{\theta'} J(\theta') = \mathbb{E}_{\tau \sim p_{\theta}(\tau)}[ \frac{ \nabla_{\theta'} p_{\theta'}(\tau) }{ p_{\theta}(\tau)} r(\tau) ]\]그러면 우리는 importance weight의 미분체가 아래의 chain rule에 따르기 때문에, IS version의 RL objective의 graident 또한 사실상 VPG와 동일하다는 걸 알 수 있습니다.
\[\begin{aligned} \nabla_{\theta'} \log f(\theta') \vert_{\theta' = \theta} = \frac{ \nabla_{\theta'} f(\theta') \vert_{\theta' = \theta} }{ f(\theta) } = \nabla_{\theta'} ( \frac{ f(\theta') }{ f(\theta) }) \vert_{\theta' = \theta} \end{aligned}\]하지만 우리가 원하는건 \(\theta' = \theta\)인 경우에 대해서가 아니죠. 즉 몇 step 이전의 trajectory를 사용해서 RL objective의 현재 policy에 대한 gradient를 구하는 겁니다. 다시 \(p_{\theta}(\tau) \nabla_{\theta} \log p_{\theta}(\tau) = \nabla_{\theta} p_{\theta}(\tau)\) 라는 identity를 이용해서 RL objective의 gradient를 re-writing 해봅시다.
\[\nabla_{\theta'} J(\theta') = \mathbb{E}_{\tau \sim p_{\theta}(\tau)}[ \frac{ p_{\theta'}(\tau) }{ p_{\theta}(\tau)} \nabla_{\theta'} \log p_{\theta'}(\tau) r(\tau) ]\] Slide. 25.
Slide. 25.
이제 이 gradient를 좀 더 풀어봅시다.
\[\nabla_{\theta'} J(\theta') = \mathbb{E}_{\tau \sim p_{\theta}(\tau)}[ \color{red}{ \frac{ p_{\theta'}(\tau) }{ p_{\theta}(\tau)} } \nabla_{\theta'} \log p_{\theta'}(\tau) r(\tau) ]\]Expectation에 있는 importance weight, \(\frac{ p_{\theta'}(\tau) }{ p_{\theta}(\tau)}\)를 앞서 했던 것 처럼 factorization을 해 봅시다. 그러면 단순히 action distribution의 product로 바뀝니다.
\[\nabla_{\theta'} J(\theta') = \mathbb{E}_{\tau \sim p_{\theta}(\tau)}[ \color{red}{ (\prod_{t=1}^T \frac{ \pi_{\theta'}(a_t \vert s_t) }{ \pi_{\theta}(a_t \vert s_t) }) } ( \sum_{t=1}^T \nabla_{\theta'} \log \pi_{\theta'}(a_t \vert s_t) ) ( \sum_{t=1}^T r(s_t,a_t) ) ]\]여기서 \((\prod_{t=1}^T \frac{ \pi_{\theta'}(a_t \vert s_t) }{ \pi_{\theta}(a_t \vert s_t) })\)를 Causality를 사용해서 적절히 분배하면 아래와 같은 수식을 얻을 수 있습니다.
\[\begin{aligned} & \nabla_{\theta'} J(\theta') = \mathbb{E}_{\tau \sim p_{\theta}(\tau)}[ \color{red}{ ( \prod_{t=1}^T \frac{ \pi_{\theta'}(a_t \vert s_t) }{ \pi_{\theta}(a_t \vert s_t) }) } ( \sum_{t=1}^T \nabla_{\theta'} \log \pi_{\theta'}(a_t \vert s_t) ) ( \sum_{t=1}^T r(s_t,a_t) ) ] & \\ & \nabla_{\theta'} J(\theta') = \mathbb{E}_{\tau \sim p_{\theta}(\tau)}[ ( \sum_{t=1}^T \nabla_{\theta'} \log \pi_{\theta'}(a_t \vert s_t) ) \color{blue}{ (\prod_{t'=1}^t } \frac{ \pi_{\theta'}(a_{t'} \vert s_{t'}) }{ \pi_{\theta}(a_{t'} \vert s_{t'}) }) ( \sum_{t=1}^T r(s_t,a_t) ) \color{green}{ (\prod_{t''=t}^{t'} } \frac{ \pi_{\theta'}(a_{t''} \vert s_{t''}) }{ \pi_{\theta}(a_{t''} \vert s_{t''}) }) ] & \\ \end{aligned}\]수식의 의미를 생각해봅시다. 직관적으로 우선 \(t\)시점의 action, \(a_t\)에 대해서, 이는 몇 step 전의 policy를 따르는 trajectory의 action 중 하나일텐데, 실제로 policy가 update를 통해 많이 달라졌다면 됐다면 각 state에서 각 action을 할 확률이 변했을 겁니다. 이를 보정해준 것이라고 볼 수 있는데, trajectory가 진행될수록 distributional shift가 많이 일어났을 것이기 때문에 누적해서 곱해주는 걸 의미할겁니다. 그 다음은 \(s_t\)에서 \(a_t\)를 했을 때 그 이후 얻게 될 total reward의 expectation인데, 이것도 현재 policy를 따르는 것이 아니기 때문에 비율을 조정해준 것이죠.
이제 모든게 문제가 없어보이고 계산하면 될 것 같지만,
reward와 곱해지는 term, \((\prod_{t''=t}^{t'} \frac{ \pi_{\theta'}(a_{t''} \vert s_{t''}) }{ \pi_{\theta}(a_{t''} \vert s_{t''}) })\)가 문제가 된다고 합니다.
Sergey는 일단 이를 무시하자고 하는 것 같은데,
이 term을 무시하게 되면 lecture 7에서 배울 Policy Iteration이라고 하는 algorithm이 된다고 합니다.
지금은 와닿지 않을 수 있지만 policy iteration algoritm은 iteration 마다 policy improvement가 보장된(?) algorithm이라고 하며 곧 자세하게 다룰 거라고 합니다.
어쨌든 두 번째 ratio는 일단 무시하고 생각해보자는 것 같은데, 첫 번째 ratio은 그럴 수 없다고 합니다. 그리고 첫 번째 importance weight는 대체로 1보다 작은데, 이를 여러번 곱하다보면 0에 수렴하게 되어 문제가 된다고 합니다. 이는 make sense한데, 왜냐하면 sasmpled action이 \(\theta\)를 따를 것이기 때문에 \(\pi_{\theta}(a_t \vert s_t)\)가 훨씬 정교한? 높은 확률을 return할 것이기 때문입니다. Sergey는 이를 두고 가뜩이나 VPG는 high variance algorithm인데 여기에 high variance인 importance weight을 곱함으로써 gradient의 variance를 굉장히 빠르게 무한대로 발산시킨다고 합니다.
 Slide. 26.
Slide. 26.
그래서 당연히 첫 번째 ratio term도 제거를 해야됩니다 (그런데 당연히 수렴성을 해치지는 말아야겠죠).
On-Policy의 경우를 다시 생각해보겠습니다.
이를 state action marginal으로 생각해봅시다.
Trajectory는 각 timestep, \(t\)의 state action marginal distribution인 \(\pi_{\theta}(s_t, a_t)\)에서 \((s_t,a_t)\)를 (set로) sampling한 것이 됩니다.
Off-Policy도 state-action marginal을 이용해 re-writing하면 다음을 얻을 수 있다고 합니다.
(아마 다시 수식을 유도해야 하는듯?)
하지만 이 수식 자체로는 쓸모가 없는데, 그 이유는 timestep, \(t\)에서의 state action marginal distribution, \(\frac{ \pi_{\theta'}(a_{i,t} s_{i,t}) }{ \pi_{\theta}(a_{i,t} s_{i,t}) }\)를 계산하기 위해서는 결국 state transition probability와 initial state distribution 등을 알아야 하기 때문이라고 합니다. 다만 이 수식을 chain rule등을 이용해 아래와 같이 표현할 수 있습니다.
\[\begin{aligned} & \nabla_{\theta'}J(\theta') \approx \frac{1}{N} \sum_{i=1}^N \sum_{t=1}^T \color{red}{ \frac{ p_{\theta'} (s_{i,t}) }{ p_{\theta} (s_{i,t}) } } \frac{ \pi_{\theta'}(a_{i,t} \vert s_{i,t}) }{ \pi_{\theta}(a_{i,t} \vert s_{i,t}) } \nabla_{\theta} \log \pi_{\theta} (a_{i,t} \vert s_{i,t}) \hat{Q_{i,t}} & \\ \end{aligned}\]이 수식이 의미하는 바는 timestep, \(t\)에 agant가 모든 state에 대해서 존재할 확률 \(p(s_t)\)를 알고, 그 때의 action distribution을 알면 (이건 model이 알려주므로 당연히 알 수 있음) 되는데, 문제는 \(p(s_t)\)를 알 수가 없다는 겁니다. (why? transition probability 모르니까, 우리는 단지 trial and error로 sampling해서 optimization만 할 줄 알지, environment가 어떻게 생겼는지 modeling한 적이 없음)
여기서 유일한 골칫거리인 \(\frac{ p_{\theta'} (s_{i,t}) }{ p_{\theta} (s_{i,t}) }\)을 무시할 수 있다면 어떻게 될까요? 그러면 우리는 다음의 매우 간단한 수식을 얻게 됩니다.
\[\nabla_{\theta'}J(\theta') \approx \frac{1}{N} \sum_{i=1}^N \sum_{t=1}^T \color{blue}{\frac{ \pi_{\theta'}(a_{i,t} \vert s_{i,t}) }{ \pi_{\theta}(a_{i,t} \vert s_{i,t}) } } \nabla_{\theta} \log \pi_{\theta} (a_{i,t} \vert s_{i,t}) \hat{Q_{i,t}}\]물론 여기서 많은 approximation이 들어갔기 때문에 이런 수식으로 얻은 policy는 나쁠수도 있습니다. 하지만 곧 이것이 특정 조건만 만족한다면 꽤 괜찮다는 것을 배우게 된다고 합니다.
언제 괜찮은가?
직관적으로 \(p(s_t)\)가 별로 다르지 않을 때 일겁니다.
그렇다면 state distribution이 별로 다르지 않을 때는 언제인가?
그건 바로 policy가 별로 다르지 않을 때가 될 수도 있고 … 어떤 특정 조건이 성립할 때 이며, 이는 lecture 9에서 자세하게 배우게 될 것입니다.
Implementing Policy Gradients
이번 subsection는 VPG를 실제로 pytorch와 같은 framework를 통해 구현하는 방법에 대해 얘기합니다. 그냥 MSE나 CE Loss에 reward를 곱해주고 (q value), pytorch의 auto-diff를 쓰면 된다고합니다. (너무 trivial해서 넘어가도록 하겠습니다)
 Slide. 30.
Slide. 30.
 Slide. 31.
Slide. 31.
(gradient가 noisy하고 learning rate가 중요하다는 말은 중요한 말이긴 합니다)
Advanced Policy Gradients
마지막 subsection입니다. 이 부분은 어차피 lecture 9에서 심도깊게 다룰 것이기 때문에 적당히 느낌만 보도록 하겠습니다.
 Slide. 34.
Slide. 34.
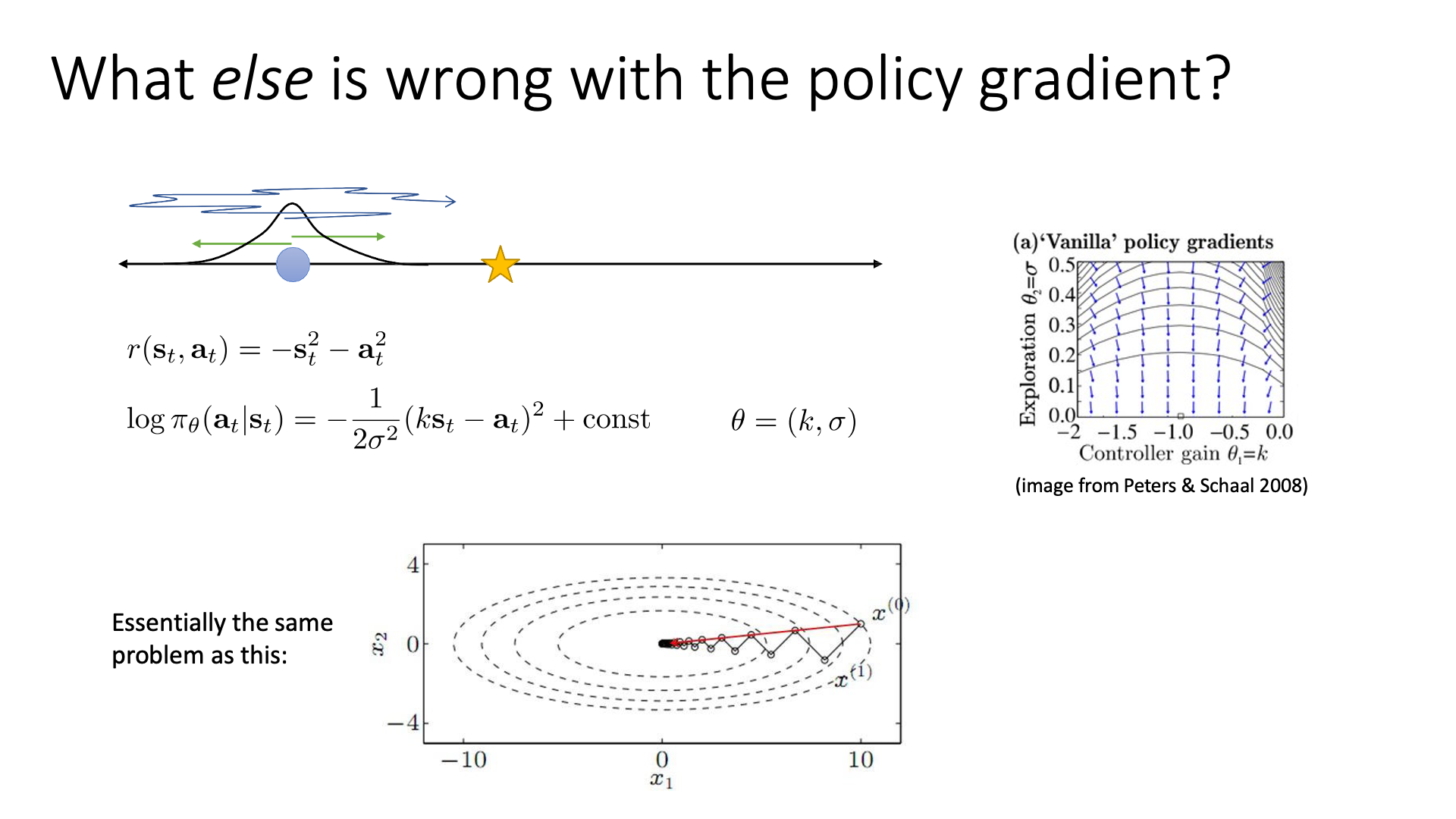
간단한 example를 하나 생각해보도록 하겠습니다. 위 slide에 나와있는것 처럼 수평선에 파란색 원점에서 출발하여 목적지 (star sign)에 도착하는 task에 대해서 생각해 보도록 하겠습니다. state도 1차원이며 action도 1차원 (action이라 할것이 왼쪽, 오른쪽 뿐이기 때문) 일겁니다. 이제 보상을 다음과 같이 정의해 봅시다.
\[r(s_t,a_t) = -s_t^2 -a_t^2\]즉 학습을 하면 목표지점에 멀어질수록 penalty가 곱해져 그런 action은 지양하게되고, 가까워질수록 그런 action은 지향하게 됩니다. Action space를 gaussian distribution이라고 가정하면 아래의 MSE loss를 얻을 수 있습니다.
\[\log \pi_{\theta} (a_t \vert s_t) = -\frac{1}{2\sigma^2} (\color{blue}{k} s_t - \color{blue}{a_t})^2 + const\]여기서 policy를 결정짓는 parameter는 mean, variance에 관여하는 \(\color{blue}{ k,\sigma }\) 두 가지 입니다. 이렇게 modeling된 VPG가 어떻게 수렴하는지는 slide의 오른쪽 상단에 있는 vector field을 보면 된다고 하는데, 주의깊게 봐야할 점은 vector들이 optimal point를 향하지 않는다는 겁니다. 그 이유는 optimal value인 \(\color{red}{k=-1.0,\sigma=0.0}\)에 가까워질수록, 즉 \(\sigma\)가 작아지면 작아질수록 \(\sigma\)에 대한 gradient가 커지기 때문입니다. 그렇기 때문에 수렴하기에 한세월이 걸린다고 합니다. (\(\sigma\)에 대해서 미분을 해보면 0에 가까울수록 커짐을 알 수 있다. gradient vector들은 길이로 normalize를 해서 unit length를 갖는 모양인데 \(\sigma\)의 편미분이 매우 크기 때문에 0부근에서는 화살표가 수직으로 보이는 것)
이 문제를 해결하기 위해서는 gradient를 계산할 때 \(\sigma\)를 re-scale을 해주면 되는데, 다시 말해서 서로 다른 parameter에 대해서 다른 scaling을 해주는 겁니다.
이는 우리가 예를 들어서 \(\parallel Ax - b\parallel^2\)같은 quadratic problem을 풀 때, matrix \(A\)의 eigenvalue들의 ratio가 너무 커서 ellipse의 shape이 원형에서 멀어질수록 optimization하기 어려운 것과 같은 문제를 말합니다. (즉 그냥 gradient descent할 때 feature들이 unnormalize되었다던가 하면 optimization하기 어려운 것을 말하는 듯)
 Slide. 35.
Slide. 35.
즉 어떤 parameter는 policy를 update 하는데 영향을 많이 끼치고 (둔감함),
어떤 parameter는 민감하므로 (위의 예시에서는 \(\sigma\)),
policy에 민감한 parameter는 small learning rate를 적용하고 그 반대는 large learning rate를 적용하는 겁니다.
어떻게 이렇게 할 수 있을까요? Lecture 9에서 자세히 다루겠지만 살짝만 얘기해봅시다. 먼저 gradient descent (혹은 ascent)를 constraint optimization으로 생각해 보는 것이 중요합니다. Gradient descent를 한다는 것은
\[\theta \leftarrow \theta + \alpha \nabla_{\theta} J(\theta)\]사실 아래의 constraint optimization을 푸는 것과 같습니다. 말로 풀어쓰면 “현재 parameter point에서 반경 \(\epsilon\)내의 parameter 후보군들 중, objective를 가장 minimize할 수 있는 parameter를 골라 그것으로 update한다” 입니다.
\[\begin{aligned} & \theta' \leftarrow \arg \max_{\theta'} (\theta' - \theta)^T \nabla_{\theta} J(\theta) & \\ & \text{ s.t. } \parallel \theta' - \theta \parallel^2 \leq \epsilon \\ \end{aligned}\]이 constraint optimization을 objective에 대해서 1st order taylor approximation 하고, constraint에 대해서는 2nd order approximation을 해서 lagrangian multipler로 풀면 gradient descent의 수식을 완전히 recover할 수 있습니다.
 Fig.
Fig.
하지만 parameter, \(\theta\) space 에서의 euclidean constraint은 별로 좋은게 아닙니다.
왜냐하면 각 parameter가 policy에 끼치는 영향이 다르기 때문이죠.
이러한 constraint을 신뢰 구간 (Trust Region)이라고 하고 constraint 이 포함된 objective function 으로,
원래 objective function을 근사한 것을 대리 손실 함수 (Surrogate Loss Function)이라고 부르는데 만약에 constraint가 잘못돼서 surrogate function을 잘못 고르게 되면 실제 loss function의 optimum으로부터 멀어지면서 겉잡을 수 없게 policy가 망가져버릴 수도 있을 겁니다.
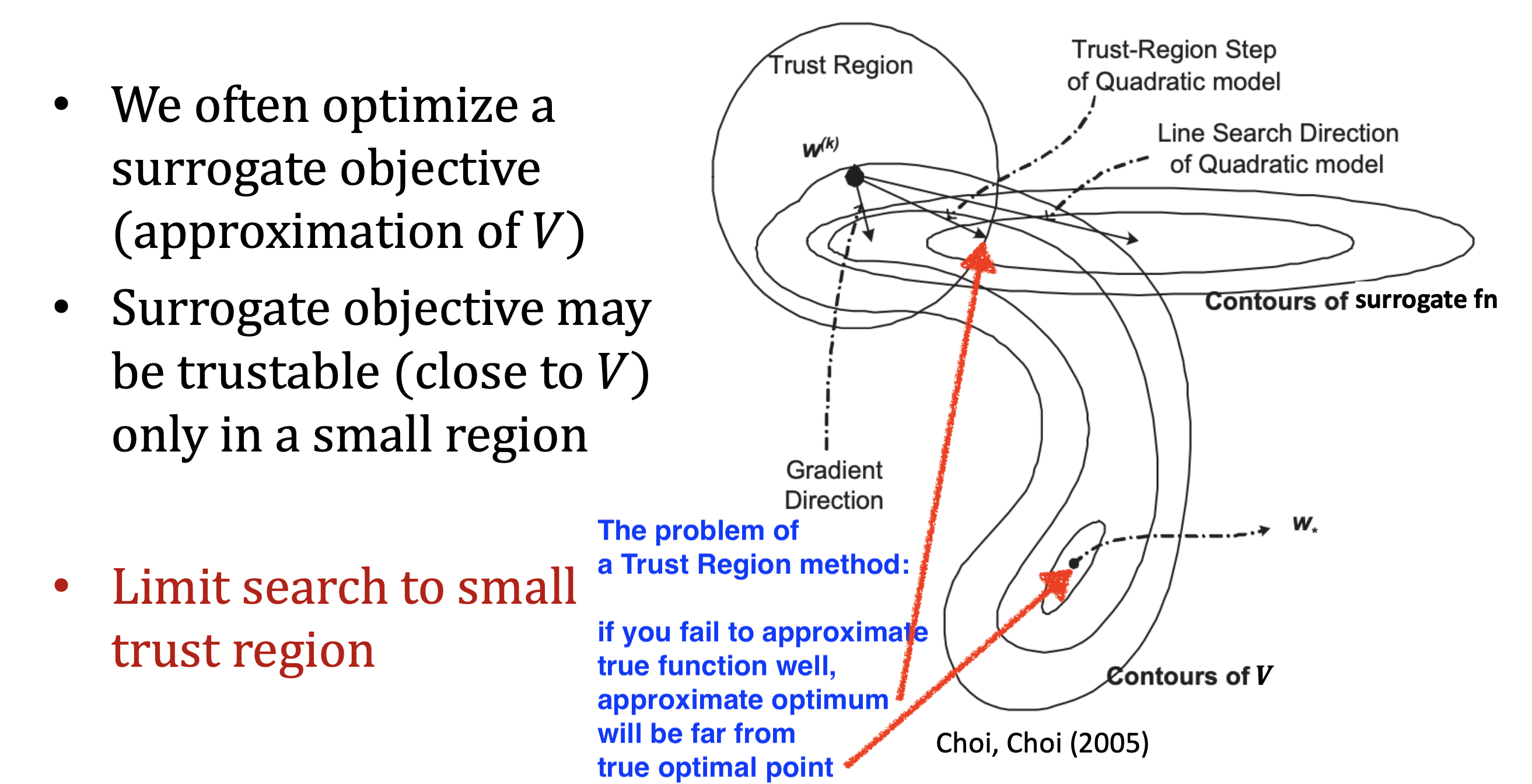 Fig. Source from CS885 by Pascal Poupart
Fig. Source from CS885 by Pascal Poupart
그럼 어떤 space에서의 constraint을 걸어줘야 할까요?
Solution은 'constraint을 parameter space에서 정의 하지 말고 policy space에서 정의하자' 입니다.
원래의 constraint optimization은 \(\parallel \theta' - \theta \parallel^2 \leq \epsilon\)에 의해서 'parameter 값을 크게 바꾸지 않는 선에서 최대로 update하자' 였다면,
지금의 constraint, \(D(\pi_{\theta'}, \pi_{\theta})\)를 적용한 optimization은 'parameter 값이 실제로 얼마나 변하든 상관없고 policy가 많이 변하지 않는 선에서 최대한 update하자'가 됩니다.
즉 어떤 parameter는 policy를 바꾸는데 크게 영향을 끼치지 않아서 100배정도 scale up해도 되면 그렇게 해도 된다는겁니다.
마지막으로 두 distribution의 similarity를 measure하는 것은 Kullback Leibler Divergence (KLD)을 사용하면 되는데,
이를 사용해서 최종적으로 optimization 수식을 다음과 같이 얻을 수 있습니다.
이 수식의 유도 과정과 타당성은 lecture 9에서 다시 나오기 때문에 어렵다면 대략적인 이해만 하고 넘어가셔도 됩니다. (유도하는 방법은 대충 largrangian multipler로 constraint optimization을 penalized optimization으로 바꾸고, objective에 대해서는 1st order taylor approximation을, penalty에 대해서는 2nd order taylor approximiaton을 해서 유도된 최종 수식의 극값을 찾으면 된다)
 Slide. 36.
Slide. 36.
이렇게 단순히 \(F^{-1}\) term (\(F\)는 Fisher Information)을 추가한 것 만으로도 slide 36에 나와있는것처럼 vector field를 nice하게 바꿀 수 있다고 합니다.
이제 더이상 optimal point에서 converge를 위해 영겁의 시간을 들이지 않아도 됩니다.
이를 Covariant or Natural policy gradient라고 부릅니다.
왜냐하면 KLD term을 2nd order approximation한 것은 \((\theta' - \theta)^T \color{red}{F} (\theta' - \theta)\)이기 때문에,
사실상 constraint이 아래처럼 원래의 radius가 \(\epsilon\)인 euclidean space를 선형 변환하기 때문입니다.
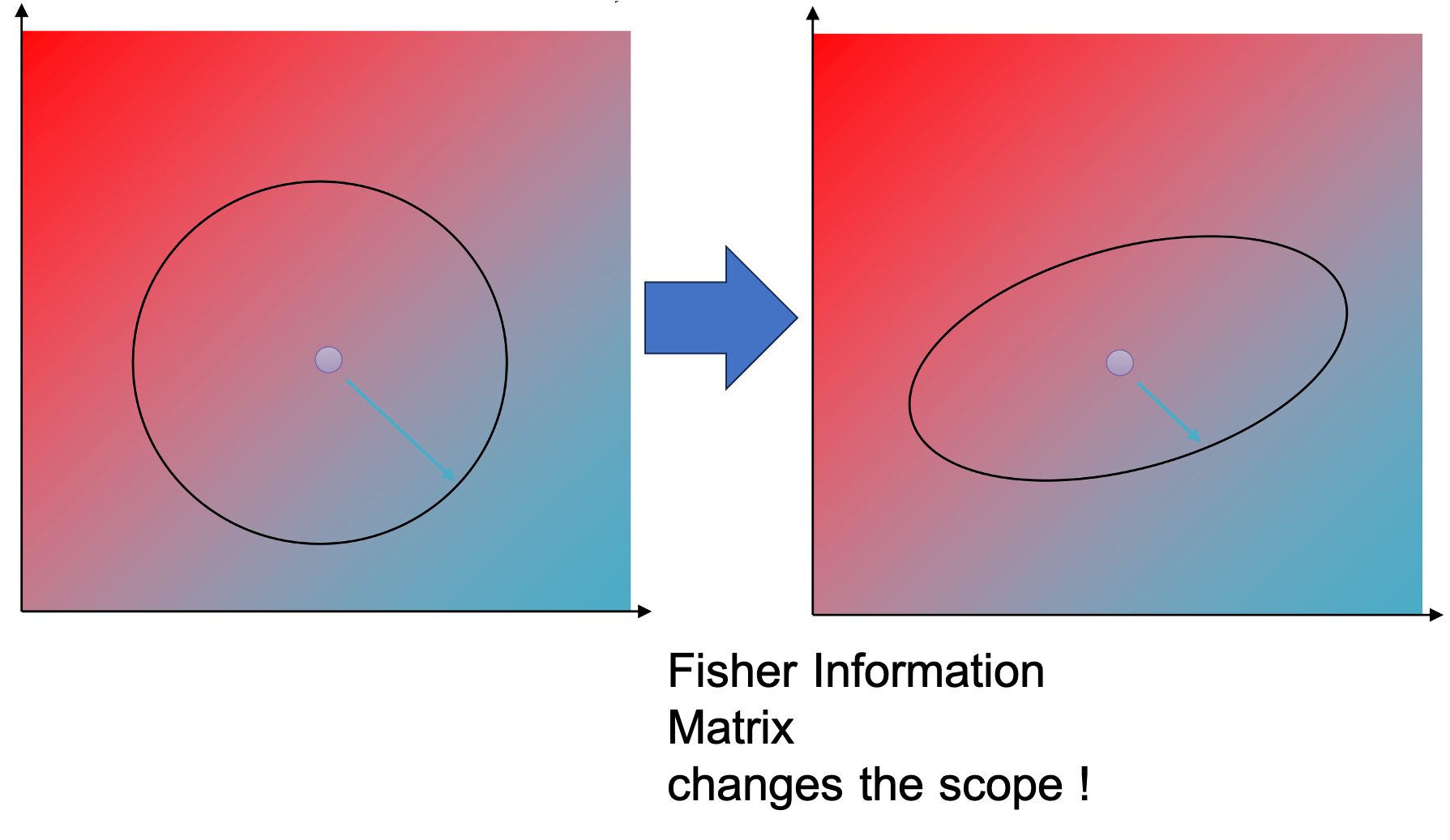 Fig. 변환된 euclidean constraint. 음영은 objective value를 의미한다.
Fig. 변환된 euclidean constraint. 음영은 objective value를 의미한다.
2002년에 제안된 Natural Policy Gradient (NPG)에서는 step size, \(\alpha\)까지 구하게 됩니다. 여기에 full fisher matrix를 구하는것이 아니라 fisher vector를 구해 연산량을 줄이고 line search등을 추가하면 2015년에 publish된 Trust Region Policy Optimization (TRPO)가 되며, 이를 좀더 simplify 한 것이 바로 Proximal Policy Optimization (PPO)입니다. PPO는 performance와 stability (convergence) 모두 훌륭하기 때문에 policy optimization based method의 standard이며 Large Language Model (LLM)의 학습 pipeline인 Reinforcement Learning From Human Feedback (RLHF)의 core learning algorithm입니다.
Examples
이하는 간단한 예시들과 읽을만한 paper list 입니다. Importance Sampling (IS)를 적용한다는 것은 Off-policy를 하겠다는 것이고, paper list에 있는 Natural Gradient나 TRPO등은 모두 lecture 9에서 자세히 다룰 예정이니 시간이 되는 분들만 미리 읽어보시면 좋을 것 같습니다.
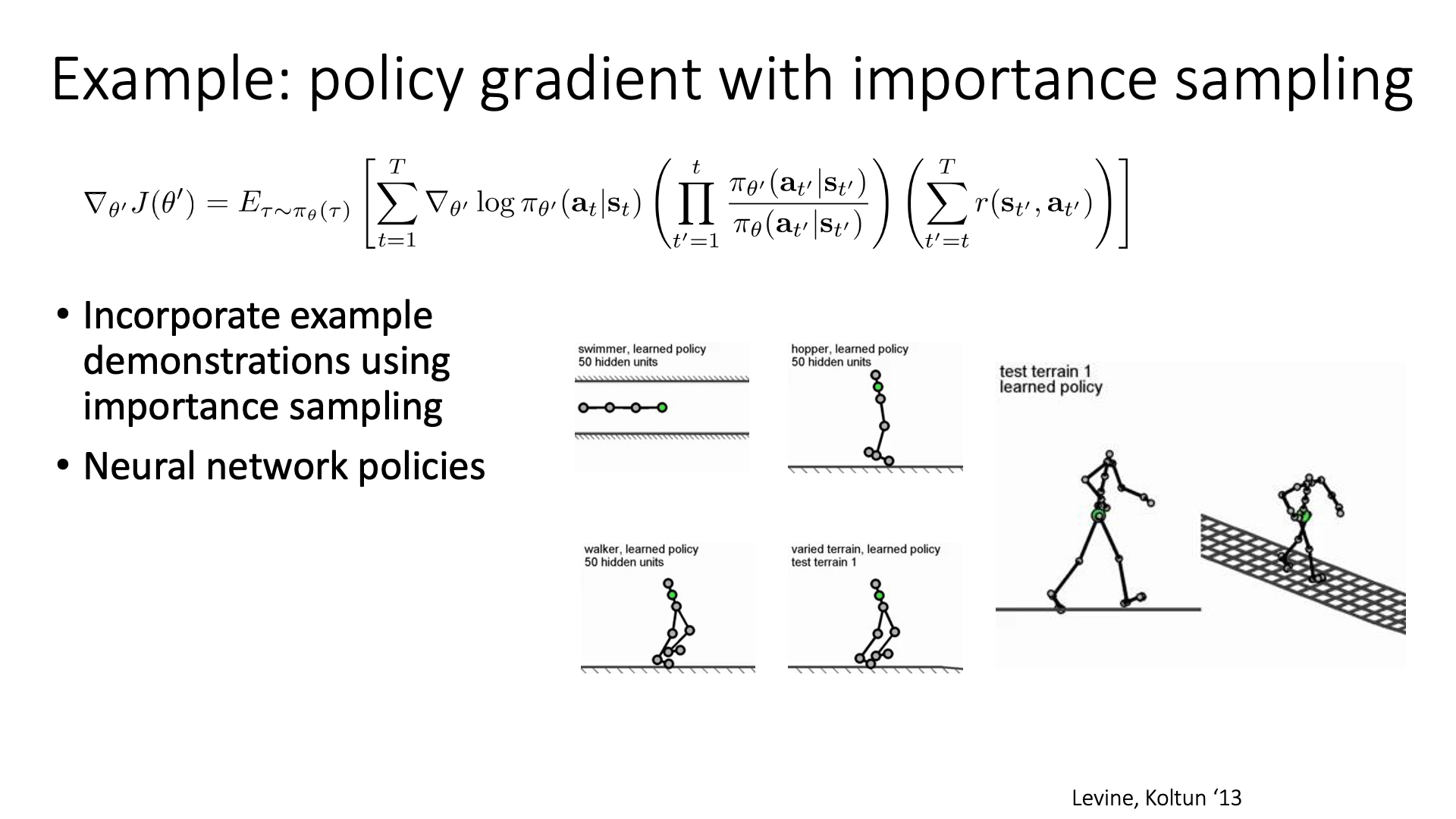 Slide. 38.
Slide. 38.
 Slide. 39.
Slide. 39.
 Slide. 40.
Slide. 40.
Outro
Lecture 6에서는 V, Q function이 VPG에 추가되는 것이 어떻게 variance를 줄이는가에 대해서 다룰 것이라고 합니다.
 Slide. 37.
Slide. 37.
추가적으로 lecture 5를 마친 현재 Deeo RL의 algorithm들 중 어디까지 봤으며, 앞으로 봐야할 것은 무엇인지에 대해 궁금하실 것 같아 자료를 준비했습니다.
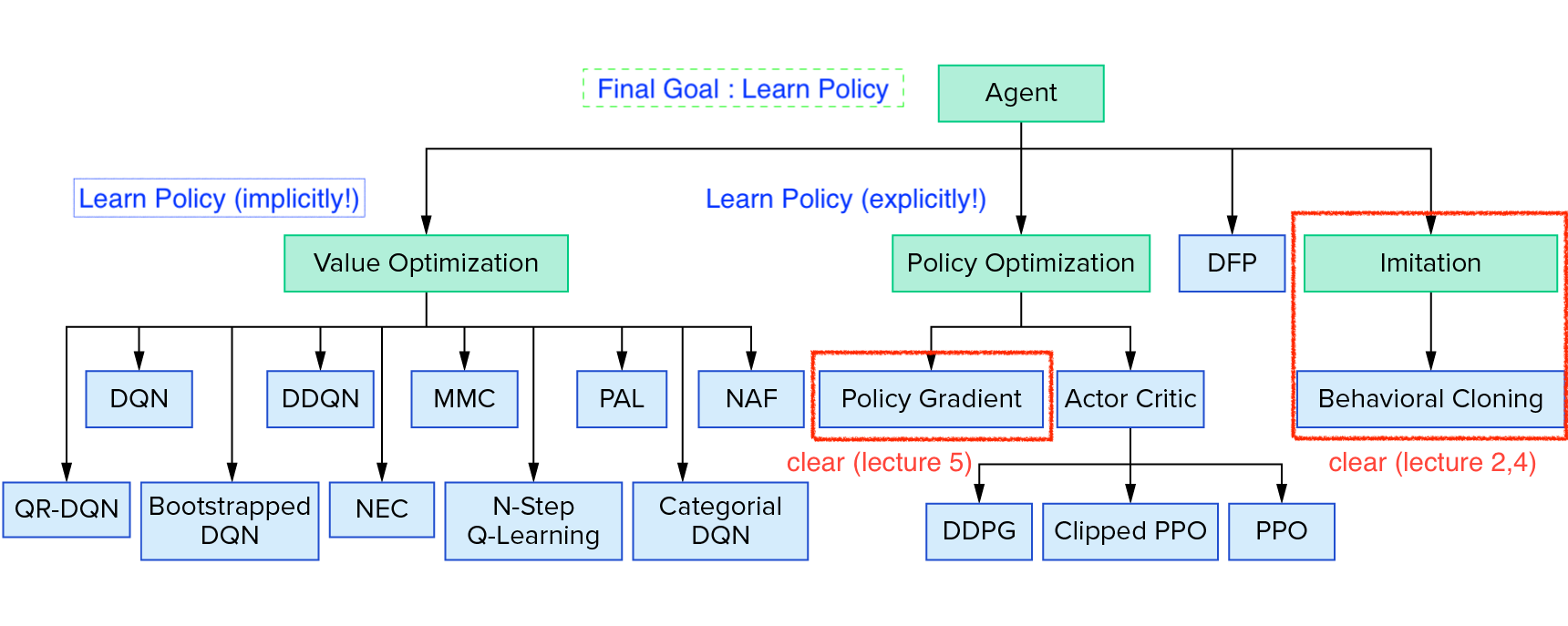 Fig. Reinforcement Learning Coach from Intel Lab
Fig. Reinforcement Learning Coach from Intel Lab
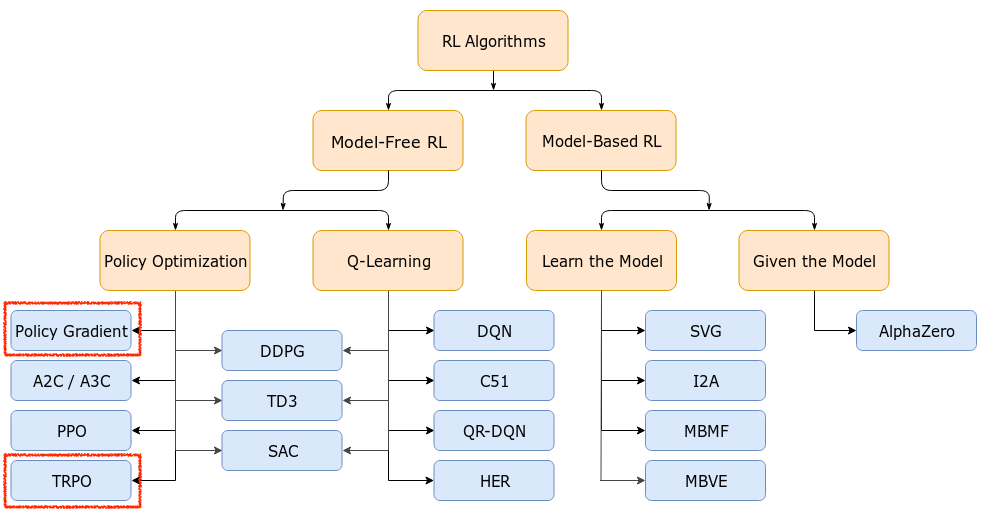 Fig. TRPO가 없어서 OpenAI Taxonomy 추가. OpenAI Spinning Up form OpenAI
Fig. TRPO가 없어서 OpenAI Taxonomy 추가. OpenAI Spinning Up form OpenAI
Reference
- Lectures, Videos, Notes and Talks
- CS285
- CMU 10-703 Deep Reinforcement Learning from Katerina Fragkiadaki
- OpenAI Spinning Up