(RE) A Long Way to Deep Generative Models - Variational AutoEncoders (VAEs)
22 May 2021이번 글에서는 심층 생성 모델 (Deep Generative Models)의 대표적인 application중 하나인 Variational AutoEncoder (VAE)와 이의 다양한 Variations (CVAE, VQ-VAE)에 대해서 알아볼 것입니다.
< 목차 >
- Variational AutoEncoder (VAE)
- What is Generative Model
- What is Latent Variable Model ?
- More Complicated Distribution
- Intractability and revisit Expectation Maximization (EM Algorithm)
- Variational Inference (Variational Approximation)
- Amortized Variational Inference
- Re-Parameterization Trick
- VAE (Full)
- Connection to AutoEncoder (AE)
- VAEs with various type of decoder
- Why does VAE work? (Learned Manifold and Results)
- Various version of VAEs
- Other Deep Genrative Models ?
- References
Variational AutoEncoder (VAE)
Variational AutoEncoder (VAE)는 Kingma라는 연구자에 의해서 2014년에 처음 제안되었습니다.
원 논문은 Kingma, Diederik P., and Max Welling. “Auto-encoding variational bayes.” 으로 사실 이 논문의 내용은 원래도 ML에서 잘 사용되는 Stochastic Variational Inference (SVI) 와 이 Learning Algorithm 을 Large-Scale dataset 에 대해서 어떻게 잘 학습할 것인가? 에 대한 것이고 VAE 는 하나의 Application 에 불과합니다.
(근데 VAE가 너무 유명해서 대부분의 자료에서 상당 부분이 생략되곤 합니다.)
VAE 를 제대로 이해하기 위해서는
- 생성 모델 (Generative Model)이란 무엇인가? (compared to Discriminative Model)
- 잠재 변수 모델 (Latent Variable Model)은 무엇이며 여기서 Latent 는 무슨 의미를 가지고 있을까?
- 어째서 고차원의 잠재 변수 모델은 학습이 어려운가?
- 변분 근사 (Variational Approximation)이란 무엇이고 왜 필요한가? (for intractability)
등에 대해서 알아야 합니다. 그리고 이것들은 Machine Learning (ML)의 핵심적인 개념들이기 때문에 generative model을 하는 사람이 아니더라도 VAE를 한번 공부하고 나면 deep learning 의 기초를 다지는데 굉장히 도움이 됩니다. 이제 차근 차근 generative model이란 무엇인지 VAE 까지 가보도록 합시다.
What is Generative Model
ML은 일반적으로 \(p(x)\)이나 \(p(y \vert x)\)에 대한 분포를 정하고 (gaussian or categorical distribution), 이 distribution 을 나타내는 parameter (gaussian 이면 mean, variance) 내가 가지고 있는 dataset의 distribution 잘 설명하게끔 tuning 하는 것입니다. 이를 likelihood 를 최대화 하는 parameter 를 추정한다 하여 Maximum Likelihood Estimation (MLE)라고 합니다.
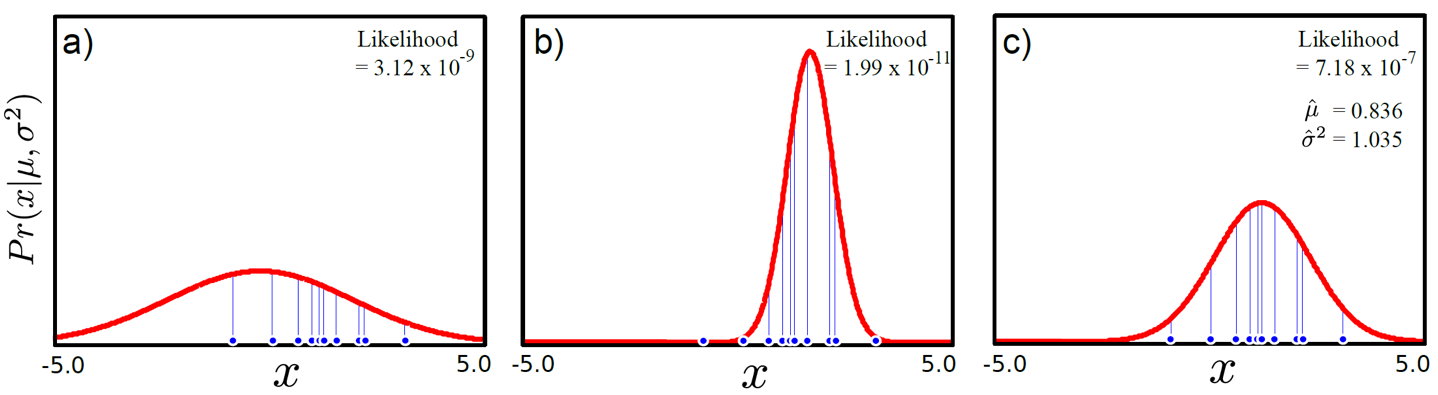 Fig. likelihood를 최대화 한다는 것은 주어진 데이터를 가장 잘 표현하는 분포를 찾는다는 것과 같다.
Fig. likelihood를 최대화 한다는 것은 주어진 데이터를 가장 잘 표현하는 분포를 찾는다는 것과 같다.
여기서 \(p(x \vert y, \theta)\)를 모델링 하는것을 일반적으로 확률적 생성 모델 (Probabilistic Generative Model) 이라고 하며 \(p(y \vert x, \theta)\)를 모델링 하는 것을 확률적 판별 모델 (Probabilistic Discriminative Model)이라고 합니다.
이 둘이 실제로 어떤 차이가 있는지 보기 위해 우리가 어떤 개, 고양이 사진 이미지들을 가지고 이진 분류를 하는 문제를 푼다고 생각해 봅시다. 실제로 이미지는 훨씬 고차원이겠으나 2차원이라고 간단하게 생각해 보겠습니다. Discriminative Modeling 으로 문제를 풀려면 아래의 Log Likelhood 를 최대화 하면 되는데,
\[\hat{\theta} = \arg \max_{\theta} \sum_{n=1}^N \log p(y \vert x, \theta)\]이 때 \(p(y \vert x, \theta)\) 를 Bernoulli distribution 이라고 가정하면 Cross Entropy Loss 를 가지고 최적화 문제를 풀게 되겠습니다.
그렇게 해서 얻게된 \(\theta\) 는 어떤 실제로 아래와 같은 결정 경계면 (decision boundary) 를 나타내는데요,
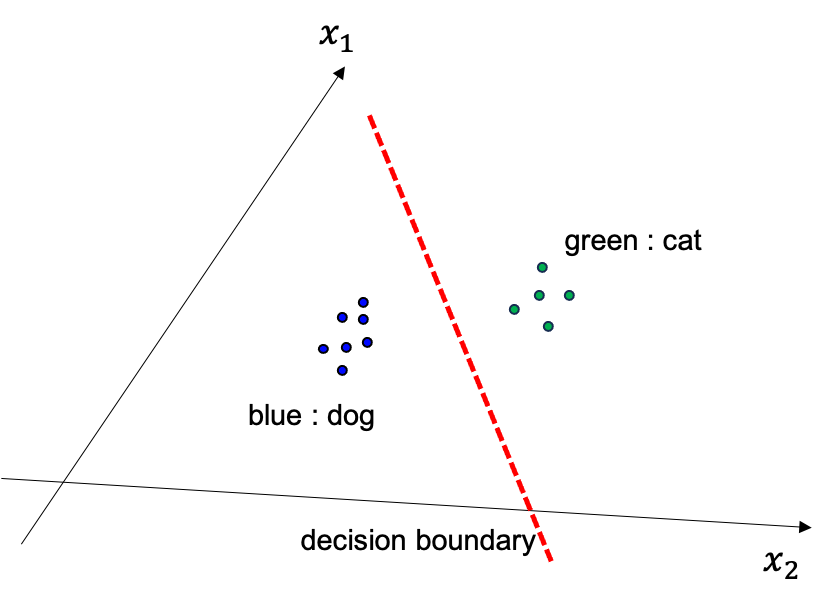 Fig. Discriminative modeling 은 decision boundary 를 찾는 것
Fig. Discriminative modeling 은 decision boundary 를 찾는 것
이는 일반적으로는 cat 일 확률과 dog 일 확률이 0.5 인 중간지점이 됩니다.
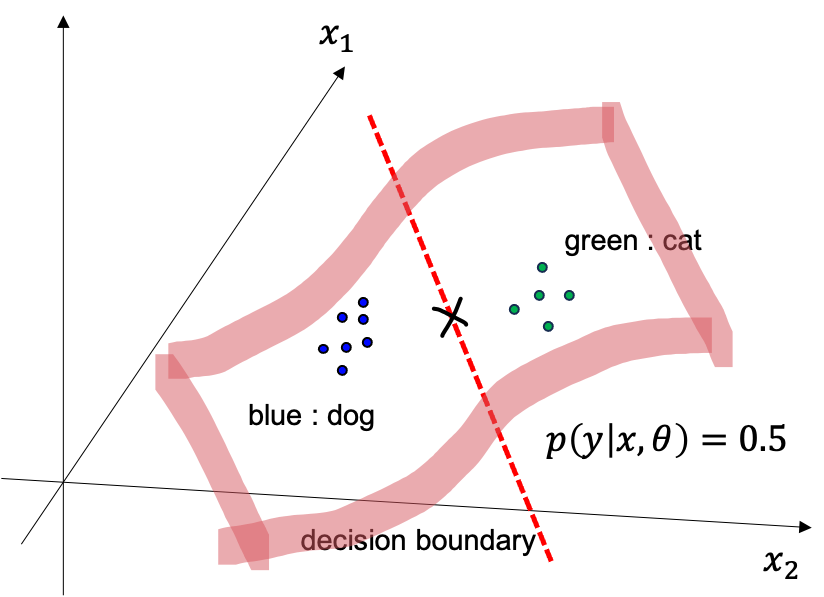 Fig. data 가 2차원일때 decision boundary 를 3차원 에서 본 것
Fig. data 가 2차원일때 decision boundary 를 3차원 에서 본 것
여기에 test data 가 들어오면 경계선을 기준으로 왼쪽이면 개, 오른쪽이면 고양이라고 그냥 하면 되는것이죠.
한편 Generative Modeling 으로도 분류 문제를 풀 수 있는데
\[\hat{\theta} = \arg \max_{\theta} \sum_{n=1}^N \log p(\color{red}{x} \vert y, \theta)\]이 또한 마찬가지로 likleihood를 maximize 하는 parameter 를 찾는 것입니다. 이 때는 일반적으로 \(p(\color{red}{x} \vert y, \theta)\) 를 Gaussian distribution 으로 가정하는데 우리가 실제로 알아내야 하는 것은 class 별로 mean, variance 들을 다 고려해야 하기 때문에 \(\mu_{dog}, \sigma_{dog}, \mu_{cat}, \sigma_{cat}\) 4 개가 됩니다. 마찬가지로 최적화를 통해 문제를 풀면 개에 대한 2차원 Gaussian distribution 과 고양이에 대한 분포를 모두 얻을 수 있게 됩니다.
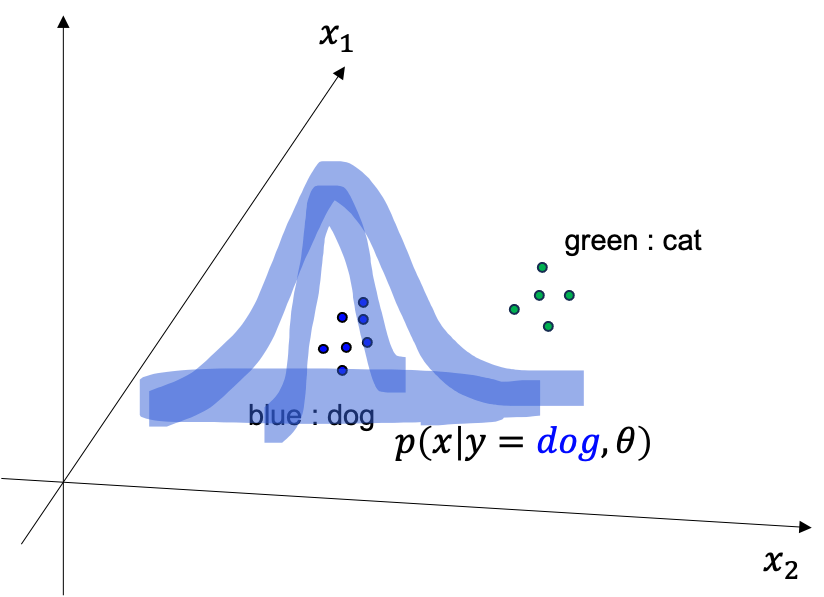 Fig. Conditional Distribution about Dog
Fig. Conditional Distribution about Dog
 Fig. Conditional Distribution about Cat
Fig. Conditional Distribution about Cat
이런경우에는 test data 가 들어오면 두 분포중에서 확률값이 더 큰 class 로 분류를 해주면 되는데
 Fig.
Fig.
이를 따라서 마찬가지로 decision boundary 를 결정할 수 있습니다.
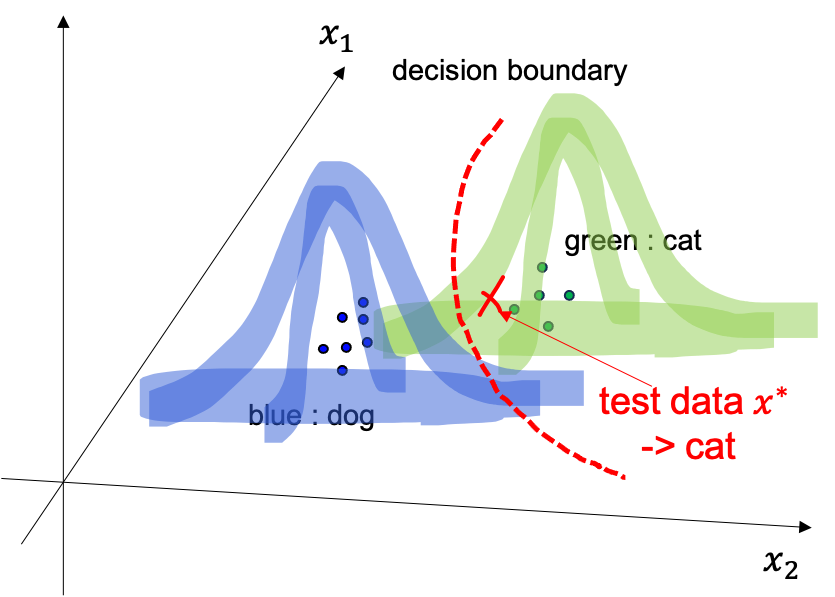 Fig. How can we classify test data?
Fig. How can we classify test data?
그런데 왜 꼭 generative modeling 을 해야할까요? 이게 더 복잡할것 같은데 말이죠.
 Fig. Classification using Generative Model
Fig. Classification using Generative Model
이는 바로 방법론의 이름에 걸맞게 dataset 에는 없지만 새로운 data를 만들어낼 수 있기 때문입니다. 즉 개, 고양이 데이터를 더 만들어낼 수 있는거죠. 왜냐면 우리는 예를 들어 개에 image 분포가 실제로 어떤지를 modeling 했는데 그렇다는 것은 우리가 가지고 있는 image 들이 가장 모여있는 곳을 알고있다는 것이고 (확률이 높은 부근), 그곳에서 2차원 variable 들을 몇개 뽑아보면 실제로 비슷하지만 새로운 이미지를 얻을 수 있기 때문입니다.
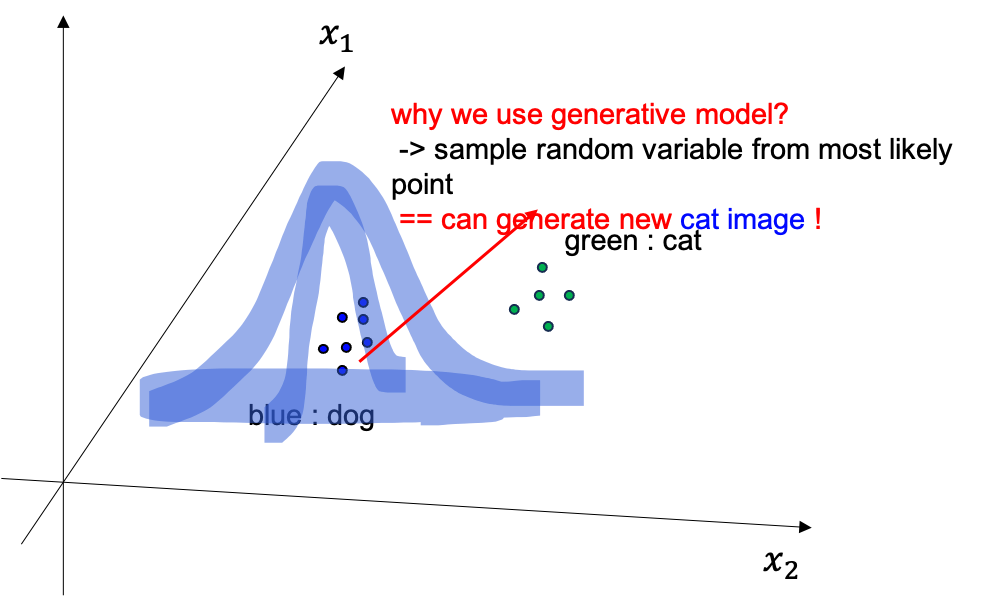 Fig. Generative Model 의 목적
Fig. Generative Model 의 목적
반면 decision boundary 만 달랑 찾는 Discriminative 는 이런일을 할 수가 없는 모델입니다.
What is Latent Variable Model ?
생성모델이 무엇인지는 알겠습니다, 그런데 만약에 label 이 없다면 어떻게 해야할까요?
 Fig.
Fig.
이럴때는 없으면 없는대로 \(p(x \vert \theta)\) likelihood 를 최대화 하면 됩니다. 이것도 생성모델이며 대부분의 생성모델은 사실 x 에 대한 정답 label y 가 없습니다.
 Fig.
Fig.
하지만 아까 개 고양이 이미지들이 두개를 합치면 봉우리가 두개인 (개, 고양이) 복잡한 분포가 될텐데, 이를 아무런 label 정보 없이 하나의 \(p(x \vert \theta) = Norm_x[\mu,\sigma]\) 단봉 gaussian distribution 으로 모델링 하기에는 너무 힘듭니다.
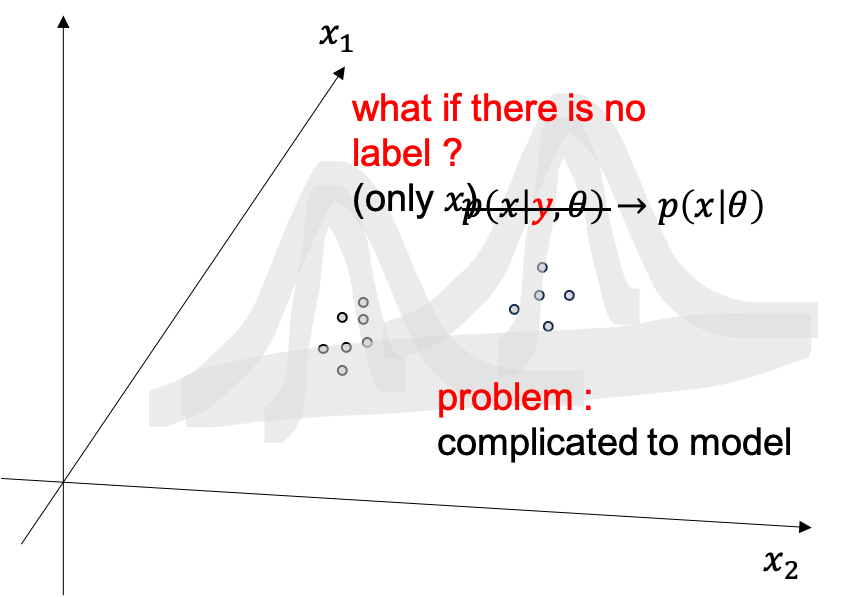 Fig.
Fig.
이럴경우 실제로 주어진 class 정보가 없다 뿐이지, 개 고양이 처럼 비슷한 instance 들을 묶어줄 label이 있을거라고 생각하고 문제를 풀 수있는데,
이 때 이 Fake Label, \(z\) 를 Latent Variable 이라고 합니다.
이 \(z\)는 실제로는 개, 고양이 라는 우리가 생각하는 label이 아닐 수도 있습니다만 어쨌든 이렇게 문제를 풀어 보는 거죠.
 Fig.
Fig.
다시, 잠재 변수 모델 (Latent Variable Model) 은 복잡한 분포를 모델링 하기 위한 방법론으로 원 데이터에는 존재하지 않았던 변수를 데이터 속으로 부터 분리하는 주변화 (Marginalization) 테크닉을 통해 정의하는 것으로 시작합니다.
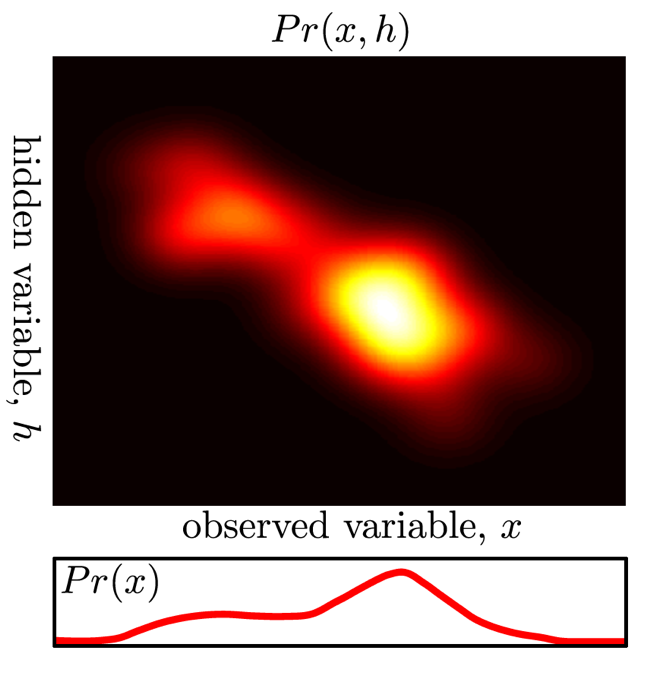 Fig. 잠재 변수 (여기서는 \(h\)라는 notation 으로 쓰임)와 원본 데이터 \(x\)와의 결합 분포, \(h\)의 분포는 그림에서는 연속적인 분포다 (i.e.가우시안)
Fig. 잠재 변수 (여기서는 \(h\)라는 notation 으로 쓰임)와 원본 데이터 \(x\)와의 결합 분포, \(h\)의 분포는 그림에서는 연속적인 분포다 (i.e.가우시안)
만약에 잠재 변수가 이산적인 분포를 갖는 경우를 가정하면 이는 아래와 같은 그림으로 표현할 수 있게 되는데요,
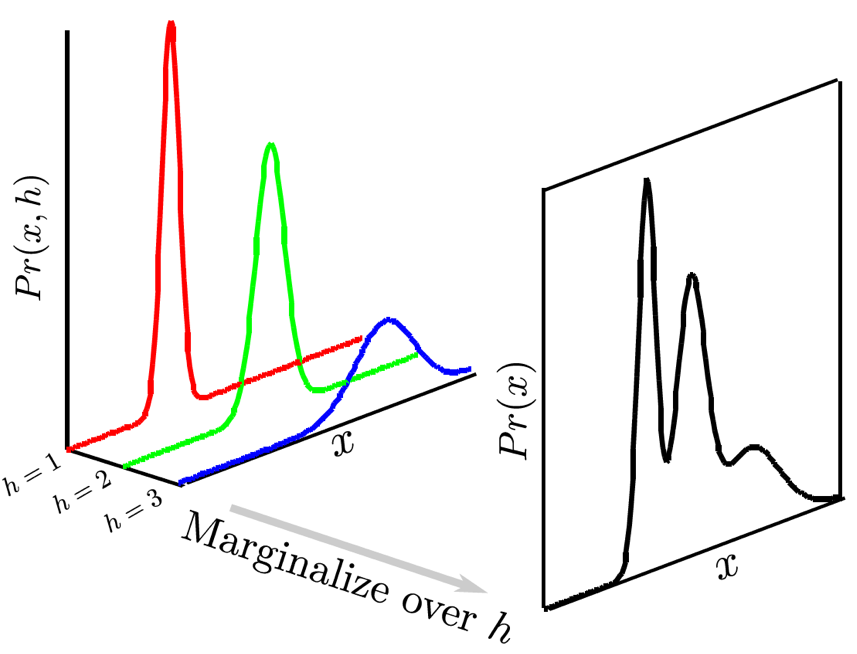 Fig. 만약 잠재 변수 \(h\)의 분포가 이산적인, 예를 들어 3개의 클래스를 가지는 카테고리컬 분포라면, 위의 그림처럼 된다.
Fig. 만약 잠재 변수 \(h\)의 분포가 이산적인, 예를 들어 3개의 클래스를 가지는 카테고리컬 분포라면, 위의 그림처럼 된다.
그림에서 볼 수 있듯, 같은 데이터 포인트 \(x\)라도 \(h=1,2,3\)일 때 각각 리턴하는 확률 값이 다르다는 것을 알 수 있습니다.
(1차원 예시. 각각 개, 고양이, 비행기 image class 라고 생각하면 됨).
이는 각 가우시안 분포 3개를 합치는 것 (Gaussian Mixture Model; GMM) 이라는 method 입니다.
위에서 말씀드린 것 처럼 이는 각 data point 마다 가짜 정답 (Fake Label) 을 달아주고, likelihood 가 높아지도록 학습을 하게되면
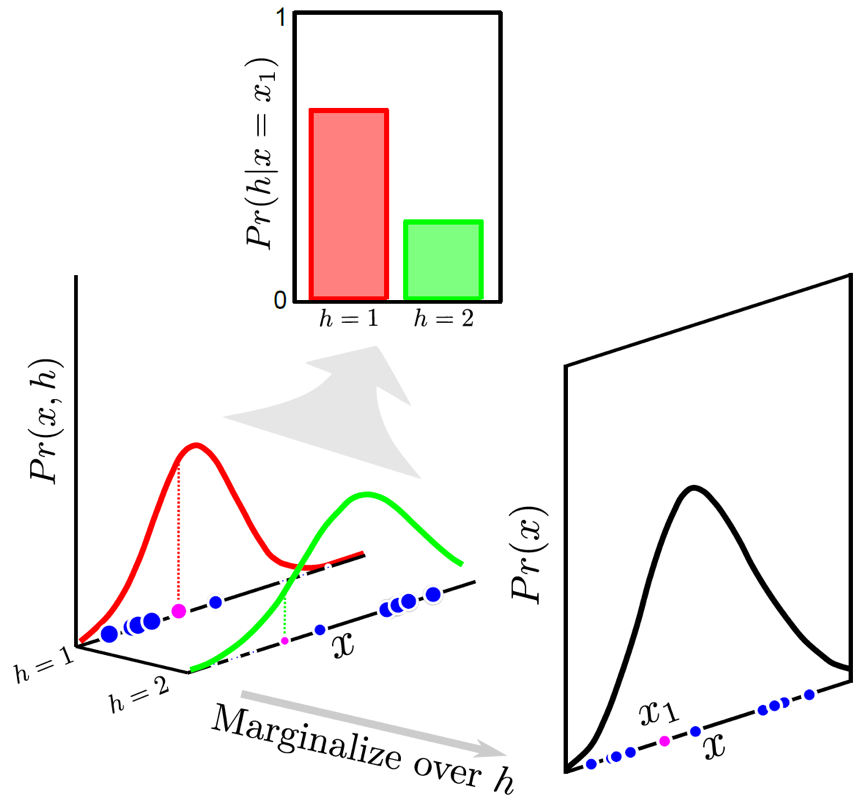
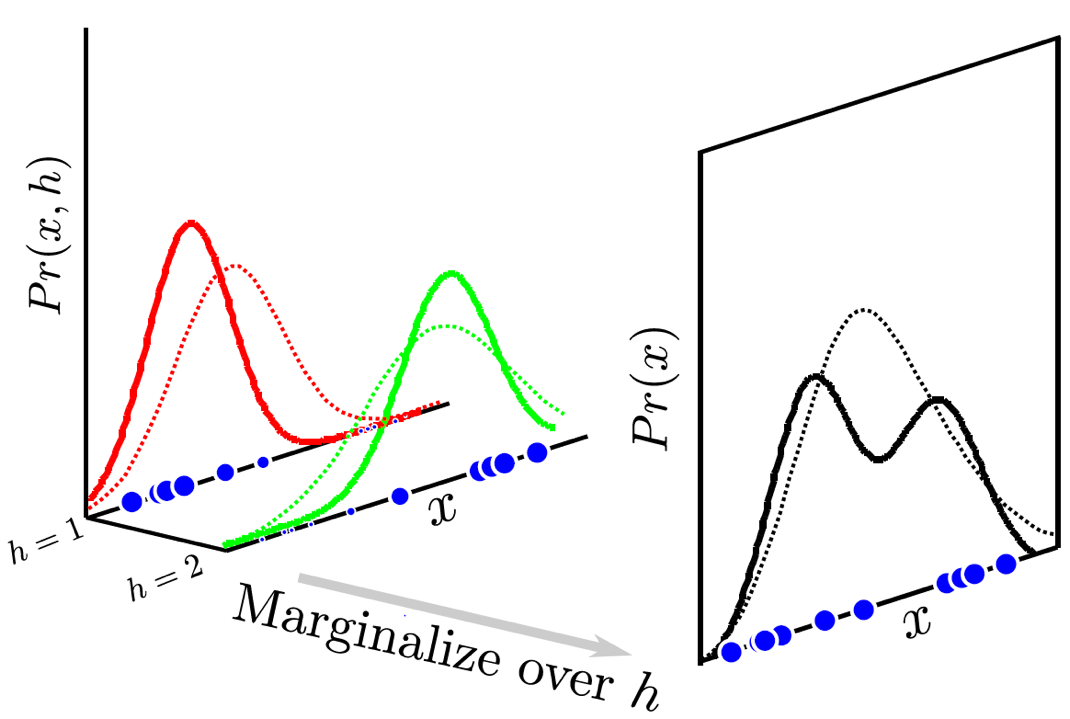 Fig. 학습을 통해 알아서 데이터의 분포를 더욱 잘 설명하는 복잡한 분포를 찾아내는 것을 알 수 있다.
Fig. 학습을 통해 알아서 데이터의 분포를 더욱 잘 설명하는 복잡한 분포를 찾아내는 것을 알 수 있다.
우리가 개, 고양이 label 을 달지 않았음에도 자연스럽게 비슷한 것들끼리는 같은 latent 가 할당되는 것을 볼 수 있습니다.
이러한 잠재 변수 모델은 전통적인 ML 기법인 Expectation Maximization (EM) Algorithm을 통해서 학습하곤 합니다.
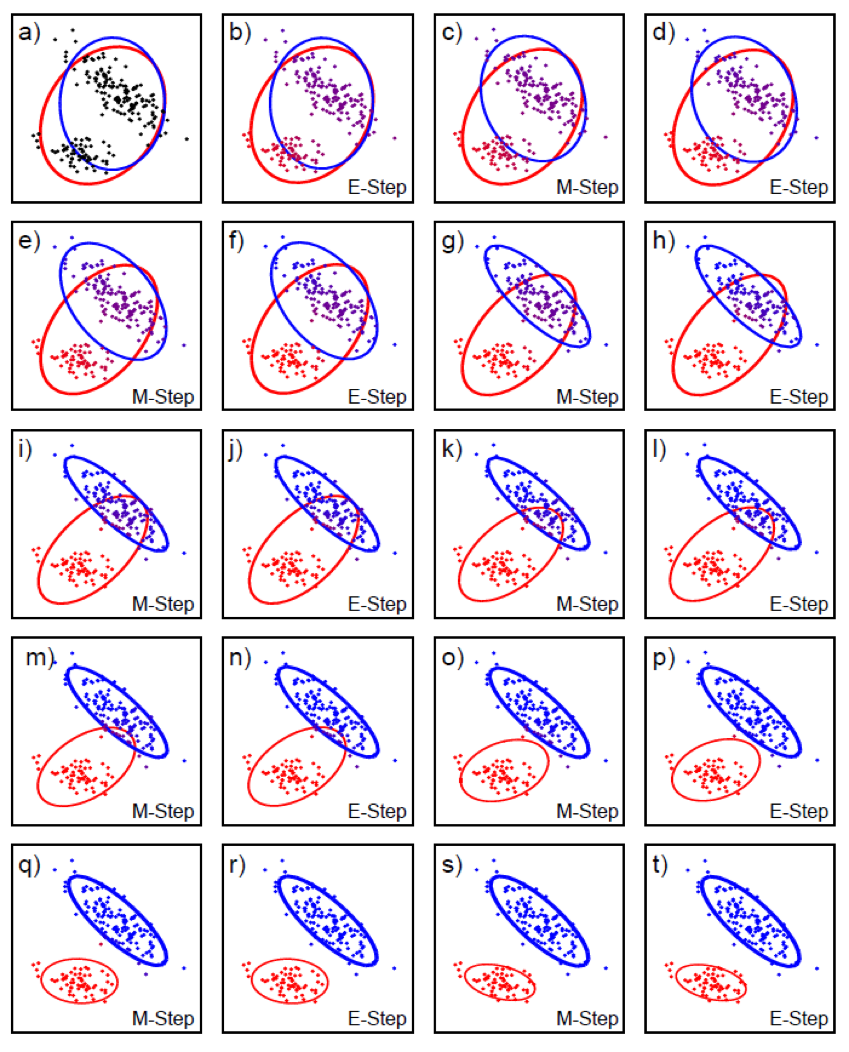 Fig. \(h\)라는 잠재 변수가 어떻게 돼야 한다고 강제한건 아니지만, 학습되는 과정에서 알아서 데이터 분포를 잘 설명하기 위해서 군집끼리 묶는다.
Fig. \(h\)라는 잠재 변수가 어떻게 돼야 한다고 강제한건 아니지만, 학습되는 과정에서 알아서 데이터 분포를 잘 설명하기 위해서 군집끼리 묶는다.
잠재 변수를 표현하기 위해서 원래 우리가 추정하고자 하는 분포 \(p(x)\)를 Marginalization (혹은 integrated out)해서 아래처럼 표현할 수 있다고 말씀드렸었는데 (integral 이냐 summation 이냐는 z 분포가 continuous 냐 discrete 이냐 차이)
\[p(x) \rightarrow p(x) = \sum_z p(x,z)\]이를 아래처럼 더욱 간단하게 표현할 수 있습니다.
\[p(x) = \sum_z p(x \vert z) p(z)\](latent variable 은 판별 모델에도 적용이 될 수 있습니다.)
\[p(y \vert x) \rightarrow p(y \vert x) = \sum_z p(y \vert x,z) p(z)\]이제 이를 조금 더 확장해서 생각해보도록 하겠습니다 (generalization).
More Complicated Distribution
우리가 가지는 데이터에 대한 분포 \(p(x)\)가 연속적이며, 굉장히 복잡한 분포라고 가정해보도록 하겠습니다. 단순히 3개의 gaussian 분포를 합쳐서 (sum) 표현할 정도가 아니라 수십, 수백을 넘어 무한한 분포가 합쳐진 (integral) 굉장히 복잡한 (complicated monstrous) 분포입니다.
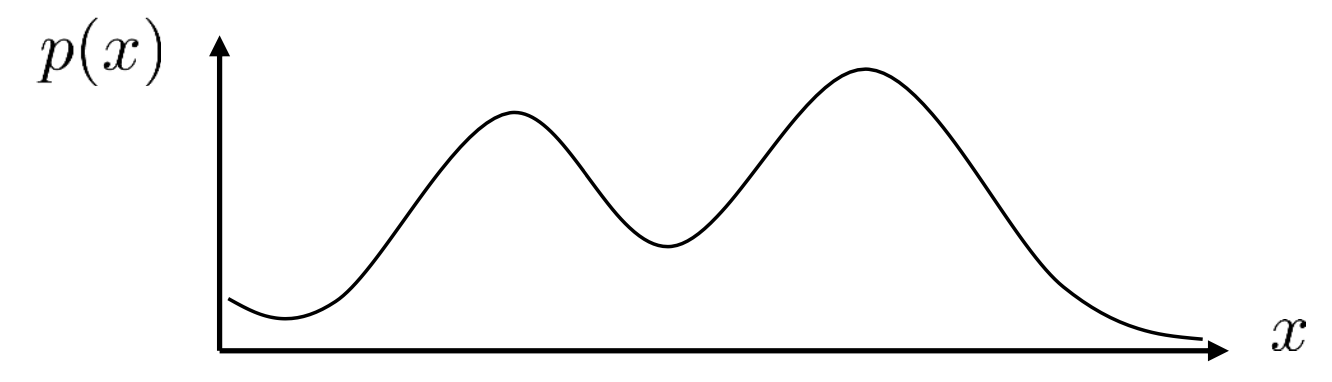 Fig.
Fig.
여기에 위에서 한 것 처럼 잠재 변수를 도입할건데요, 이 때 \(p(z)\)는 매우 다루기 쉬운 연속적인 분포인 gaussian 분포라고 해보도록 하겠습니다.
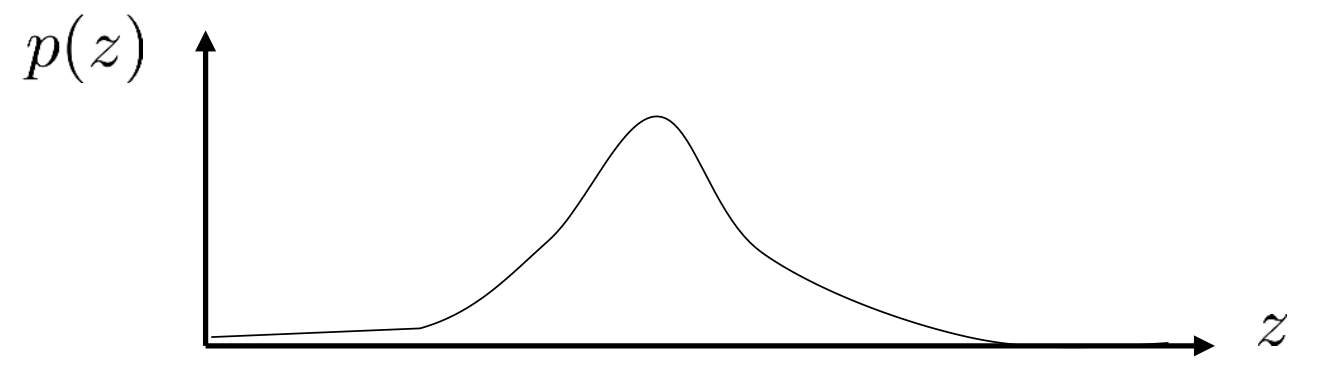 Fig.
Fig.
우리는 z 가 연속적이게 됐으므로 원래 데이터의 분포를 아래처럼 나타낼 수 있습니다.
\[p(x) = \int p(x \vert z) p(z) dz\]우변이 아까와 다르게 \(\sum\)이 아닌 \(\int\)인 이유는 \(p(z)\)가 이번에는 연속적인 분포이기 때문입니다. 즉 z 분포의 가능한 모든 value에 대해 생각을 한다는 겁니다.
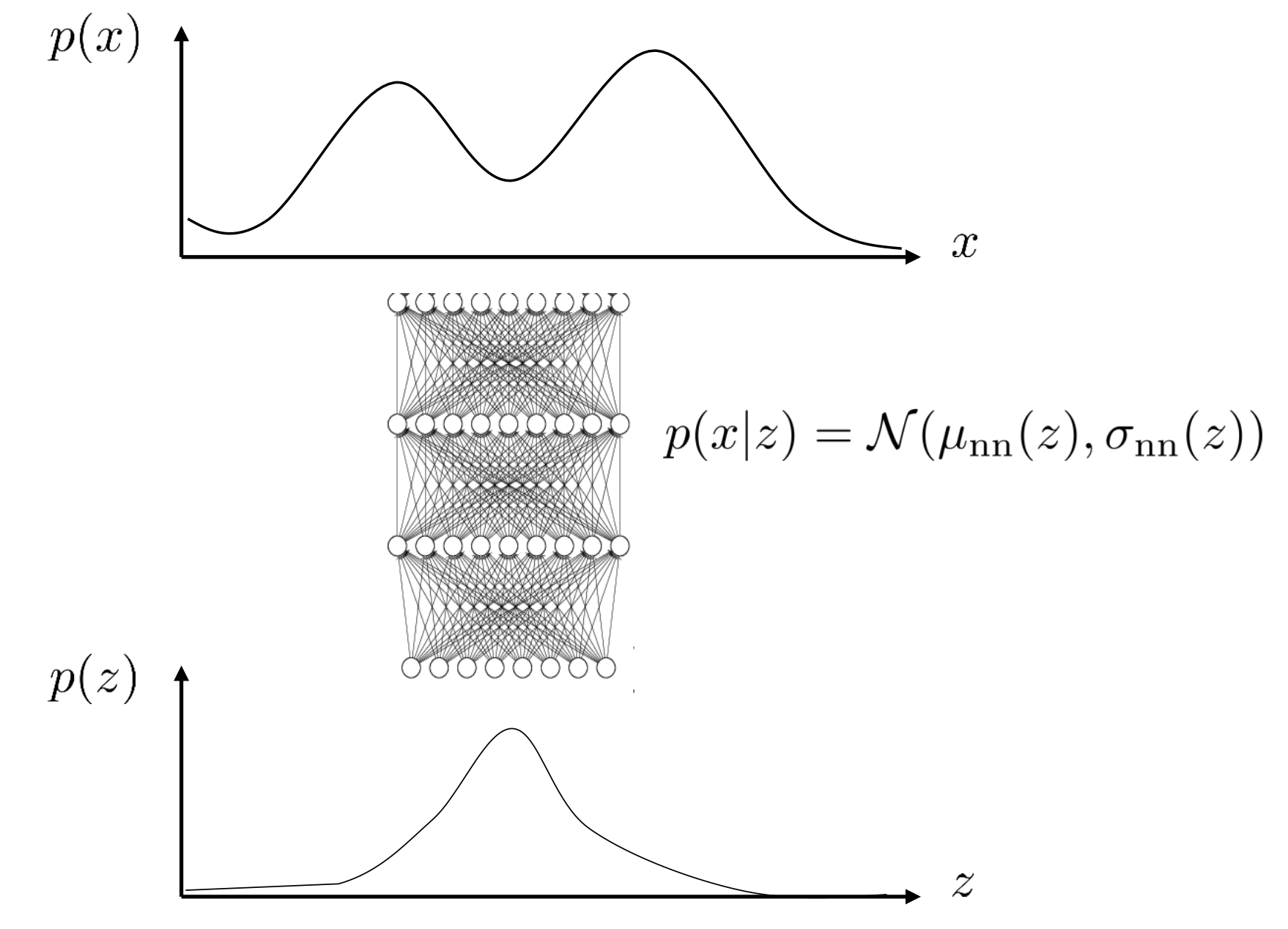 Fig.
Fig.
위의 수식에서 우리가 \(p(z)\) 는 아주 단순한 gaussian 분포임을 알고 있으므로 \(p(x \vert z)\) 만 정의해주면 되는데요, 이 또한 굉장히 다루기 쉬운 가우시안 분포라고 가정 해 보도록 하겠습니다. 우리는 굉장히 복잡한 분포 \(p(x)\)를 매우 간단한 분포인 gaussian 분포 두개의 적분으로 표현하게 되었습니다. 이제 \(p(x \vert z)\) 를 뉴럴네트가 학습하면 되는데요, Log Likelihood 를 Maximize 해야 하는 parameter 를 추정하면 됩니다.
- The model : \(p_{\theta} (x)\)
- The data : \(D = \{ x_1,x_2, \cdots, x_N \}\)
- Maximum likelihood fit : \(\theta \leftarrow argmax_{\theta} \frac{1}{N} \sum_i log p_{\theta} (x_i)\)
우리가 잠재 변수 모델을 정의하기 위해 \(p(x)\)를 Marginalization 했으니 \(p_{\theta}(x)\) 는 다음과 같이 풀어 쓸 수 있습니다.
\[\theta \leftarrow argmax_{\theta} \frac{1}{N} \sum_i log p_{\theta} (x_i) \\ \theta \leftarrow argmax_{\theta} \frac{1}{N} \sum_i log ( \int p_{\theta}(x_i \vert z) p(z) dz ) \\\]그런데 여기서 문제가 있습니다.
적분식이 가지는 의미는 우리가 뭔지 모르는 fake label 의 분포가 연속적인 분포이기 때문에 \(p(z)\)의 가능한 모든 z를 고려하겠다는 것인데, 사실상 이 적분식을 계산하는 것은 불가능에 가깝다고 합니다.
이를 intractable 하다고 합니다.
Intractability 에 대해서는 link 를 보시면 Variational Inference: A Review for Statisticians 라는 reference 를 추천해주는데, 이를 보면 어떤 경우가 Intractable 한지를 조금 더 정확히 알 수 있습니다.
즉 지금의 경우 우리가 먼저 \(p(z), p(x \vert z)\) 를 모두 gaussian 으로 가정했기 때문에 gaussian 끼리의 곱은 gaussian 이어서 계산이 가능해 보여도 차원이 너무 큰 상황에서 전체 z 에 대해 적분하는것이 사실상 계산이 너무 오래걸려 불가능한 케이스 인 것이죠.
 Fig. K차원에 대한 적분은 불가능에 가깝다.
Fig. K차원에 대한 적분은 불가능에 가깝다.
하지만 적분식을 계산할 수 없다고 학습을 할 수 없는건 아닙니다.
모든 변수가 아닌 몇개의 z에대해서만 계산하고 넘어가면 되거든요.
즉 분포 \(p(z)\)에서 가장 그럴듯한 (Likely) \(z\) 값을 sampling 해서 이거만 쓰는걸로 적분을 근사해버리면 됩니다.
이렇게 몇개씩 sampling 하는걸로 대체하는걸 Expected log-likelihood 라고 하거나 Monte Calro 방법을 쓴다고 얘기합니다.
각 data point \(x_i\)마다 1개 혹은 몇개의 뽑힌 \(z\)에 대해서만 liklihood를 계산하기 때문에 때문에 부담이 확 줄어들었습니다. 여기서 \(p(z) = N(0, I)\) 는 zero mean unit variance 인 단순 prior 라 parameter 가 없고 \(p_{\theta} (x_i \vert z)\)는 gaussian likelihood 이므로 MSE loss 로 학습을 하면 됩니다.
Intractability and revisit Expectation Maximization (EM Algorithm)
WARNING !!! Missing Link
data point, \(x_i\) (i.e. 이미지)마다 어떤 \(z\)가 동반되어야 하는지? (어떤 \(p(z \vert x_i)\) 를 가지는지) 추론 (infer) 하는것이 필요한데, 그렇기 때문에 이 학습 과정을 확률적 추론 (Probabilistic Inference)이라고 부르기도 합니다.
즉, 우리가 정말로 원하는 것은 \(p(z)\)로 부터 샘플링한 벡터를 이용해서 새로운 \(x_i' \approx x_i\)를 만드는, \(p(x_i \vert z)\)라는 mapping function을 학습하는 것이지만,
 Fig. \(p(x \vert z)\)
Fig. \(p(x \vert z)\)
이를 위해서 역으로 \(p(z \vert x_i)\) 라는 주어진 입력으로 부터 주어지는 \(z\)는 과연 어떤 분포일까?를 나타내는 \(p(z \vert x_i)\)까지도 추론해야 한다는 거죠.
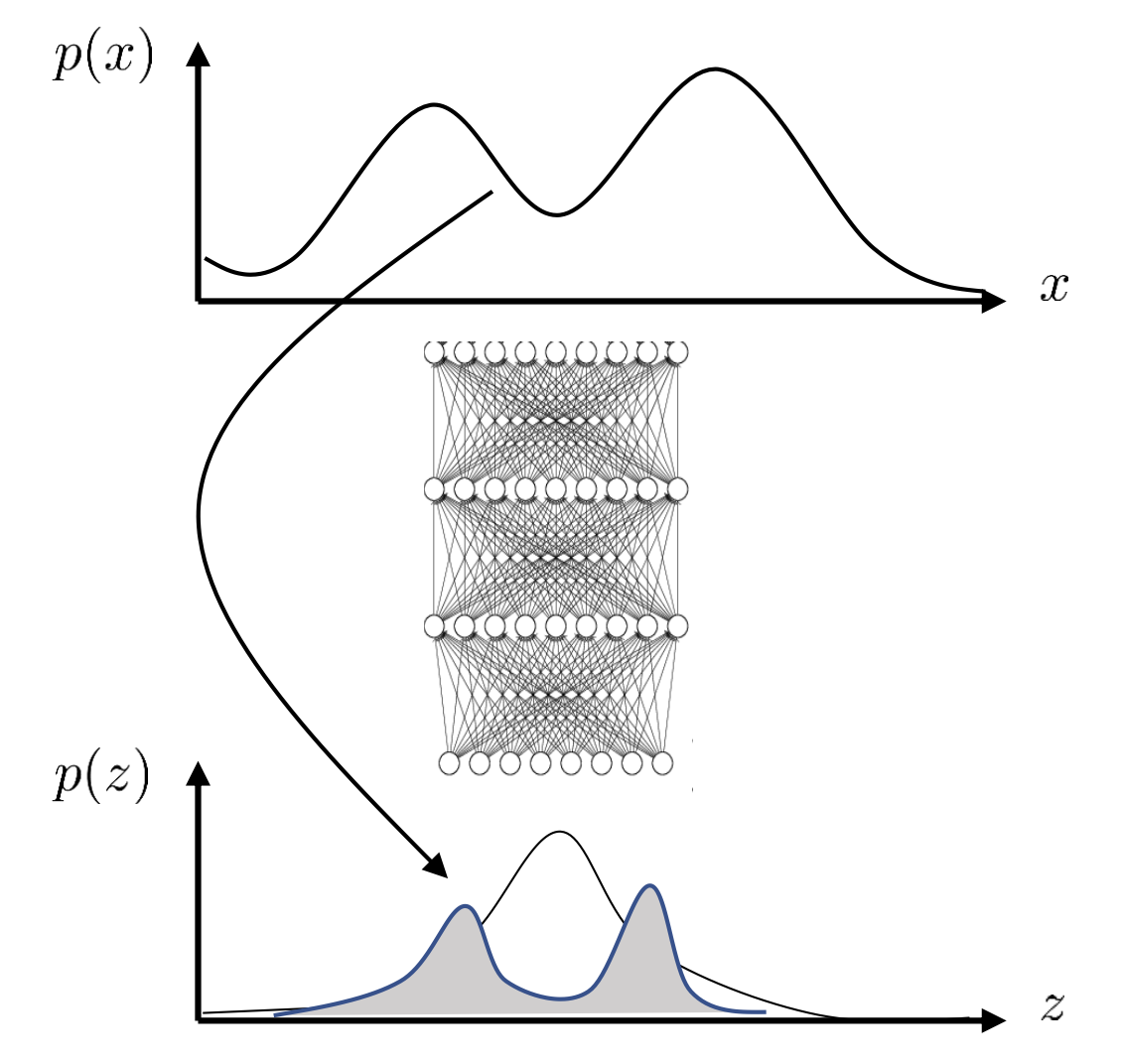 Fig. \(p(z \vert x)\)
Fig. \(p(z \vert x)\)
하지만 이 분포가 어떻게, 얼마나 복잡하게 생겼는지 모른다는게 또 골치인데요, 그렇기 때문에 우리는 근사 추론 (approximate inference) 방법을 사용해서 학습을 하게 되고,
이 때 자주 쓰이는 방법이 바로 변분 추론 (variational Inference)혹은 변분 근사 (variational approximation) 라는 방법이 됩니다. (VAE 의 V)
Variational Inference (Variational Approximation)
변분 추론의 핵심 아이디어는 계산하기 복잡한 \(p(z \vert x)\) 대신에, 이와 유사하지만 간단한 분포 (i.e. 가우시안 분포)를 사용하자는 겁니다.
\[p(z \vert x_i) \rightarrow q_i(z) = N(\mu_i, \sigma_i)\]수식에서도 알 수 있듯이, 이는 각각의 학습 데이터셋의 데이터 포인트인 \(x_i\)마다 서로 다른 \(\mu_i,\sigma_i\)를 가지고 있을 겁니다.
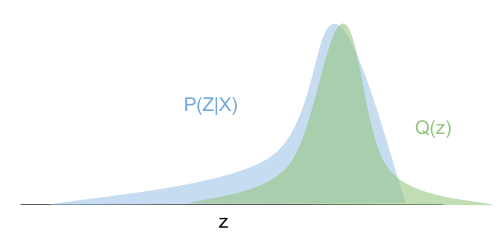 Fig. Variational Approximation
Fig. Variational Approximation
여기서 \(p(z \vert x_i)\)를 진짜 사후 분포 (real posterior distribution) 라고 표현합니다.
이는 단순한 가우시안 분포가 아니라 굉장히 복잡하게 생겨 모델링 하기도 힘들며, 실제로 우리가 알지 못하는 분포입니다.
- real data distribution : \(p(x_i)\)
- real posterior : \(p(z \vert x_i)\)
- prior : \(p(z)\)
- approximate posterior : \(q_i(z)\)
여기서 어떤 \(q_i(z)\)를 설정하던지, 우리는 \(logp(x_i)\)에 대한 하계 (Lower Bound)를 설정할 수가 있는데요,
이는 아래의 수식을 통해서 정의할 수 있습니다.
위에서 사용된 테크닉은 \(\frac{q_i(z)}{q_i(z)} = 1\)을 추가하고, 기대값의 정의를 사용한 것 밖에 없습니다.
여기서 추가적으로 변분 추론의 핵심인 Jansen's Inequality 라는 아래의 특성을 사용하고
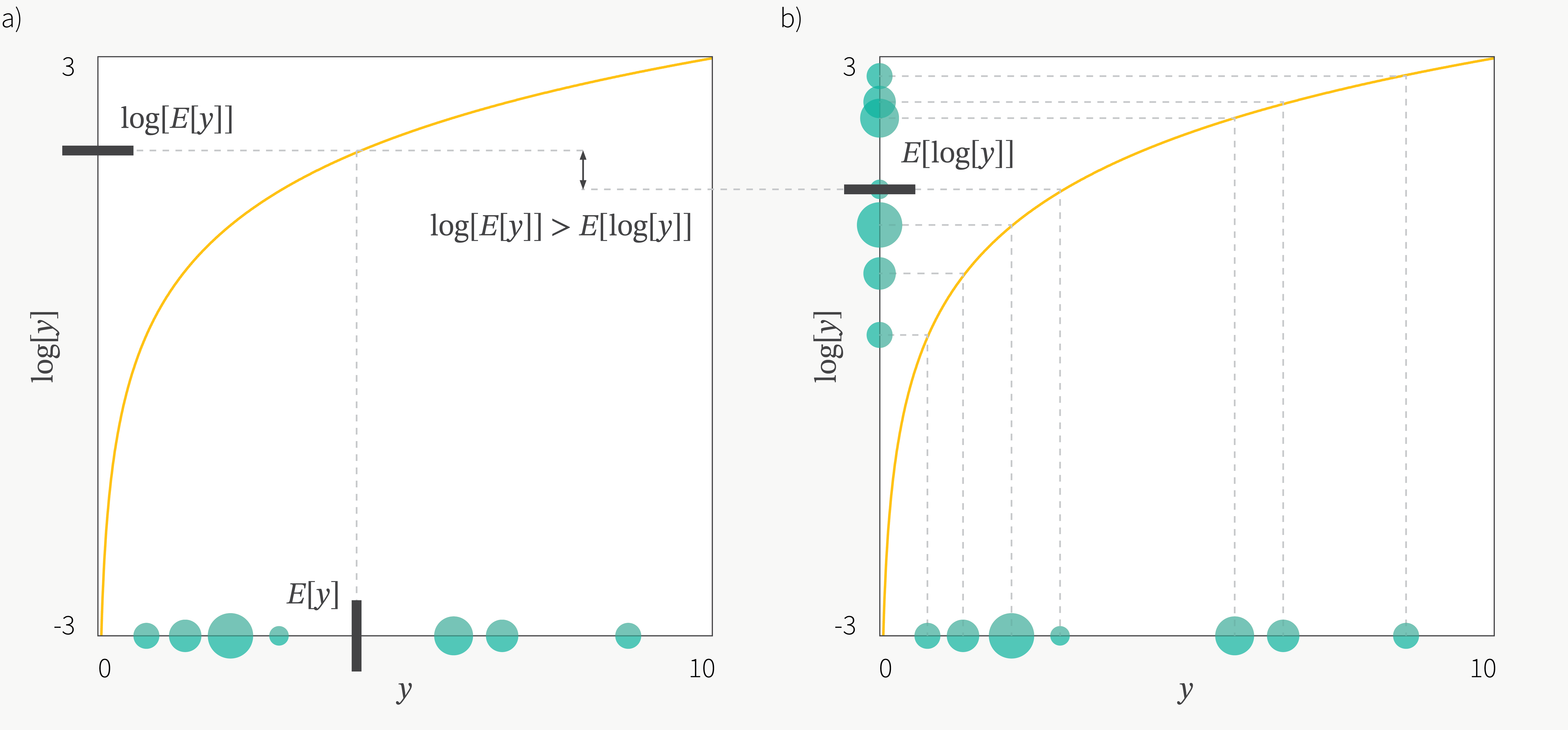 Fig. Jensen’s Inequality
Fig. Jensen’s Inequality
Jansen’s Inequality 를 사용해 얻은 부등식의 log 가 취해진 항을 적당히 분리할 수 있는데요,
\[\begin{aligned} & \log p(x_i) = \log \mathbb{E}_{z \sim q_i(z)} [ \frac{p(x_i \vert z) p(z) }{q_i(z)} ] & \\ & \geq \mathbb{E}_{z \sim q_i(z)} [ \log \frac{p(x_i \vert z) p(z) }{q_i(z)} ] = \mathbb{E}_{z \sim q_i(z)} [\log p(x_i \vert z) + \log p(z)] - \mathbb{E}_{z \sim q_i(z)} [\log q_i(z)] & \end{aligned}\]생성 모델 이란 결국 모든 데이터 포인트들에 대한 log-likelihood, \(\log p(x_i)\)의 합인 \(log p(x) = \sum_i \log p(x_i)\)를 최대화 하는 문제인데, \(\mathbb{E}_{z \sim q_i(z)} [\log p(x_i \vert z) + \log p(z)] - \mathbb{E}_{z \sim q_i(z)} [\log q_i(z)]\) 라는 term이 Lower Bound이기 때문에 이를 최대화 하는 것이 곧 \(log p(x)\) 를 최대화 하는 문제를 푸는 것과 다름 없다는 사실을 알 수 있게 됩니다.
Entropy
다시 돌아와서, 우리가 최대화 하고자 하는 Lower Bound 수식의 두번째 term은 사실 음의 엔트로피 (negative Entropy)와 동일한 수식임을 알 수 있습니다.
그렇기 때문에 우리는 수식이 갖는 의미를 좀 더 해석해 볼 수 있는데, 이를 위해 먼저 엔트로피 (Entropy)에 대해 알아야 합니다.
엔트로피가 의미하는 바는 직관적으로 다음과 같습니다.
- 얼마나 확률 분포가 랜덤한가? (how random is the random variable?)
- 주어진 확률 분포 하에서 log 확률값에 대한 기대값이 얼마나 큰가? (how large is the log probability in expectation under itself?)
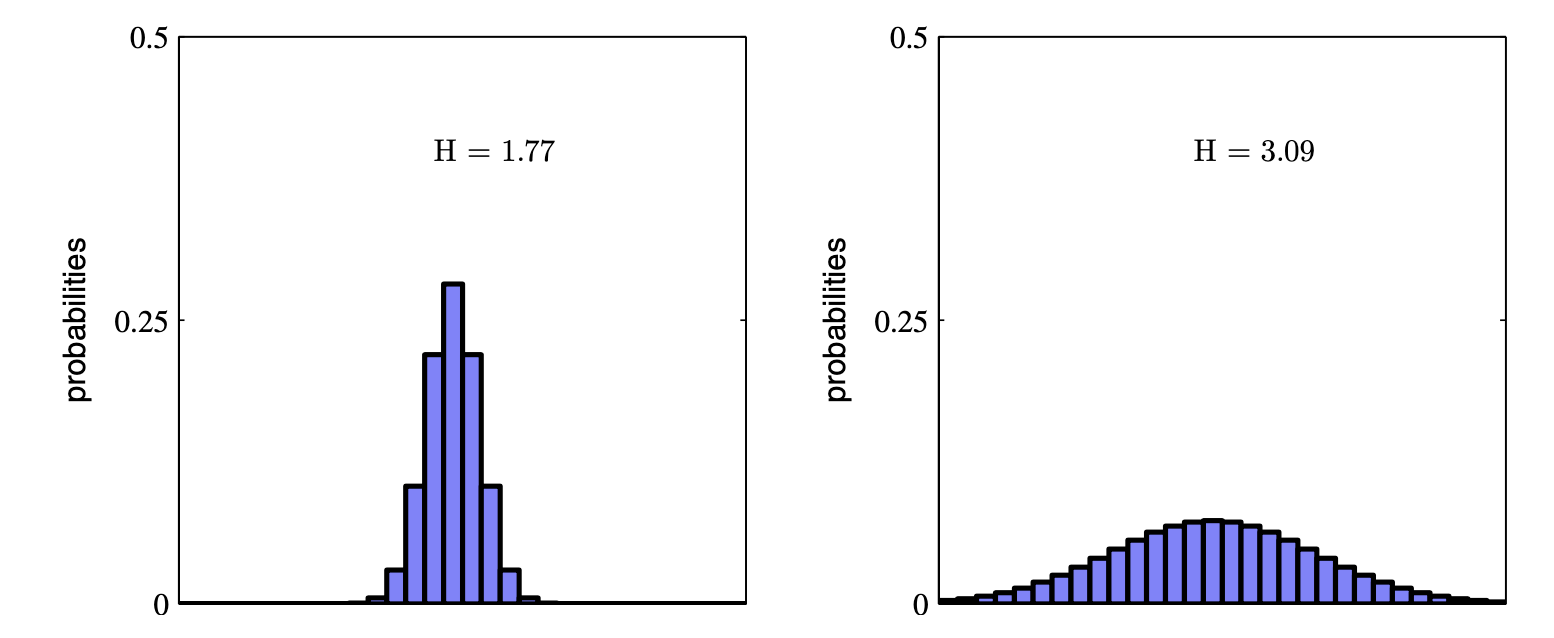 Fig. 더욱 랜덤한 오른쪽 분포가 더 엔트로피가 높다.
Fig. 더욱 랜덤한 오른쪽 분포가 더 엔트로피가 높다.
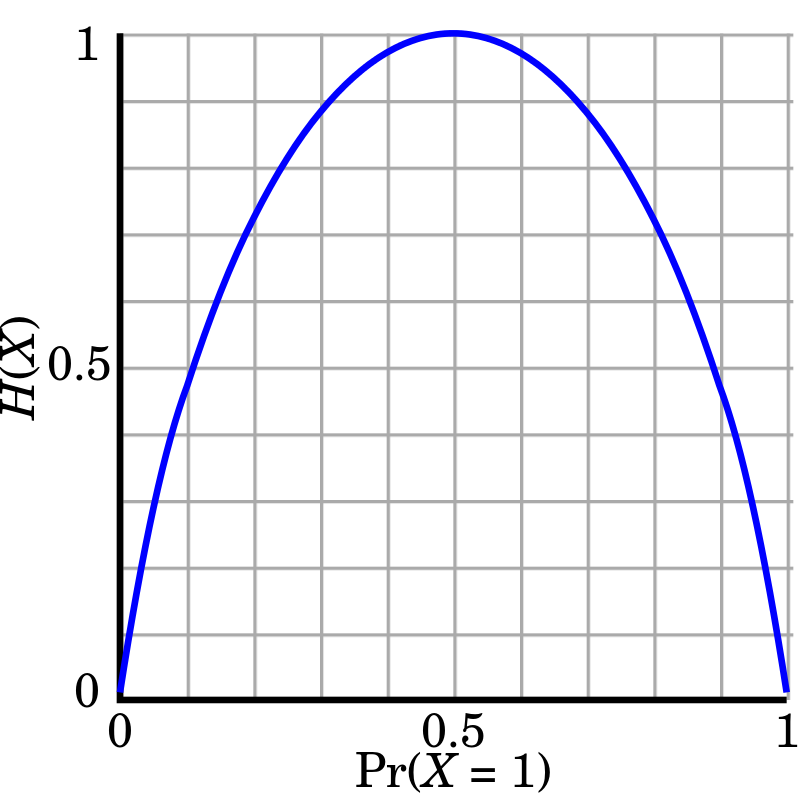 Fig. 베르누이 분포 하에서의 Entropy, 나올 수 있는 경우 2가지가 모두 0.5일 때, 가장 헷갈리는 상황으로 엔트로피가 가장 높다.
Fig. 베르누이 분포 하에서의 Entropy, 나올 수 있는 경우 2가지가 모두 0.5일 때, 가장 헷갈리는 상황으로 엔트로피가 가장 높다.
즉 엔트로피는 얼마나 확률 분포가 랜덤한가? 인데, 우리가 최대화 하려고 하는 수식이 바로 \(q_i(z)\) 의 엔트로피를 포함하고 있기 때문에, 아래의 수식을 최대화 하는 것은
\[\mathbb{E}_{z \sim q_i(z)} [log p(x_i \vert z) + log p(z)] + H(q_i)\]바로 \(q_i(z)\) 분포를 평평하게 (랜덤하게) 만들면서, 이로부터 샘플링한 z라는 랜덤 변수 (random variable)을 가지고 만들어낸 이미지가 \(log p(x_i \vert z)\) 원본 이미지 \(x_i\)가 되게끔 하는 것을 의미하게 된다는 겁니다.
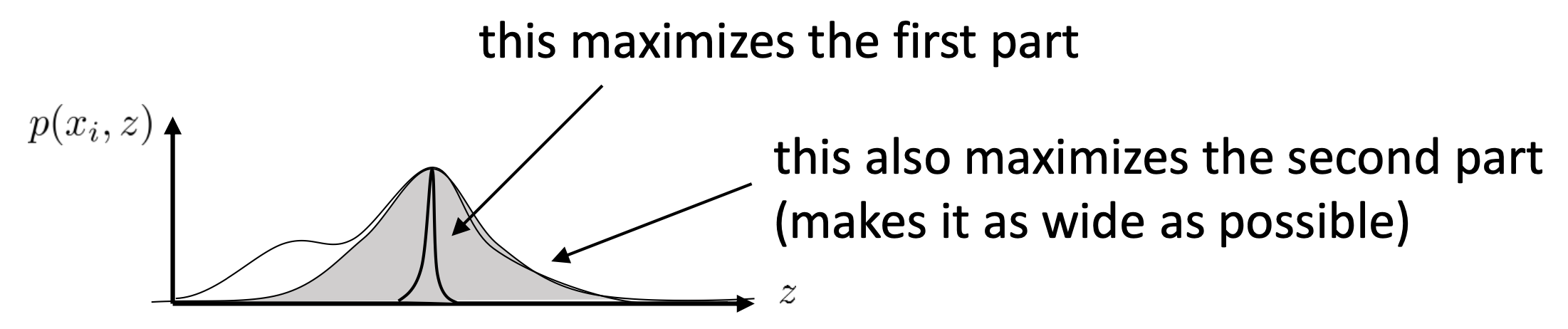 Fig. 우리가 최대화 하려는 수식의 첫 번째 term과 두 번째 term이 가지는 의미
Fig. 우리가 최대화 하려는 수식의 첫 번째 term과 두 번째 term이 가지는 의미
KL-Divergence (KLD)
이 수식을 해석하는 또 다른 방법은 바로 쿨백 라이블러 발산 (KL-Divergence, KLD)을 이용하는 건데요,
KLD는 서로 다른 두 분포에 대해서 다음의 수식을 만족합니다.
간단하게 KLD는 '두 분포가 얼마나 다른가' 혹은 '두 분포간의 거리'를 의미하며, 수식의 결과값이 작을수록 두 분포가 유사하다는 뜻을 나타냅니다.
즉 두 분포가 완전히 같다면 이 값은 \(0\)이 됩니다. (\(0\)이 되는지는 수식의 기대값에 같은 분포를 넣어서 계산하면 쉽게 확인할 수 있습니다.)
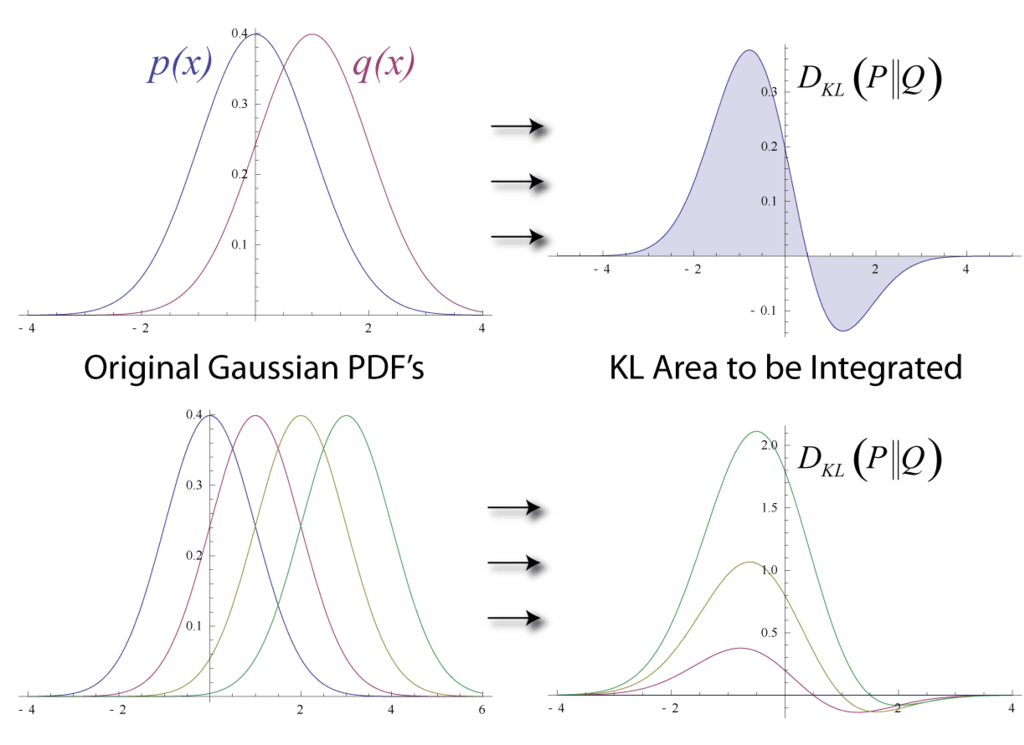 Fig. Wikipedia에 묘사되어 있는 KLD.
Fig. Wikipedia에 묘사되어 있는 KLD.
KLD 에서의 거리라는 개념은 널리 알려져 있는 것처럼 흔히 말하는 좌표상의 유클리디안 거리 (Euclidean Distance)가 아니며, \(D_{KL}(p \parallel q)\)와 \(D_{KL}(q \parallel p)\)의 결과값은 서로 같지 않습니다. 그리고 KLD의 특성중 하나는 리턴하는 값이 언제나 양수라는 특징을 가지고 있습니다.
어쨌든 KLD를 갑자기 설명한 이유가 있는데,
그건 바로 우리가 Jensen’s Inequality로 유도한 수식이 KLD 와 관련이 있기 때문입니다.
우리가 posterior 를 \(q\)로 근사하려고 하는데 그럼 “어떤 \(q_i(z)\)가 좋은 근사 분포일까”요?
이는 유도했던 수식의 bound가 '얼마나 tight한가'? 다시 풀어서 말하면, '얼마나 우변과 좌변이 유사한가?'를 재보면 알 수 있습니다.
근사 분포 \(q_i(z)\)는 \(p(z \vert x_i)\) 와 유사하지만 다루기가 쉬운 분포여야 하며, 이를 잘 반영했을 때가 좌변과 우변이 차이가 가장 적어지고, 그랬을 때 \(q\)가 좋은 \(q\)가 된다는 겁니다.
KLD로 \(q_i(z)\)는 \(p(z \vert x_i)\) 이 차이를 measure 해 봅시다.
우리는 위와 같은 수식을 얻을 수 있고, 이 수식을 아래와 같이 잘 전개하면 재밌는 결과를 얻을 수 있습니다.
\[\begin{aligned} & \color{green}{D_{KL} (q_i(z) \parallel p(z \vert x_i))} = \mathbb{E}_{z \sim q_i(z)} [log \frac{q_i(z)}{p(z \vert x_i)}] & \\ & = \mathbb{E}_{z \sim q_i(z)} [log \frac{ q_i(z) p(x_i) }{ p(x_i,z) }] & \\ & = -\mathbb{E}_{z \sim q_i(z)} [log p(x_i \vert z) + log p(z)] + \mathbb{E}_{z \sim q_i(z)} [log q_i(z)] + \mathbb{E}_{z \sim q_i(z)} [log p(x_i)] & \\ & = - \mathbb{E}_{z \sim q_i(z)} [log p(x_i \vert z) + log p(z)] - H(q_i) + log p(x_i) & \\ & = - \color{blue}{L_i (p,q_i)} + \color{red}{log p(x_i)} & \end{aligned}\]바로 \(log p(x_i)\)가 아까 정의한 Lower Bound인 \(L_i(p,q_i)\)와 \(D_{KL} (q_i(z) \parallel p(z \vert x_i))\)의 합이라는 겁니다.
- log p(x)를 일반적으로
증거 값 (Log Evidence)이라고 부르는데요, 이 값은 정확하게 \(L_i\)와 KLD값의 합이며 이 KLD는 언제나 양수값이기 때문에 \(L_i\)는 언제나 Evidence보다 조금 아래에 놓이게 되는 하계 (Lower Bound)가 됩니다. 그렇기 때문에 일반적으로 \(L_i(p,q_i)\)를Evidence Lower Bound (ELBO)라고 합니다.
여기서 햇갈리실 수도 있는데 \(p(x) = \int_{\theta} p_{\theta}(x) d \theta\), Evidence 와 \(p_{\theta}(x)\), Likelihood 는 다른 겁니다. Likelihood 를 다 파라메터 공간 상에서 적분해야 Evidence = Marginal Likelihood가 됩니다.
이 수식이 시사하는 바는 다음과 같습니다.
\[log p(x_i) = D_{KL} (q_i(z) \parallel p(z \vert x_i)) + L_i (p,q_i)\]바로 이는 \(L_i(p,q_i)\)를 유도하는 또 다른 방법이기도 하며 \(log p(x_i)\)와 ELBO \(L_i\)간의 괴리 (error)가 얼마나 크고 작은지를 알 수 있기 때문입니다.
만약 두 진짜 분포와 근사 분포간의 KLD가 작다고 생각하면, \(L_i\)가 \(log p(x_i)\)를 굉장히 잘 근사 (bound가 굉장히 tight해짐) 한다는 걸 알수 있겠죠? (극단적으로 0이면, 둘은 동일함) 이러한 특성은 매우 매우 중요한 특성인데요, 만일 우리가 KLD를 최소화 하면서, 동시에 \(L_i\)를 최대화 하면 우리는 정말 효과적으로 \(p(x_i)\)를 극대화 할 수 있을겁니다.
\[\begin{aligned} & log p(x_i) = D_{KL} (q_i(z) \parallel p(z \vert x_i)) + L_i (p,q_i) & \\ & log p(x_i) \geq L_i(p,q_i) & \end{aligned}\]그리고 우리는 KLD가 언제나 양수이며, KLD와 \(L_i\)의 합이 \(logp(x)\)라는 사실로 부터, 즉 우리는 \(L_i\)를 \(q_i\)에 대해서 최대화 하는 것이 즉 KLD를 최소화 한다는걸 알 수 있습니다.
\[\begin{aligned} & D_{KL} (q_i(z) \parallel p(z \vert x_i)) = - \mathbb{E}_{z \sim q_i(z)} [log p(x_i \vert z) + log p(z)] - H(q_i) + log p(x_i) & \\ & = - L_i (p, q_i) + log p(x_i) & \end{aligned}\](여기서 \(logp(x_i)\) 는 \(q_i\)와 관련이 없기 때문에 (독립) 고정되어있음)
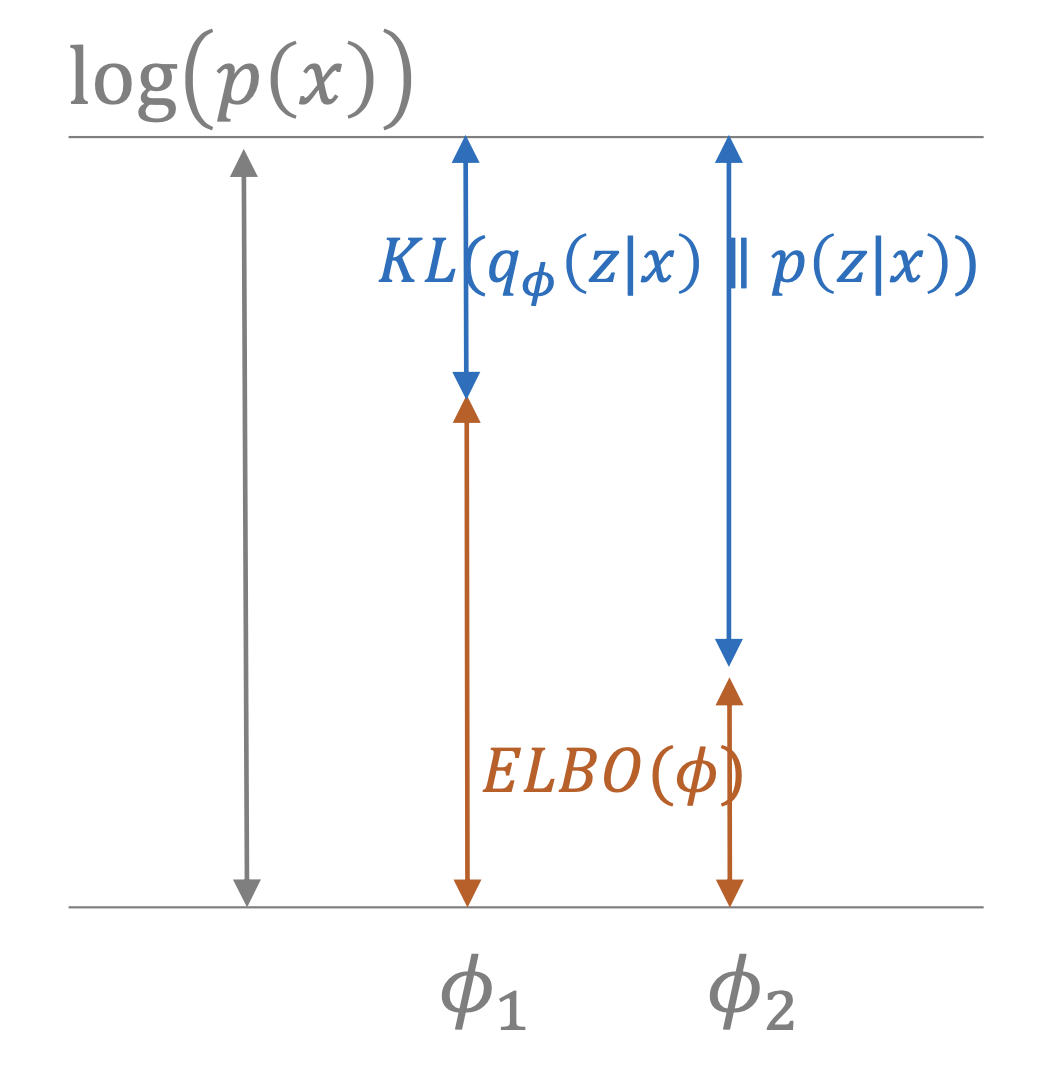 Fig. \(L_i\)를 최대화 하는 것은, 실제 분포와 근사 분포의 KLD를 최소화 하는 것이다. (Notation이 다른 이유는 후에 다시 서술하도록 하겠습니다.)
Fig. \(L_i\)를 최대화 하는 것은, 실제 분포와 근사 분포의 KLD를 최소화 하는 것이다. (Notation이 다른 이유는 후에 다시 서술하도록 하겠습니다.)
결론적으로 우리는 ELBO를 \(p\)와 \(q\) 모두에 대해서 최대화 하는 것이 결국 생성 모델이 원하는 진짜 목적 함수 (Objective Function), \(log p(x)\)를 최대화 하게 되는 겁니다.
- ELBO를 \(q\)에 대해서 최대화 : \(p,q\) 사이의 KLD가 줄어든다 -
bound가 tight해진다 - ELBO를 \(p\)에 대해서 최대화 : \(log p(x_i) \geq L_i\)의 \(L_i\)이 커지면서 \(log p(x_i)\), 즉
Likelihood 도 덩달아 커진다.
이렇게 우리는 잠재 변수 모델 (Latent Variable Model)을 학습할 수 있는 tractable한 방법을 얻게 되었습니다.
즉, 이제 우리는 아래의 수식이 아니라
\[\theta \leftarrow arg max_{\theta} \frac{1}{N} \sum_i log p_{\theta} (x_i)\]ELBO를 최대화 함으로써 생성 모델을 학습할 수 있게 된겁니다.
조금 더 디테일하게는 아래의 학습 절차 (training procedure) 따르면 되겠습니다.
\[\begin{aligned} & \text{for each } x_i (\text{or mini-batch}): & \scriptstyle{\text{; for every data } x_i { in our dataset}} \\ & \quad \text{calculate } \bigtriangledown_{\theta} L_i(p,q_i): & \scriptstyle{\text{; calculate gradient of ELBO with respect to model param}} \\ & \quad \quad \text{sample } z \sim q_i(z) & \scriptstyle{\text{; 1. sample z because we have Expectation}} \\ & \quad \quad \bigtriangledown_{\theta} L_i(p,q_i) \approx \bigtriangledown_{\theta} log p_{\theta} (x_i \vert z) & \scriptstyle{\text{; 2. calculate gradient for one sample (can use multiple sample). p(z) has no parameter}} \\ & \quad \theta \leftarrow \theta + \alpha \bigtriangledown_{\theta} L_i(p,q_i) & \scriptstyle{\text{; 3. update param on } \theta} \\ & \quad \text{update } q_i \text{ to maximize } L_i(p,q_i) & \scriptstyle{\text{; 4. also maximize } q_i \text{how? -> will talk bout this later}} \\ \end{aligned}\]
우리가 힘겹게 목적 함수도 정의 했으며, 어떻게 파라메터를 업데이트 하는지 까지 알아보긴 했지만, 여기서 문제가 하나 있습니다. 예를 들어, 우리가 \(q_i\)를 간단한 분포, 즉 아래와 같은 세팅의 가우시안 분포라고 가정해보도록 하겠습니다.
\[q_i(z) = N(\mu_i, \sigma_i)\]여기서 주의해야 할 점은 \(p(z)\)와 \(q_i(z)\)는 다르다는 겁니다. \(p(z)\)는 파라메터가 없는 \(N(0,I)\) 이고, \(q_i\)는 데이터 포인트 \(x_i\)에 대한 파라메터화 된, 즉 학습을 통해 우리가 추정해야 하는 분포인거죠. 우리는 각 데이터 포인트 \(x_i\)마다 평균, \(\mu_i\) 와 분산, \(\sigma_i\)이 필요합니다.
즉 이는 데이터 포인트가 하나의 이미지라면, 모든 이미지 마다 가짜 정답 (fake label)을 달아주는 것 (annotate)이 되는 겁니다.
그러니까 우리는 \(L_i\)를 \(q_i\)에 대해 업데이트 하려면 아래와 같이 모든 이미지 마다, 두 파라메터를 전부 다 업데이트 해야 하는 겁니다.
(한 데이터 포인트마다 샘플링을 여러번 하면 이 과정은 더 오래걸리겠죠?)
- use gradient \(\bigtriangledown_{\mu_i} L_i(p,q_i)\) and \(\bigtriangledown_{\sigma_i} L_i(p,q_i)\)
- gradient ascent on \(\mu_i,\sigma_i\)
우리가 지금까지 정의하고 사용하려는 방법론이 클래식한 변분법이며 분명히 작용하는 알고리즘이겠지만, 이는 업데이트해야 할 파라메터가 너무 많다는 단점이 있습니다.
- How many parameters are there? \(\vert \theta \vert + ( \vert \mu_i \vert + \vert \sigma_i \vert ) \times N\)
즉 \(p_\theta(x_i \vert z)\)를 모델링한 신경망의 모델 파라메터 \(\theta\)개수에 각 데이터 포인트 마다 평균, 분산 2개의 파라메터가 추가적으로 있는거죠.
이는 데이터가 많으면 많을수록 더 다루기 힘들어 질 것입니다.
그렇다면 이를 해결하기 위해서는 어떻게 해야할까요? 네 맞습니다, \(x_i\)마다 \(q_i\)를 정하지 말고, 이 둘 사이 관계를 매핑해주는 신경망을 하나 더 두는 것이죠.
- intuition : \(q_i(z)\) should approximate \(p(z \vert x_i)\) then what if learn network \(q_i (z) = q(z \vert x_i) \approx p(z \vert x_i)\)?
바로 두 가지 네트워크를 둬서 approximate하는 것이 변분법을 사용하는 생성 모델, VAE의 핵심입니다.
\[q_i (z) = q(z \vert x_i) \approx p(z \vert x_i)\] Fig. \(x \rightarrow z\)로 매핑해주는 Encoder Network, \(z \rightarrow x'\), 즉 생성을 담당하는 Decoder Network 두 가지를 학습하면 된다.
Fig. \(x \rightarrow z\)로 매핑해주는 Encoder Network, \(z \rightarrow x'\), 즉 생성을 담당하는 Decoder Network 두 가지를 학습하면 된다.
Amortized Variational Inference
이제 우리는 두 가지 네트워크를 가지게 되었죠.

그렇기 때문에 ELBO 수식도 조금 변경해야할 필요가 있습니다.
모든 데이터 포인트 마다 근사 분포를 가지고 있던 일반적인 변분 추론 (Regular Variational Inference)를 \(q_{\phi}\)라는 네트워크 하나로 바꾸면
\[\begin{aligned} & log p(x_i) \geq \mathbb{E}_{z \sim q_i(z)} [log p(x_i \vert z) + log p(z)] + H(q_i) & \\ & \geq \mathbb{E}_{z \sim q_{\phi}(z \vert x_i)} [log p(x_i \vert z) + log p(z)] + H(q_{\phi}(z \vert x_i)) & \end{aligned}\]위와 같은 일반화된 수식을 얻을 수 있습니다.
(주의해야 할 점은 \(p(z)\)는 prior로 (일반적으로 ML 사용되는 prior 개념 맞습니다.) 변하지 않는 분포입니다. 즉 파라메터가 없습니다. 바뀐건 \(q_i\) 입니다.)
이로써 ELBO가 아래와 같이 새로 정의됐습니다.
목적 함수가 바뀌었으니 업데이트 하는 training procedure도 바뀌었겠죠?
\[\begin{aligned} & \text{for each } x_i (\text{ or mini-batch}): & \\ & \quad \text{calculate } \bigtriangledown_{\theta} L(p_{\theta}(x_i \vert z), q_{\phi}(z \vert x_i)): & \\ & \quad \quad \text{sample } z \sim q_{\phi}(z \vert x_i) & \\ & \quad \quad \bigtriangledown_{\theta} L \approx \bigtriangledown_{\theta} log p_{\theta} (x_i \vert z) & \\ & \quad \theta \leftarrow \theta + \alpha \bigtriangledown_{\theta} L & \\ & \quad \phi \leftarrow \phi + \alpha \bigtriangledown_{\phi} L & \end{aligned}\]
(크게 다를 바 없으니 천천히 음미해 보시면 될 것 같습니다.)
자, 이제는 정말 거의 다 왔습니다. 마지막 문제점 하나만 해결하면 잠재 변수 모델을 학습시킬 수 있는데요, 그것은 바로 어떻게 \(q_{\phi}\) 네트워크의 미분을 계산할까? 입니다.
- how \(\phi \leftarrow \phi + \alpha \bigtriangledown_{\phi} L\) ???
Re-Parameterization Trick
ELBO에서 \(\phi\)는 두 곳에서 사용됩니다.
하나는 기대 값을 계산할 때 샘플링을 하는 분포이며, 다른 하나는 두번째 term인 엔트로피를 계산할 때 입니다. 여기서 두 번째 엔트로피를 계산하는 term은 쉽게 계산할 수 있습니다. (tensorflow나 pytorch 같은 딥러닝 프레임워크를 사용하면 간단하게 자동으로 미분해줍니다.)
하지만 문제는 기대 값을 계산하는 부분에서 발생합니다.
기대 값 안의 수식은 \(\phi\)와 관련이 없지만 바로 샘플링 (sampling)을 하는데 \(z \sim q_{\phi}\) 부분에서 문제가 발생하는 건데요,
왜냐하면 이러한 샘플링을 하는 과정은 미분 불가능 (non-differentiable) 하기 때문에 gradient를 끝에서 끝까지 전파할 수 없기 때문입니다.
이에 대해서 조금 더 논하기 위해서 수식을 아래와 같이 조금 바꾸도록 하겠습니다.
\[\begin{aligned} & J(\phi) = \mathbb{E}_{z \sim q_{\phi} (z \vert x_i)} [log p(x_i \vert z) + log p(z)] & \\ & J(\phi) = \mathbb{E}_{z \sim q_{\phi} (z \vert x_i)} [r(x_i,z)] & \end{aligned}\]기대 값 내부의 수식이 \(r(x_i,z)\)로 바뀌었습니다.
사실 다른 알파벳을 사용할 수도 있었지만 \(r\)로 표현한 이유가 있습니다.
그것은 바로 이 기대 값이 나타내는 바가 어떠한 분포에서 행동과 상태를 샘플링을 하고, 이를 이용해 보상값을 계산해서 평균내는 강화 학습의 기본 목적함수와 닮았기 때문입니다.
그래서 보상을 의미하는 reward의 이니셜 r을 따온 것이며, 또한 강화 학습의 정책 경사 (Policy Gradient)알고리즘인 REINFORCE알고리즘이 미분 불가능한 알고리즘을 다루기 좋은 방법론이기 때문에, 겸사겸사 원 수식을 강화 학습처럼 나타낸 것입니다.
REINFORCE를 사용한 Objective Function, ELBO의 미분형태는 아래와 같은데요,
\[\begin{aligned} & J(\phi) = \mathbb{E}_{z \sim q_{\phi} (z \vert x_i)} [r(x_i,z)] & \\ & \bigtriangledown J(\phi) = \frac{1}{M} \sum_j \bigtriangledown_{\phi} log q_{\phi} (z_j \vert x_i) r(x_i, z_j) & \end{aligned}\]우리가 강화학습을 다루는 게 아니기 때문에 여기까지만 하고 미분 불가능한 함수를 다루는 다른 방법론에 대해서 알아보긴 할 것이지만,
조금만 설명을 보태자면 바로 위의 수식은 크로스 엔트로피 (Cross Entropy, CE) 손실함수의 각 클래스 마다 보상 (reward) 이라는 값을 곱해준, 즉 weighted sum한 수식이라고 할 수 있습니다.
그리고 정책 경사 알고리즘은 일반적으로 variance가 크다는 문제점 등이 있는데, 물론 잠재 변수 \(z\)를 여러번 샘플링 하는 방법으로 이를 줄일 수 있지만, 이보다 더 빠르고 실용적이며 범용적인데다가, 강화 학습 알고리즘과는 다르게 \(r\)의 미분값을 직접적으로 계산할 수 있는 방법이 있으니, 바로 앞으로 설명 할 Re-Parameterization Trick 입니다.
우리가 추론하고 싶은 분포는 \(\phi\)로 파라메터화 된 가우시안 분포이죠.
여기서 샘플링을 하는 연산 (Sampling Operation)을 바로 아래와 같이 수정할 수 있는데요,
바로 \(\phi\)와 관련없는 다른 \(N(0,1)\)에서 랜덤 샘플링을 한 뒤 (\(\epsilon \sim N(0,1)\)) \(\mu_{\phi}\)에 더해주는 겁니다.
이렇게 되면 \(z\) 자체를 평균과 분산에 대한 deterministic function으로 나타낼 수 있고, \(\epsilon\)만 stochastic합니다.
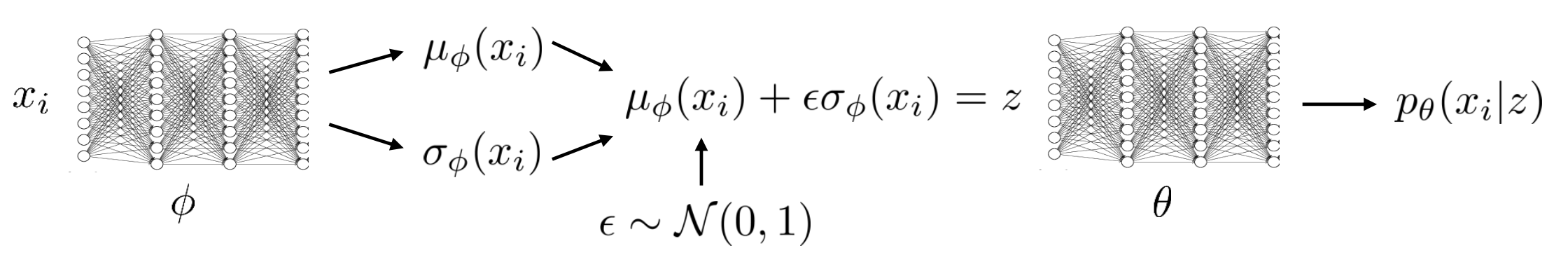 Fig. Reparametarization Trick
Fig. Reparametarization Trick
이렇게 할 경우 분포로부터 샘플링 하는 stochastic함을 유지하면서도, 직접적으로 샘플링을 하는게 아니며 \(\epsilon\)은 네트워크와 관련이 없는 랜덤 변수이기 때문에 \(\phi\)에 미분을 전파하는데 전혀 문제가 없습니다.
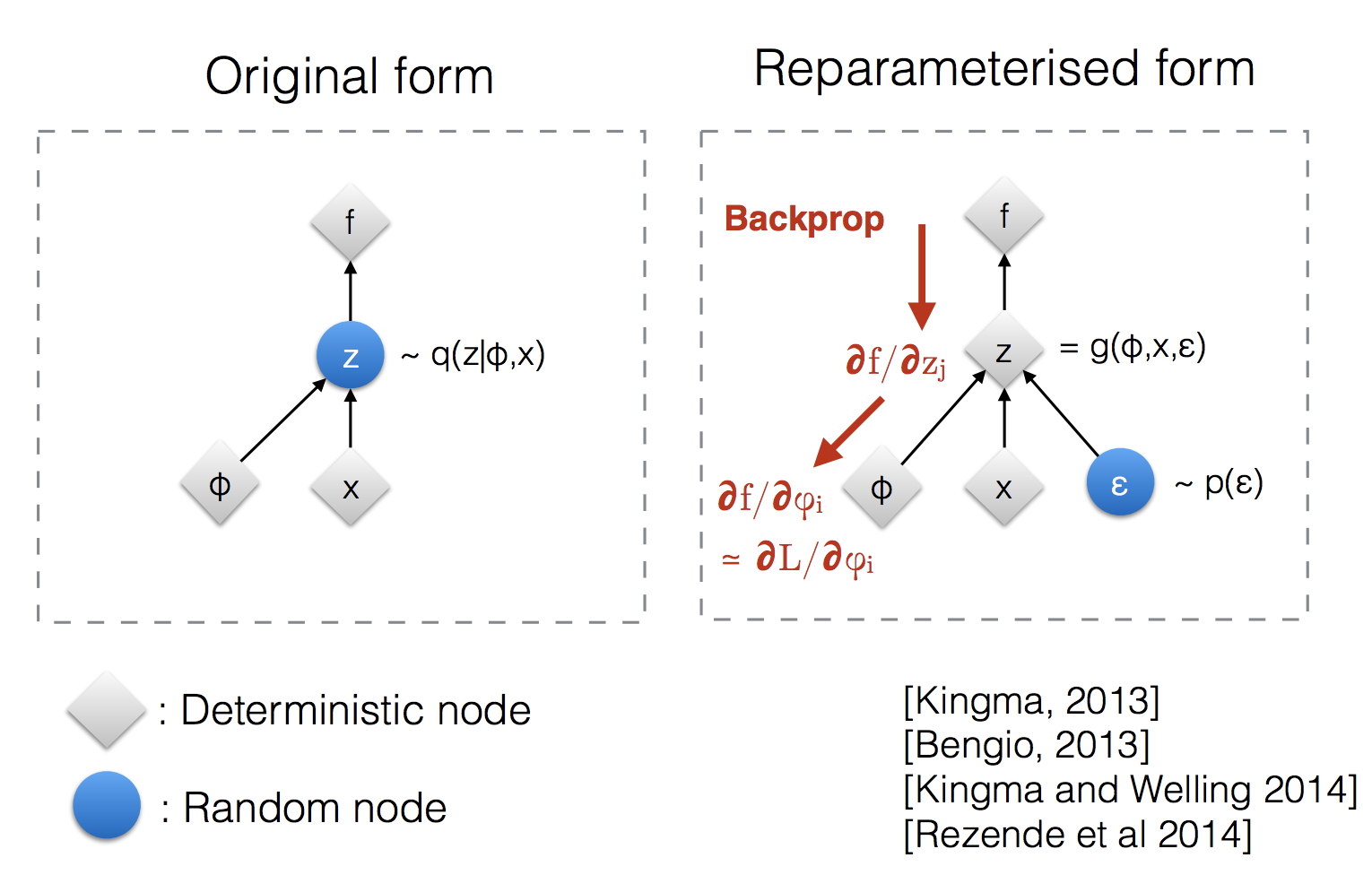 Fig. Error Backpropagation of Re-Parameterization Trick. \(\epsilon\)을 샘플링 하는 것은 \(\phi\)와 별개이기 때문에 문제가 되지 않는다.
Fig. Error Backpropagation of Re-Parameterization Trick. \(\epsilon\)을 샘플링 하는 것은 \(\phi\)와 별개이기 때문에 문제가 되지 않는다.
이제 우리의 ELBO의 첫 번째 term인 기대 값 수식은 아래와 같이 수정할 수 있습니다.
이름 그대로 원래의 분포 \(z \sim q_{\phi}(z \vert x_i)\) 를 재 매개변수화 (Re-Parameterization) 한 것이 되는겁니다!
이제 이를 이용해서 training procedure에서 ELBO를 \(\phi\)에 대해서 미분하는 \(\bigtriangledown_{phi} J(\phi)\)를 아래와 같이 수정할 수 있습니다.
\[\begin{aligned} & \text{estimating } \bigtriangledown_{\phi} J(\phi) : & \\ & \quad \text{sample } \epsilon_1,\cdots,\epsilon_M \space from \space N(0,1) & \\ & \quad \bigtriangledown_{\phi} J(\phi) \approx \frac{1}{M} \sum_j \bigtriangledown_{\phi} r(x_i,\mu_{\phi} (x_i) + \epsilon_j \sigma_{\phi} (x_i)) & \end{aligned}\]
마지막으로 우리는 ELBO를 지금까지 배운 Entorpy와 KLD의 연관성과 Re-Parameterization등을 사용해서 최종적으로 아래와 같이 전개해서 표현할 수 있는데요,
우변의 두 항 중 첫 번째 항이 더 어렵고 두 번째의 KLD는 쉽게 계산할 수 있습니다. 그리고 첫 번째 항은 \(\theta\)와 \(\phi\)두 가지 모두 관여되어 있으며, 두 번째 항은 \(\phi\)만 관여되어 있습니다.
이 수식을 두 파라메터 모두에 대해서 최대화 하게 되면
 Fig. ELBO를 최대화 한다는 것의 의미
Fig. ELBO를 최대화 한다는 것의 의미
우리는 bound를 tight하게 만들면서 진짜 Objective Function을 최대화할 수 있습니다.
VAE 학습하는 방법은 다음과 같다.
- ELBO를 설정한다 (코딩한다).
- ELBO는 \(log p_{\theta}(x_i \vert z)\) 와 \(D_{KL} (q_{\phi} (z \vert x_i) \parallel p(z))\) 두 가지로 이루어져있다.
- Tensorflow나 Pytorch같은 자동 미분 패키지로 오차 역전파 (Error Backpropagation)을 통해 파라메터, \(\theta,\phi\)를 학습한다. (ELBO를 올려야 하기 때문에 경사 상승법 (gradient ascent)을 쓰면 되는데 -ELBO라면 경사 하강법을 쓸 수도 있다.)
먼 길을 달려왔지만 다시 한 번, 이 네트워크가 Variational AutoEncoder (VAE)인 이유는 아래 보이는 바와 같이 AE와 닮았기 때문입니다.
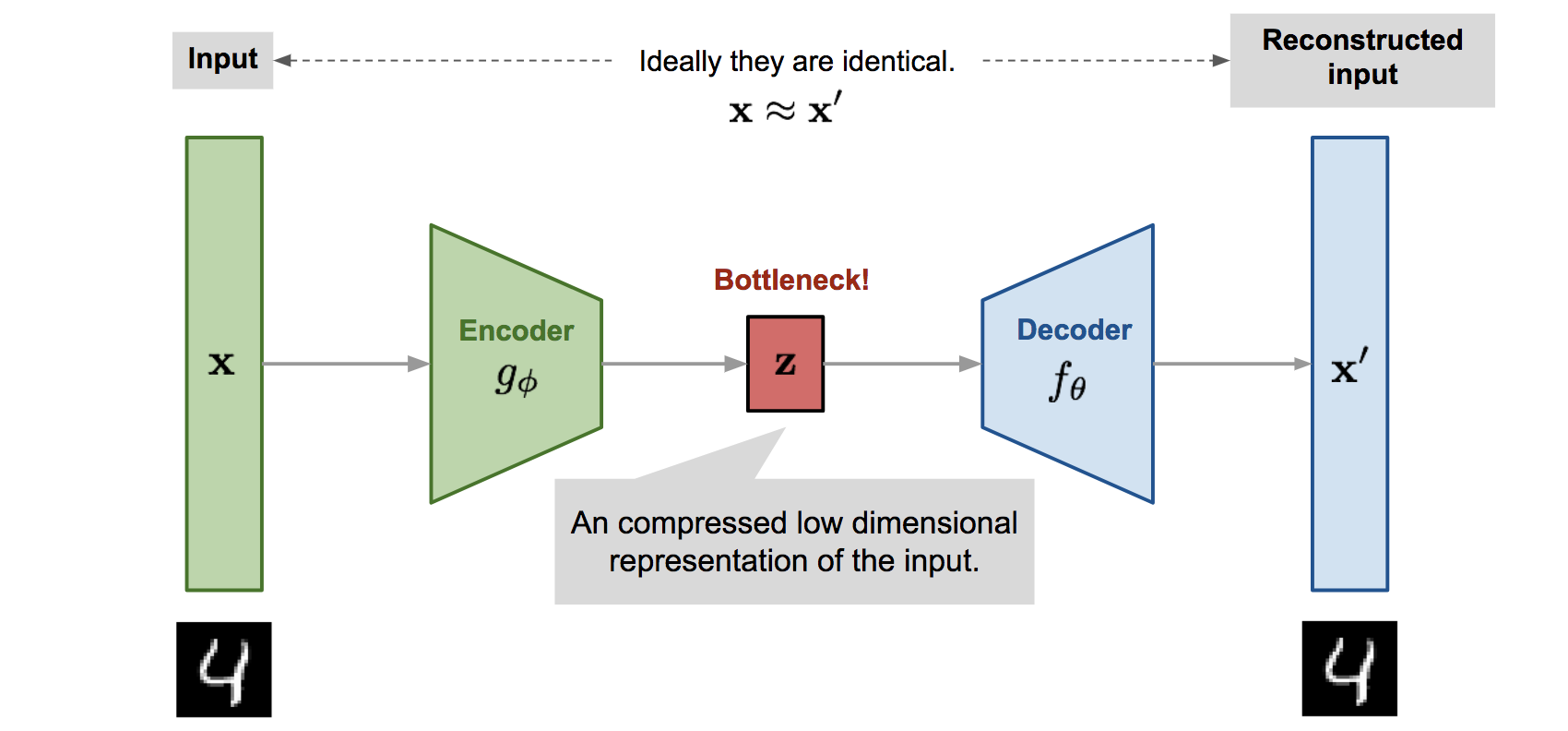 Fig. 일반적인 AutoEncoder (AE) 의 모식도
Fig. 일반적인 AutoEncoder (AE) 의 모식도
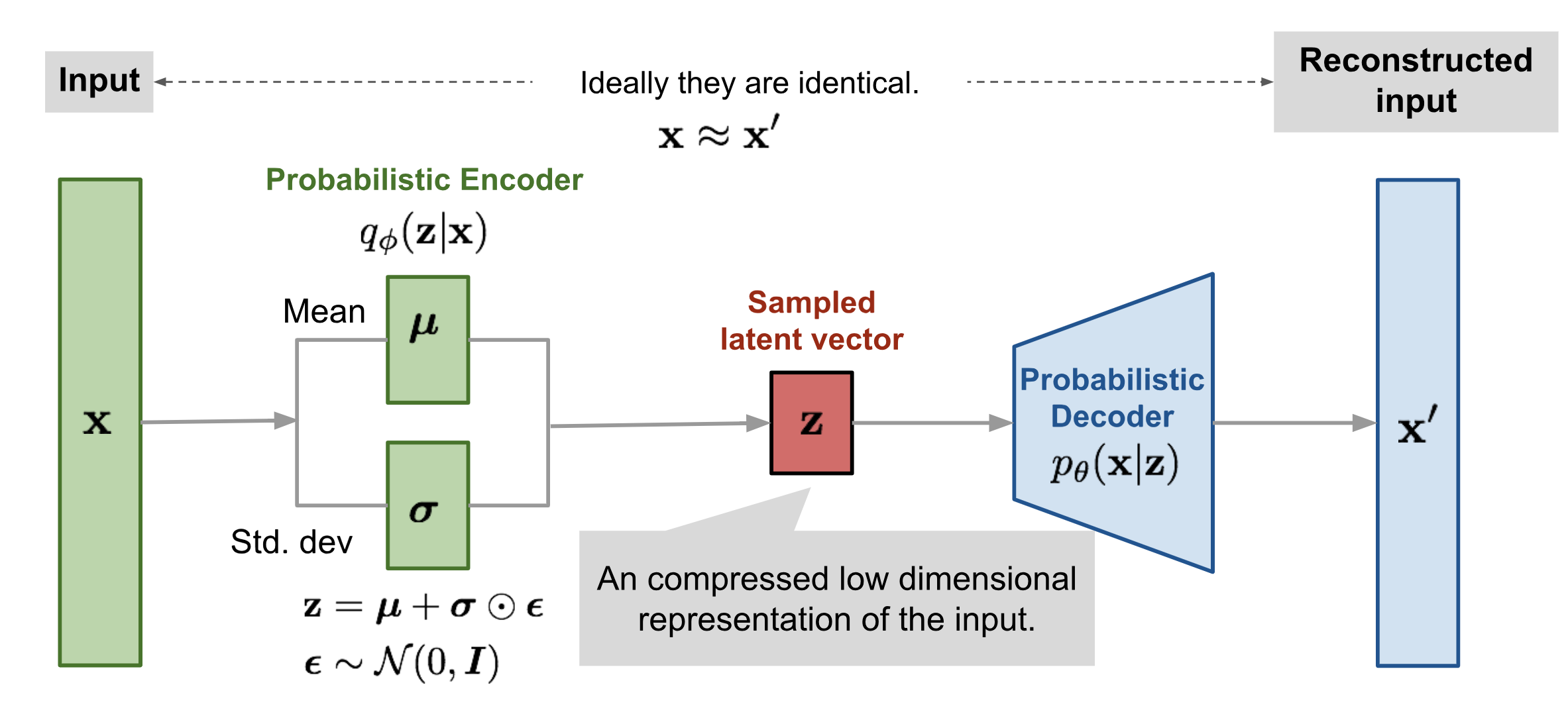 Fig. Variational AutoEncoder (VAE)의 모식도
Fig. Variational AutoEncoder (VAE)의 모식도
(DAE와 비교해서 생각해보면 VAE는 입력 단계에서 노이즈가 들어가는 DAE와 다르게, 잠재 변수 단계에서 노이즈가 들어간다.)
여기서 쓰인 Re-Parameterization Trick이 간편하고 계산의 편의성을 제공하지만
이는 연속적인 분포에 대해서만 사용 가능하다는 단점이 있으며,
반대로 짧게 소개해드렸던 정책 경사 기반의 방법론은
variance가 크지만 연속, 이산적인 분포 모두에 사용 가능하다는 장점이 있습니다.
VAE (Full)
자 이제 모든게 준비됐으니 Variational AutoEncdoer (VAE)에 대해서 다시 한 번 처음부터 끝까지 살펴보도록 하겠습니다.
VAE는 가우시안 사전 분포 \(p(z)\)를 사용하는 잠재 변수 모델 (latent variable models)의 일종 입니다.
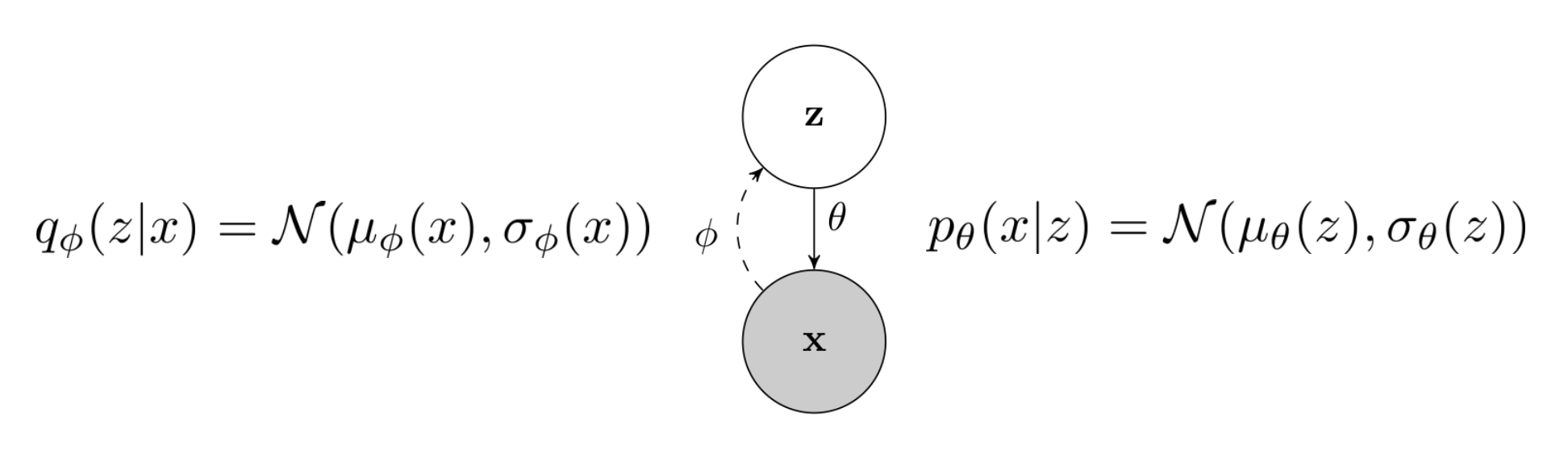 Fig. VAE
Fig. VAE
VAE를 요약하면 아래와 같습니다.
| NN | Symbol | Input | Output | param | 목적 |
|---|---|---|---|---|---|
| Encoder | \(q_{\phi}(\mathbf{z}\vert\mathbf{x})\) | x (i.e. 이미지) | \(\mu_{\phi}\),\(\sigma_{\phi}\) (가우시안으로 가정했기 때문) | \(\phi\) | x를 입력으로 분포를 추론 (Inference) |
| - | \(p(z)\) | - | - | - | 사전 분포 (Prior). \(q_{\phi}(z \vert x)\)는 이 분포를 닮아야 함. |
| Decoder | \(p_{\theta}(\mathbf{x}\vert\mathbf{z})\) | z (\(q_{\phi}(z \vert x)\)에서 샘플링한 벡터) | x (i.e. 생성된 이미지) | \(\theta\) | 이미지 생성 (Generation), 이 때 모든 픽셀에 대해서 \(\mu_{\theta}\),\(\sigma_{\theta}\) 를 독립적으로 만들어 냄. 즉, 회귀 (Regression) 문제를 푼다고 보면 됨. |
Encoder가 만들어낸 \(q_{\phi}(\mathbf{z}\vert\mathbf{x})\)가 지금은 봉우리가 한 개인 다변량 가우시안 분포 (Unimodal Multivariate Gaussian Distribution)이기 때문에 아래와 같은 분포에서 샘플링을 한다고 생각하면 됩니다.
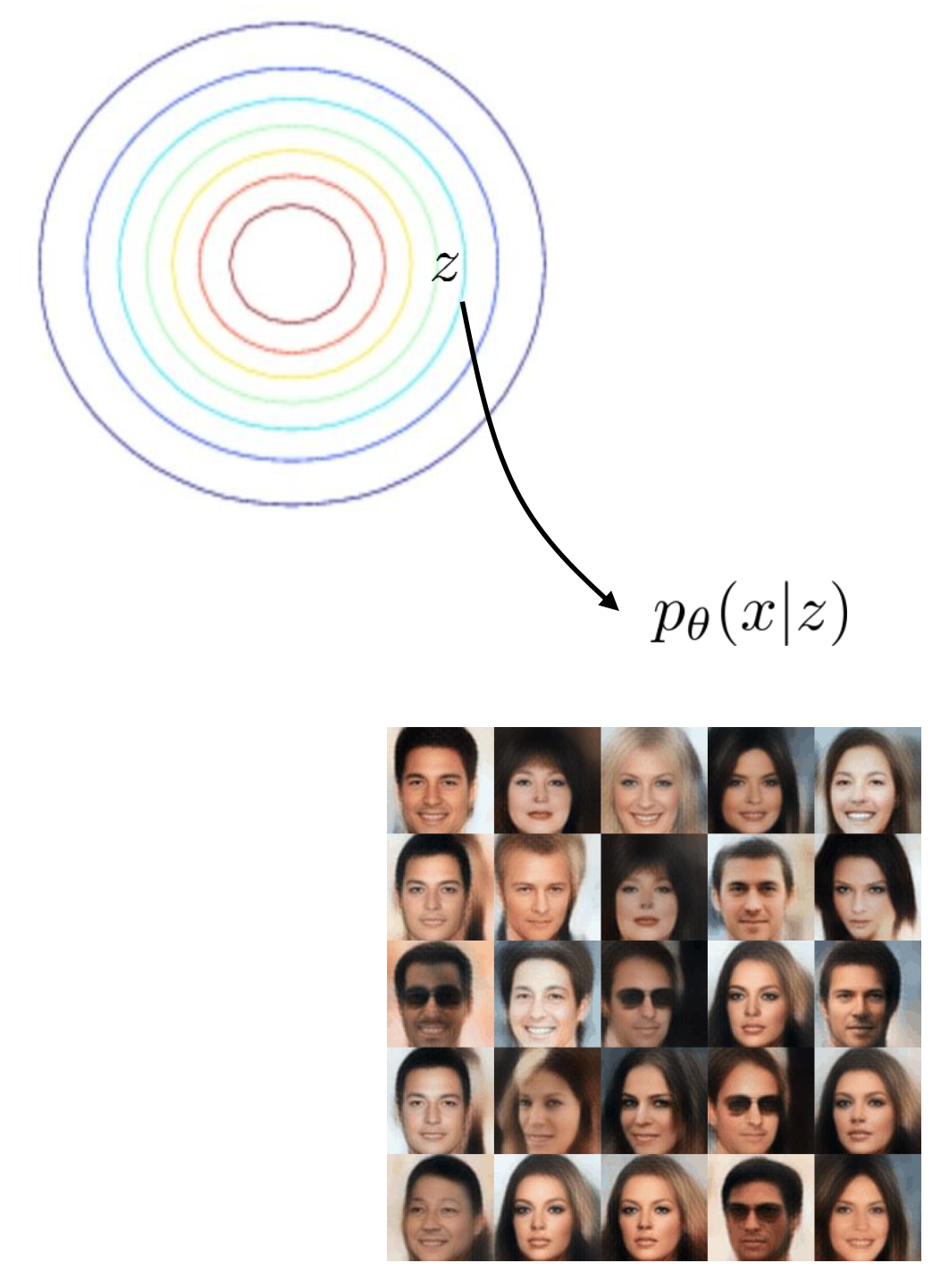 Fig. Unimodal Multivariate Gaussian Distribution으로 부터 샘플링한 벡터를 given으로 이미지를 생성한다.
Fig. Unimodal Multivariate Gaussian Distribution으로 부터 샘플링한 벡터를 given으로 이미지를 생성한다.
(물론 Unimodal Multivariate Gaussian Distribution가 아니라 봉우리가 한 10개정도 되는 Density Network를 사용해도 됩니다.)
DAE나 AE는 인코더가 차원이 축소된 히든 벡터 (Representation)를 배울 수는 있어도 이 히든 벡터를 컨트롤 해서 그럴싸한 샘플들을 (학습에 사용된 샘플을 복원하는 것 말고) 추가적으로 만들어낼 수 없으나 VAE는 가능합니다. 왜냐하면 애초에 고정된 벡터 (fixed vector)를 추출하는 AE와 다르게 (목적 자체가 고정된 벡터만 뽑으면 됐죠, 차원 축소니까), VAE는 잠재 변수의 분포를 학습했고 그 분포는 그냥 만들어 진 것이 아니라 원 데이터들이 샘플링 됐을 법한 실제 분포를 닮도록 학습이 됐기 때문입니다.
VAE는 아래와 같은 목적 함수를 최대화 하면 되는데, (이미 수차례 정의했죠)
\[\begin{aligned} & L_{VAE} = - ELBO & \\ & = - \sum_{i=1}^{N} [ log p_{\theta} (x_i \vert \mu_{\phi} (x_i) + \epsilon \sigma_{\phi} (x_i) ) - D_{KL} ( q_{\phi} (z \vert x_i ) \parallel p(z) ) ] & \\ & \hat{\theta},\hat{\phi} = arg min_{\theta,\phi} ( - \sum_{i=1}^{N} [ log p_{\theta} (x_i \vert \mu_{\phi} (x_i) + \epsilon \sigma_{\phi} (x_i) ) - D_{KL} ( q_{\phi} (z \vert x_i ) \parallel p(z) ) ] ) & \end{aligned}\]이를 그림으로 디테일하게 나타내면 아래와 같이 됩니다.
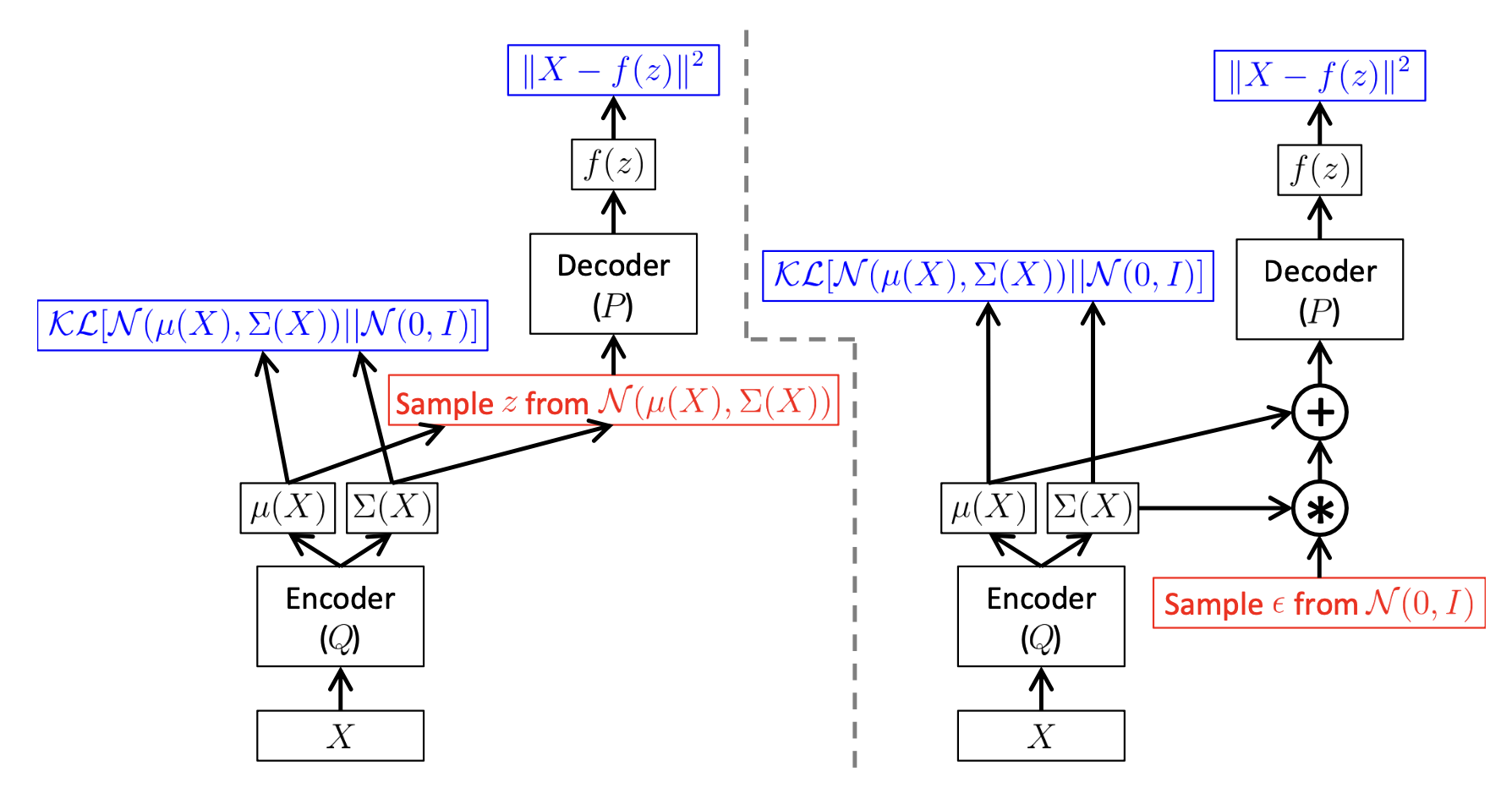 Fig. VAE in Training Time
Fig. VAE in Training Time
그리고 학습이 끝난 후에는 아래처럼 가우시안 분포에서 샘플링해서 전에 없던 데이터를 만들어내면 됩니다. (이 잠재 변수가 해석이 가능한가? 어떻게 컨트롤 해야 하는가?는 다음에 알아보도록 하겠습니다.)
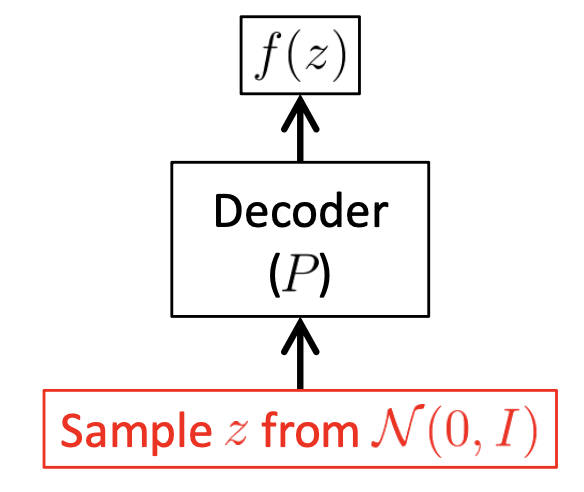 Fig. VAE in Test Time
Fig. VAE in Test Time
Test time 에서 인코더는 사용되지 않습니다.
\[\begin{aligned} & \hat{\theta},\hat{\phi} = arg max_{\theta,\phi} ( \sum_{i=1}^{N} [ log p_{\theta} (x_i \vert \mu_{\phi} (x_i) + \epsilon \sigma_{\phi} (x_i) ) - D_{KL} ( q_{\phi} (z \vert x_i ) \parallel p(z) ) ] ) & \\ & \hat{\theta},\hat{\phi} = arg min_{\theta,\phi} ( - \sum_{i=1}^{N} [ log p_{\theta} (x_i \vert \mu_{\phi} (x_i) + \epsilon \sigma_{\phi} (x_i) ) - D_{KL} ( q_{\phi} (z \vert x_i ) \parallel p(z) ) ] ) & \end{aligned}\]이 수식에서 첫 번째 term은 ‘이미지를 잘 만들도록 학습해라’ 라는 의미를 가지기 때문에 Reconstruction Error term이라고 하며, 두 번째 term은 inference네트워크가 뱉는 분포가 prior \(p(z)\) 분포와 비슷해야 한다는 제약을 담고 있기 때문에 Regularization term 혹은 Penalty term 이라고 부릅니다.
여담이지만 ELBO를 \(\theta,\phi\)에 대해서 최대화 하는 방향으로 학습하는 것, 즉 번갈아가면서 인코더, 디코더를 maximize 하는 것은 EM Algorithm으로 잠재 변수 모델을 학습하는 것과 닮았습니다.
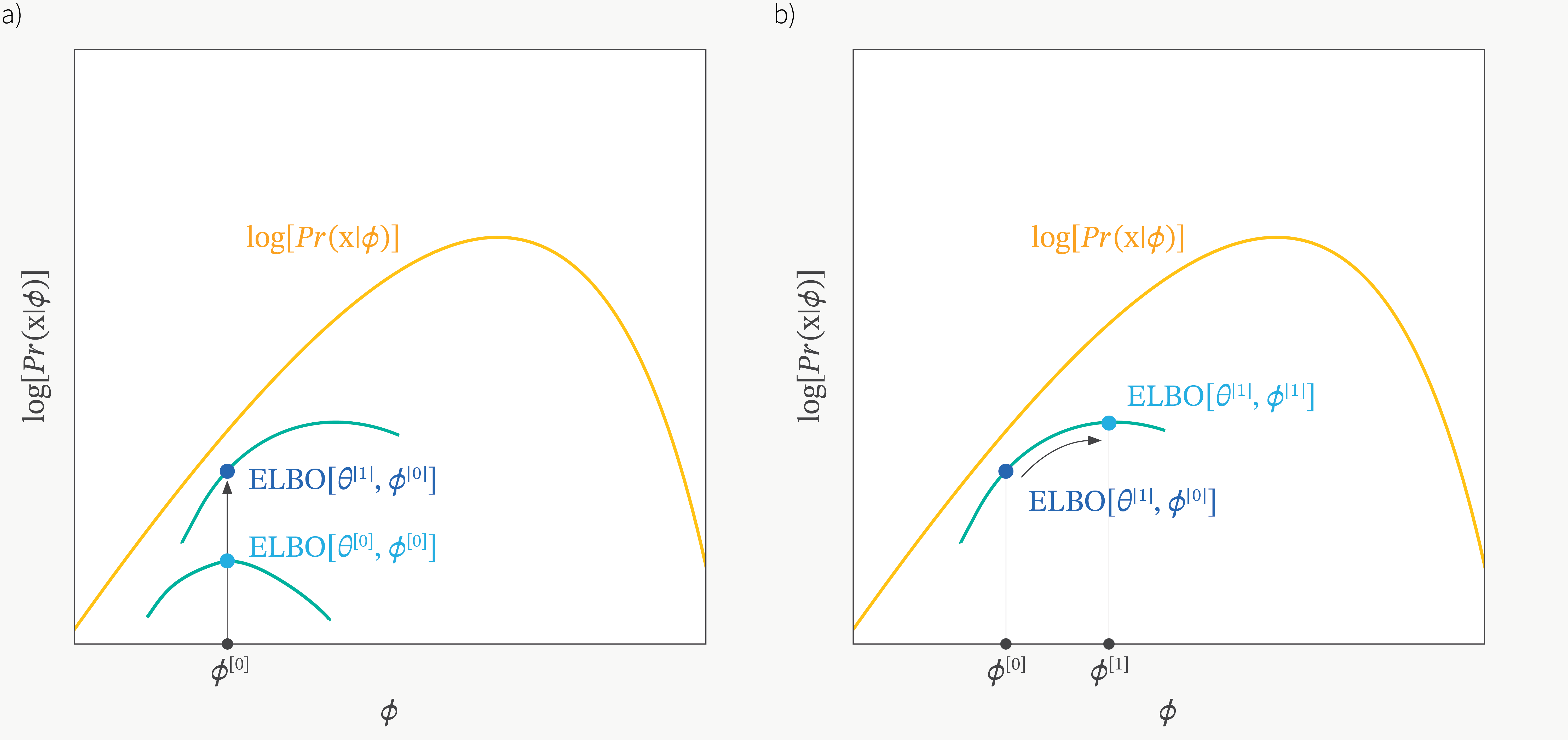 Fig. ELBO vs EM Algorithm
Fig. ELBO vs EM Algorithm
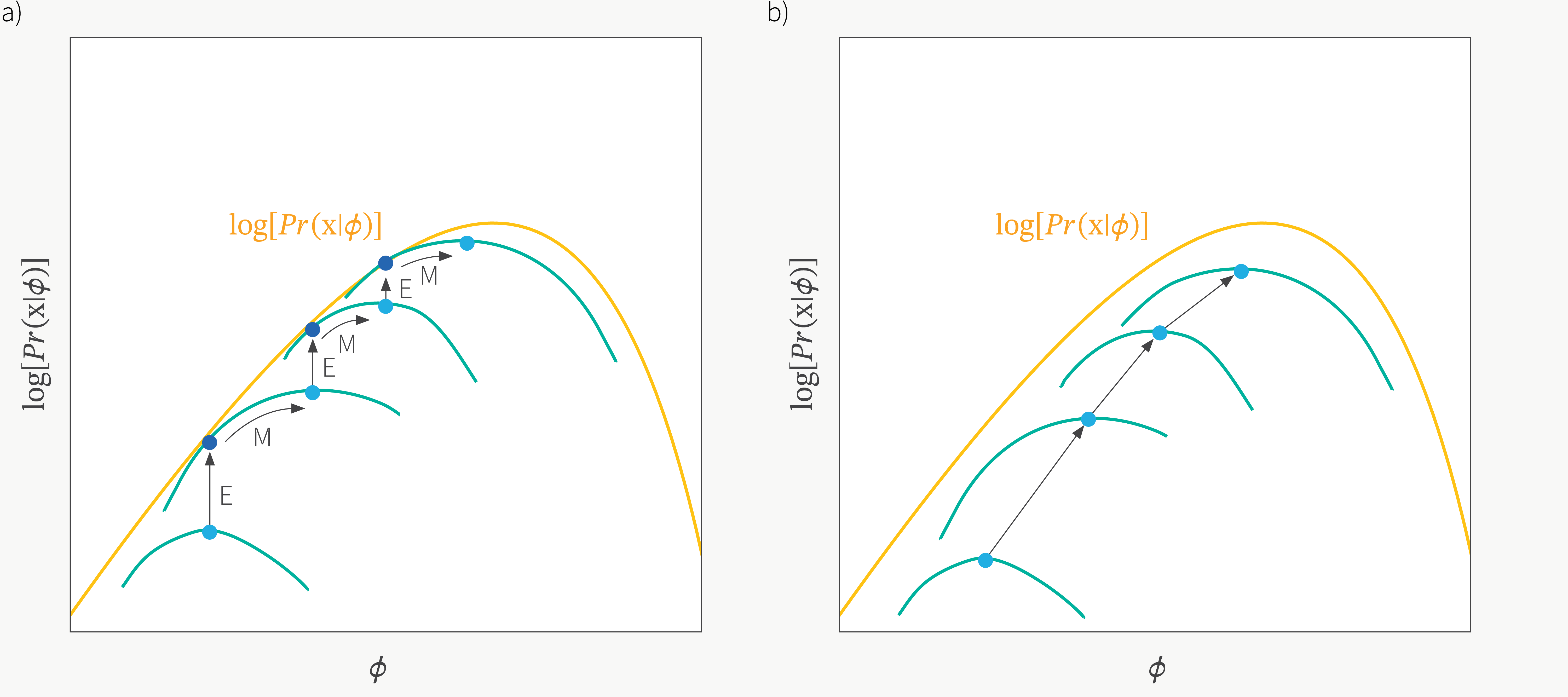 Fig. ELBO vs EM Algorithm
Fig. ELBO vs EM Algorithm
글이 너무 길어질 것 같아 자세한 이론은 생략하도록 하겠습니다. 더 궁금하신 분들은 구글링을 해보시면 좋을 것 같습니다.
Connection to AutoEncoder (AE)
Variational AutoEncoder (VAE) 는 이름에 AutoEncoder (AE) 가 들어가있습니다.
AutoEncoder (AE)는 데이터가 \(y,x\) pair 가 아니라 \(x\) 밖에 없을때 good feature 를 학습하기 위한 대표적인 비지도 학습 (Unsupervised Learning) method 중 하나 입니다.
good feature는 데이터를 저차원으로 압축했다가 다시 복원하는 과정에서 학습이 되는데,
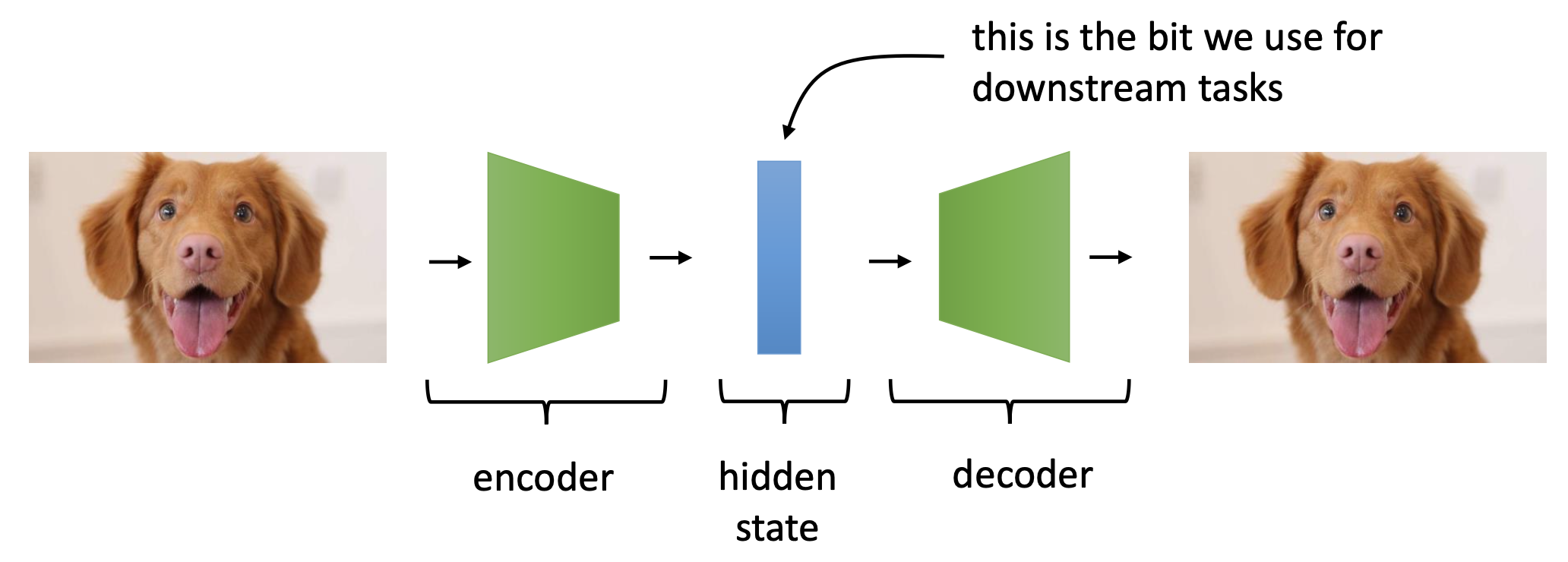 Fig. AutoEncoder (AE)
Fig. AutoEncoder (AE)
good feature는 데이터를 encoder 가 저차원으로 압축했다가 decoder가 다시 복원하는 과정에서 학습이 되는데, 이미지가 저차원에서 다시 원래 차원으로 잘 복원이 되기 위해서는 input으로부터 가장 중요한 feature만이 encoding 이 되어야 하기 때문이죠.
모델이 충분히 잘 학습되면 decoder 는 떼어버린 뒤에 linear layer 를 하나 붙혀 새로 붙혀 image classification 같은 downstream task 에 사용할 수도 있습니다. Deeplearning Era 의 BERT 같은 pre-training method의 가장 기초가 되는 방법론인거죠.
그런데 VAE 를 풀다보면 \(p_{\theta}(x \vert z)\) 와 \(q_{\phi}(z \vert x)\) 두 가지 modele, 즉 각각 \(\theta,\phi\)로 parameterize 된 neural network 들이 등장하고 \(\phi\) encoder 를 통과해서 \(\theta\) decoder 가 다시 이미지를 복원하는 모양새가 마치 AE와 비슷함을 알 수 있습니다. 하지만 VAE는 논문에서도 알 수 있듯, Variational Bayesian 방법과 Graphical Model과 관련이 있는 모델이며, 목적 자체도 오토인코더와 같이 차원축소를 목적으로 ‘저차원의 유의미한 representation을 추출한다’ 가 아니라 generative modeling 입니다. 물론 VAE 라는 생성 모델을 만드는 과정에서 학습된 encoder, \(\phi\) 를 좋은 feature extractor로 사용할 수 있지만 latent distribution 으로 부터 새로운 데이터를 sampling 할 수 있는지가 큰 차이를 만든다는 점을 유의하셔야 합니다.
VAEs with various type of decoder
VAE에서 사용되는 뉴럴 네트워크들은 분포를 출력하는 확률적인 인코더와 디코더 인데요, 그렇기 때문에 VAE의 디코더의 출력이 어떠한 확률 분포를 출력해도 상관이 없습니다. 즉 출력 분포를 베르누이 분포로 가정할 수도 있고, 가우시안 분포로 가정할 수도 있다는 거죠.
이를 MNIST 손글씨 이미지 데이터셋을 가지고 비교해서 알아보도록 하겠습니다.
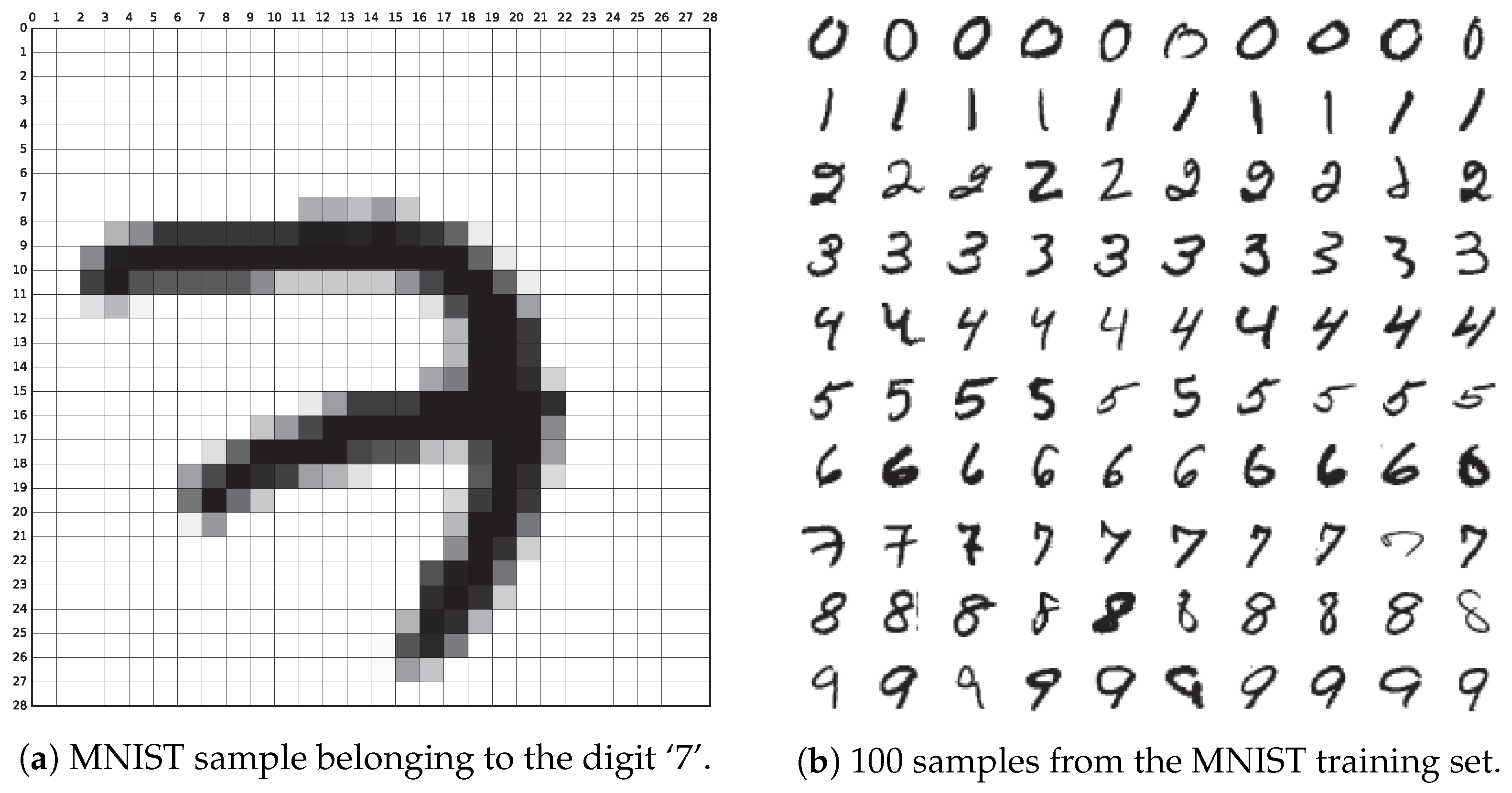 Fig. MNIST Dataset
Fig. MNIST Dataset
VAE with Gaussian Decoder
우리가 출력 픽셀들에 대한 분포를 가우시안 분포로 가정해보도록 하겠습니다.
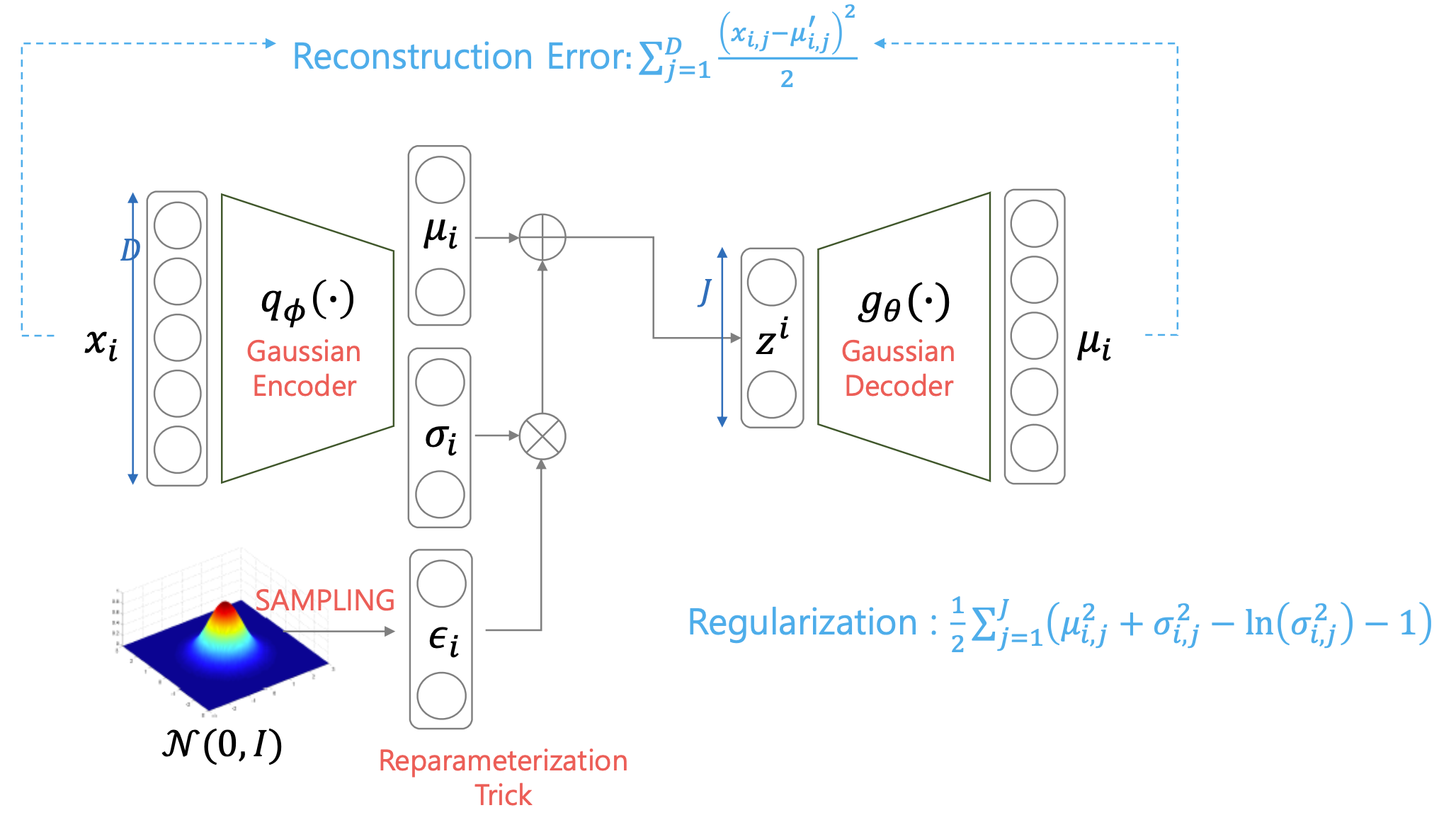 Fig. VAE with Gaussian Decoder
Fig. VAE with Gaussian Decoder
가우시안 분포로 가정을 했다는 것은 즉 회귀 문제를 풀겠다는 것이며 likelihood loss로 평균 제곱 오차 (Mean Squared Error, MSE)가 도출된다는 것을 의미합니다.
이는 ELBO에 출력 분포를 실제로 대입하면 쉽게 유도할 수 있는데요, 입출력 이미지 차원이 \(D = 28 \times 28 = 768\)차원이고, 학습 이미지 데이터의 수가 \(N\)개라고 하며, 각 학습 데이터당 \(K\)차원의 \(z\)를 딱 한번씩만 샘플링 한다고 하면,
여기서 가우시안 분포 두 개로 구성된 Regularization loss, KLD 마저 전개하면
\[\begin{aligned} & L_{VAE} = - ELBO & \\ & \approx \sum_{i=1}^{N} [ \sum_{j=1}^D ( (x_{i,j} - \mu_{i,j})^2 ) + D_{KL} ( q_{\phi} (z \vert x_i ) \parallel p(z) ) ] & \\ & \approx \sum_{i=1}^{N} [ \sum_{j=1}^D ( (x_{i,j} - \mu_{i,j})^2 ) + \frac{1}{2} ( tr(\sigma_i^2 I) + \mu_i^T \mu_i - K + ln \frac{1}{\prod_{k=1}^K \sigma_{i,k}^2 }) ] & \\ & \approx \sum_{i=1}^{N} [ \sum_{j=1}^D ( (x_{i,j} - \mu_{i,j})^2 ) + \frac{1}{2} ( \sum_{k=1}^K \sigma_{i,k}^2 + \sum_{k=1}^{K} \mu_{i,k}^2 - K + \sum_{k=1}^K ln(\sigma_{i,k}^2) ) ] & \\ & \approx \sum_{i=1}^{N} [ \sum_{j=1}^D ( (x_{i,j} - \mu_{i,j})^2 ) + \frac{1}{2} ( \sum_{k=1}^K \mu_{i,k}^2 + \sigma_{i,k}^2 - ln (\sigma_{i,k}^2) -1) ] & \\ \end{aligned}\]이 되며, 우리는 이 Objective를 \(\phi,\theta\)에 대해서 최소화 하면 (ELBO에 음수를 취했기 때문에) 됩니다.
(KLD를 직접 전개해서 closed-form으로 나타낼 때 우리가 encoder의 출력을 왜 가우시안 분포처럼 모델링 해야 하는지를 알 수 있는데요, 가우시안 분포가 아니라면 이 KLD를 이렇게 간단하게 전개하기가 힘들기 때문입니다.)
VAE with Bernoulli Decoder
그렇다면 출력 픽셀들의 분포가 베르누이 분포라면 어떨까요? 출력 분포를 베르누이 분포로 하겠다는 것은 \(0 \sim 1\) 사이의 값을 뱉는 \(p\)와 \(1-p\)로 픽셀 값을 모델링 하겠다는 겁니다.
이게 가능한 이유는 MNIST데이터셋이 \(0 \sim 1\) 사이의 값을 가지는 흑백 손글씨 이미지이기 때문입니다.
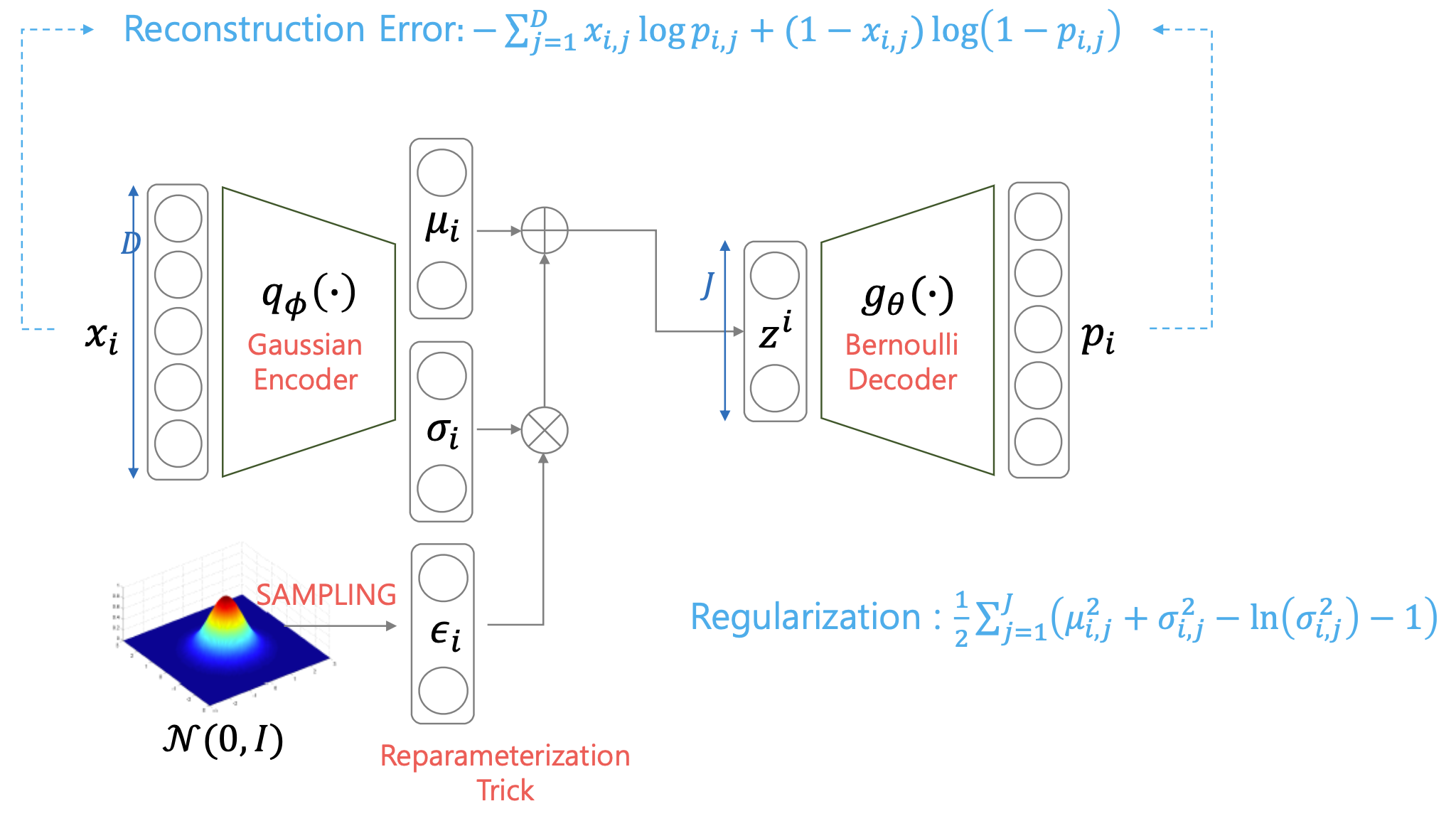 Fig. VAE with Bernoulli Decoder
Fig. VAE with Bernoulli Decoder
이를 마찬가지로 \(D\)차원 입력 이미지에 대해서 전개해보면 아래와 같이 됩니다.
\[\begin{aligned} & L_{VAE} = - ELBO & \\ & = - \sum_{i=1}^{N} [ log p_{\theta} (x_i \vert z ) - D_{KL} ( q_{\phi} (z \vert x_i ) \parallel p(z) ) ] & \\ & = - \sum_{i=1}^{N} [ \sum_{j=1}^D ( log p_{i,j}^{x_{i,j}} (1-p_{i,j})^{1-x_{i,j}} ) - D_{KL} ( q_{\phi} (z \vert x_i ) \parallel p(z) ) ] & \\ & = - \sum_{i=1}^{N} [ \sum_{j=1}^D ( x_{i,j} log p(i,j) + (1-x_{i,j}) log (1-p_{i,j}) ) - D_{KL} ( q_{\phi} (z \vert x_i ) \parallel p(z) ) ] & \\ & = \sum_{i=1}^{N} [ - (\sum_{j=1}^D ( x_{i,j} log p(i,j) + (1-x_{i,j}) log (1-p_{i,j}) ) ) + D_{KL} ( q_{\phi} (z \vert x_i ) \parallel p(z) ) ] & \\ & = \sum_{i=1}^{N} [ - (\sum_{j=1}^D ( x_{i,j} log p(i,j) + (1-x_{i,j}) log (1-p_{i,j}) ) ) + \frac{1}{2} ( \sum_{k=1}^K \mu_{i,k}^2 + \sigma_{i,k}^2 - ln (\sigma_{i,k}^2) -1) ] & \\ \end{aligned}\]여기서 출력 분포가 베르누이 분포라면 일반적으로 likelihood term이 우리가 아는 Binary Cross Entropy (BCE)가 되는데, 여기서 일반적으로 분류 모델에 사용되는 BCE와 차이점이 있다면, 정답 픽셀이 \(x \in \{ 0,1 \}\) 이 아니라 \(x \in ( 0,1 )\)라는 겁니다.
즉 모아니면 도, 검은색 아니면 흰색이 정답은 아니라는 거죠.
이렇게 출력 분포에 따라서 디코더를 모델링 할 수 있는데, 어떤 확률 분포를 가정하는 것이 더 좋다라고 하기는 어렵습니다.
 Fig. The comparison of VAES with Bernoulli Decoder and Gaussian Decoder
Fig. The comparison of VAES with Bernoulli Decoder and Gaussian Decoder
위에 그림에서 아래의 두 베르누이,가우시안 분포의 디코더를 사용한 VAE에는 생성된 이미지가 흐릿한 (blurry) 문제가 있다는 걸 알 수 있는데요,
이는 VAE의 일반적인 특성이지만 이를 해결하기 위한 방법들도 많이 제안이 되었으니 관심있으신 분들은 관련된 논문들을 찾아보시면 좋을 것 같습니다.
Why does VAE work? (Learned Manifold and Results)
VAE가 왜 work할까요? 그 이유는 직관적으로 수식의 바로 두 번째 텀인 KLD의 존재 덕분에, 우리는 \(q_{\phi}(z \vert x_i)\)을 강제로 아주 쉬운 분포인 가우시안 분포, \(p(z)\)를 닮게끔 제약하고 (penalty or regularization), 디코더 또한 이로부터 샘플링된 z를 기반으로 이미지를 생성하는 것이 훈련되어 있기 때문입니다.
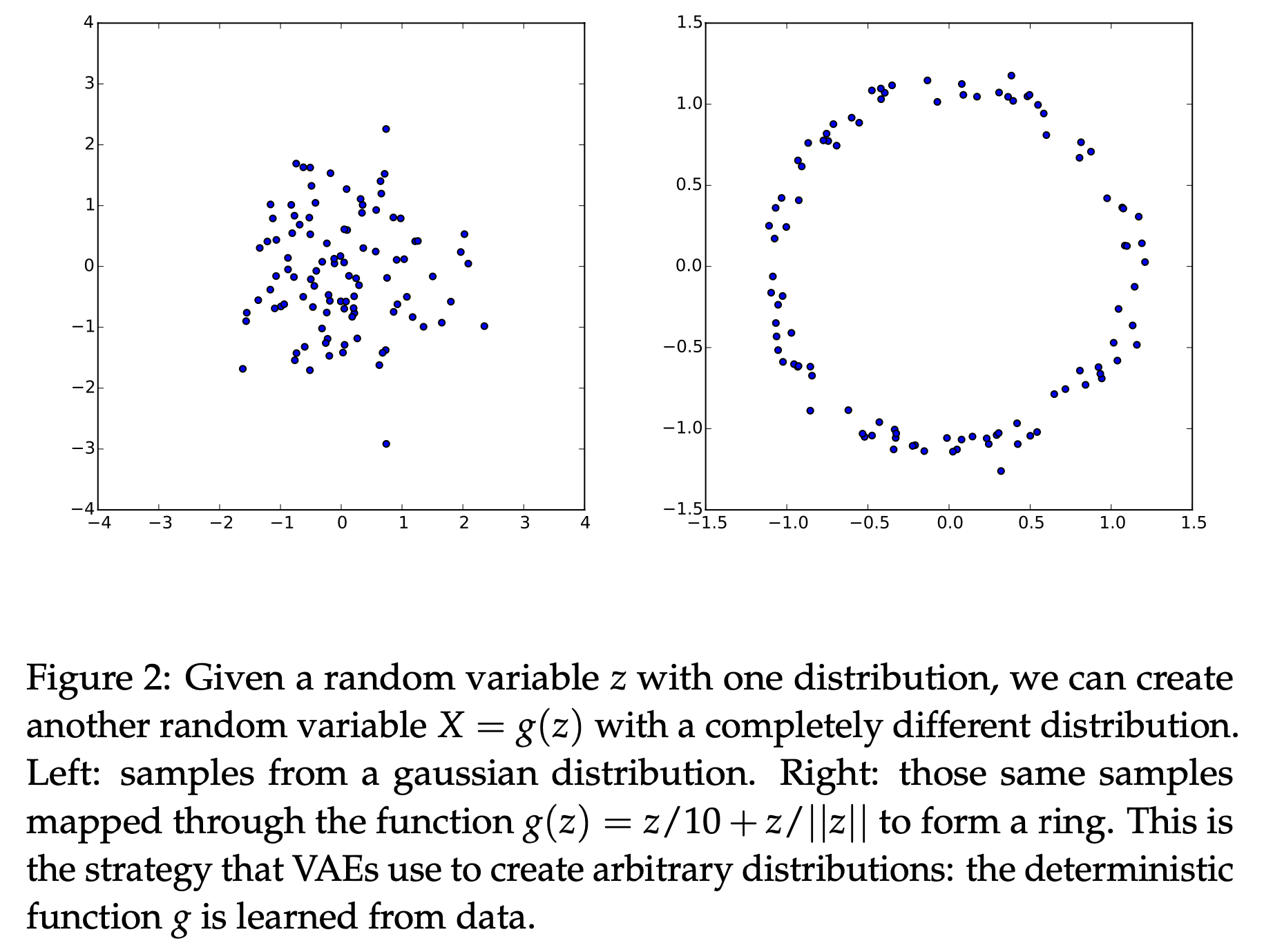 Fig. 이변량 정규 분포 (Bivariate Gasussian Distribution)에서 (좌) 샘플링 한 랜덤 변수를 입력으로 디코더는 전혀 다른 분포의 랜덤 변수를 만들게 된다(우).
Fig. 이변량 정규 분포 (Bivariate Gasussian Distribution)에서 (좌) 샘플링 한 랜덤 변수를 입력으로 디코더는 전혀 다른 분포의 랜덤 변수를 만들게 된다(우).
실제로 VAE를 통해 만들어진 \(q_{\phi}(z \vert x)\) 분포는 아래의 모양처럼 가우시안 분포를 닮았으며,
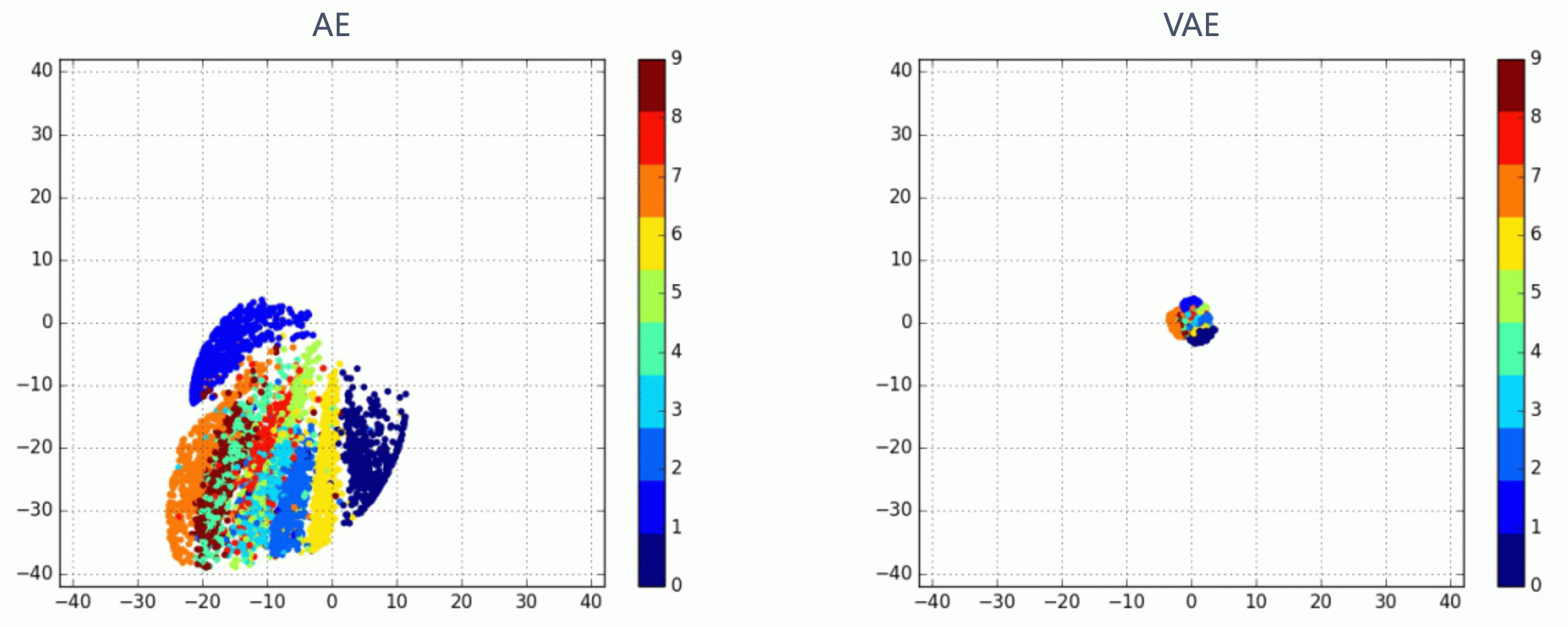 Fig. 고차원 이미지를 2차원으로 인코딩 했을 때 AE와 VAE의 차이. VAE는 2차원 정규 분포, \(N(0,I)\)로 매핑하는 강제성이 있기 때문에 평균인 0 중앙에 매핑된 벡터들이 모여있으며, 이렇게 좁은 범위 안에 뭉쳐놓는 것이 이미지를 생성하는 입장에서는 다루기가 .
Fig. 고차원 이미지를 2차원으로 인코딩 했을 때 AE와 VAE의 차이. VAE는 2차원 정규 분포, \(N(0,I)\)로 매핑하는 강제성이 있기 때문에 평균인 0 중앙에 매핑된 벡터들이 모여있으며, 이렇게 좁은 범위 안에 뭉쳐놓는 것이 이미지를 생성하는 입장에서는 다루기가 .
이를 조금 확대해 보면, MNIST 데이터셋의 서로 다른 숫자 이미지가 가우시안 분포 내에서 어떻게 형성되었는지를 알 수 있습니다.
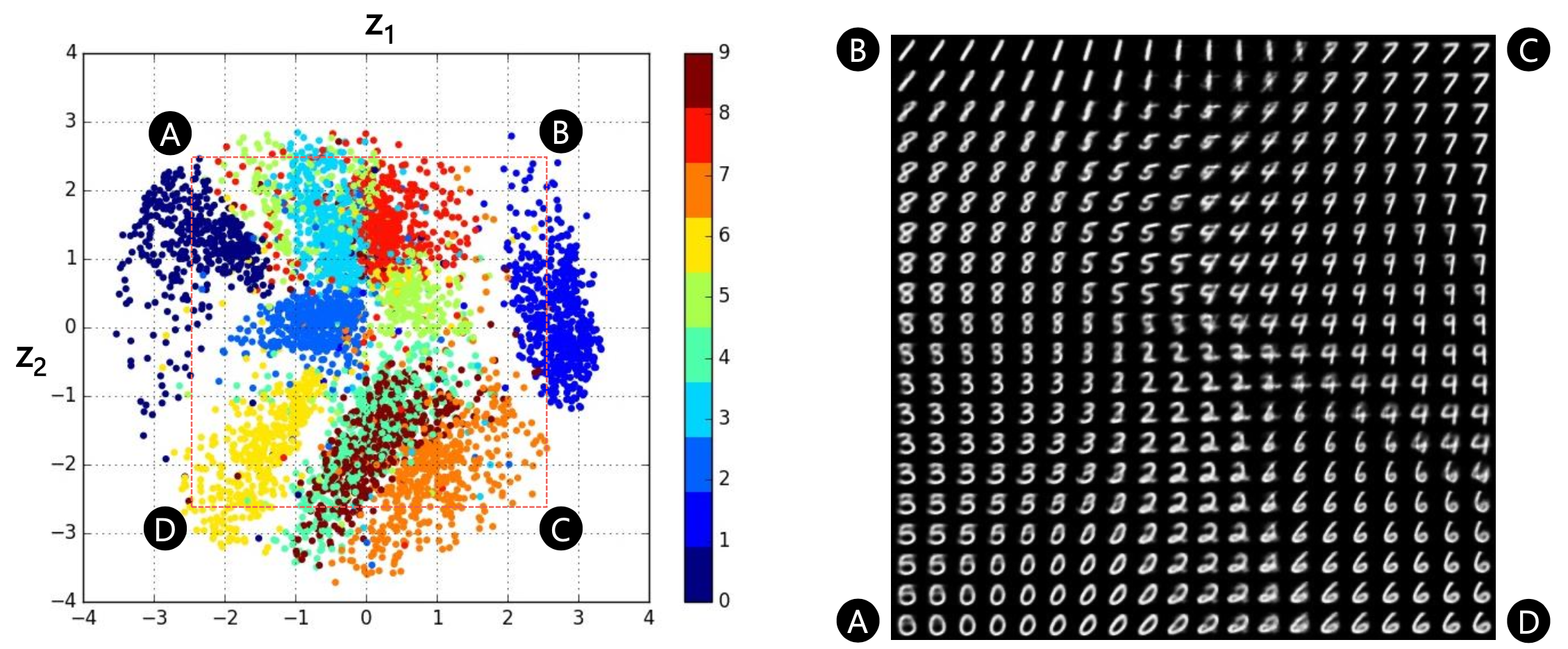 Fig. 고차원의 원본 이미지가 2차원 space에 어떻게 매핑 되었는지 알 수 있다. 이렇게 우리가 원하는 대로 가우시안 분포로 매핑되었기 때문에, test time에서 가우시안 분포로부터 샘플링한 2차원 벡터를 given으로 이미지를 생성하면 그럴싸한 이미지가 생성되는 것이다.
Fig. 고차원의 원본 이미지가 2차원 space에 어떻게 매핑 되었는지 알 수 있다. 이렇게 우리가 원하는 대로 가우시안 분포로 매핑되었기 때문에, test time에서 가우시안 분포로부터 샘플링한 2차원 벡터를 given으로 이미지를 생성하면 그럴싸한 이미지가 생성되는 것이다.
만약 KLD 텀이 없다고 생각해 볼까요?
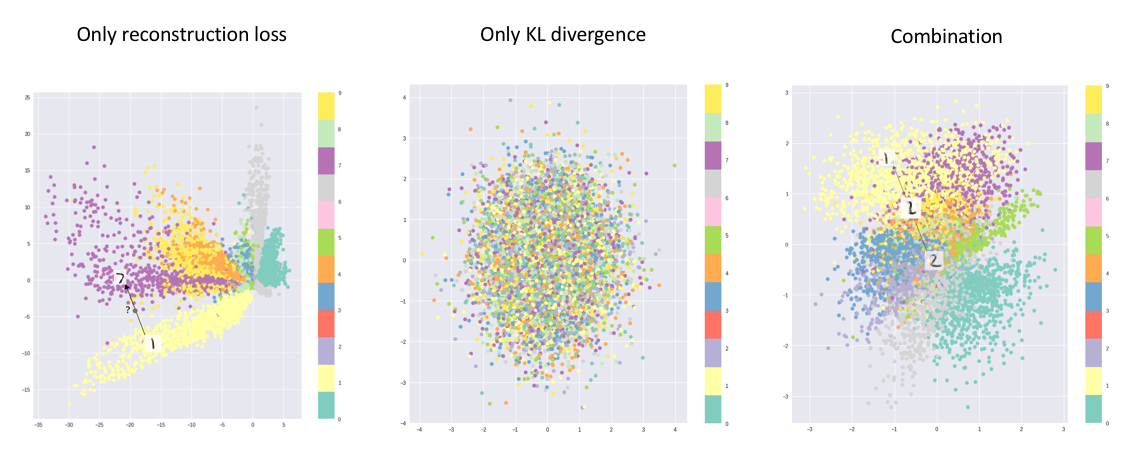 Fig. Regularization term의 존재 유무에 따른 매니폴드의 차이
Fig. Regularization term의 존재 유무에 따른 매니폴드의 차이
그렇다면 위의 사진처럼 학습된 매니폴드 상에서 의미대로 이미지가 잘 나눠지지 않는다는 걸 알 수 있습니다.
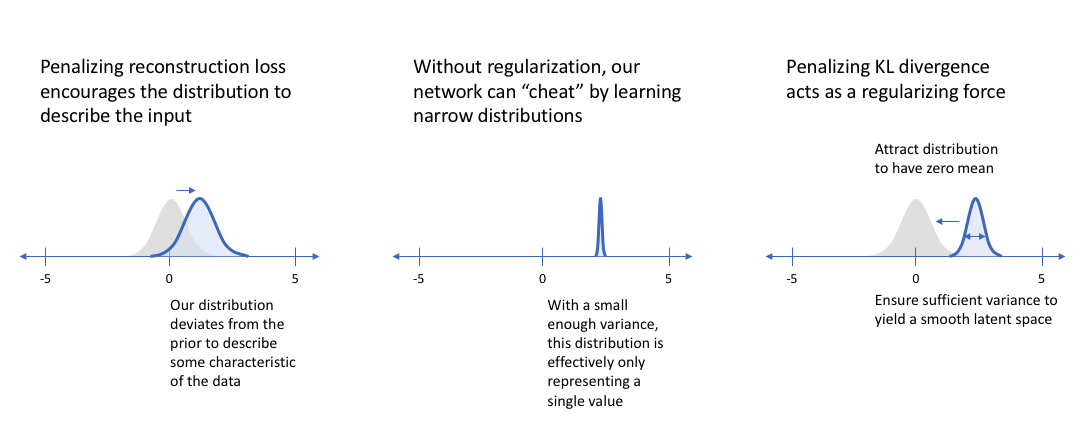 Fig. Regularization term이 중요한 이유
Fig. Regularization term이 중요한 이유
Various version of VAEs
마지막으로 VAE의 다양한 변이 네트워크 들에 대해서 간단하게 알아보고 글을 마치도록 하겠습니다.
Conditional Variational AutoEncoder (CVAE)
이번에는 Conditional VAE (CVAE)에 대해 알압도록 하겠습니다.
CVAE는 VAE의 아이디어와 크게 다르지 않습니다. 가장 큰 차이는 \(p(x)\) 를 모델링 하는 것에서 \(p(x \vert y,z)\)로 바뀌었다는 건데요,
마찬가지로 \(p(x \vert y)\) 자체는 굉장히 복잡한 분포이겠지만, \(p(x \vert y,z)\)와 \(p(z)\)는 그렇지 않을 것이며 VAE가 그랬던 것 처럼 이 두개의 다루기 쉬운 분포의 곱으로 \(p(x \vert y)\)를 나타낼 수 있을 겁니다.
- CVAE
- What we want : \(p(y \vert x) = \int p(y \vert x,z) p(z) dz\)
- Encoder : \(q_{\phi}(z \vert x_i,y_i)\)
- Decoder : \(p_{\theta}(x_i \vert y_i,z)\)
- ELBO : \(L_i = \mathbb{E}_{z \sim q_{\phi}(z \vert x_i,y_i)} [log p_{\theta}(x_i \vert y_i,z) + log p(z)] + H( (q_{\phi} (z \vert x_i,y_i) ) )\)
- Final Objective : \(\hat{\theta},\hat{\phi} = arg max_{\theta,\phi} ( \sum_{i=1}^{N} [ log p_{\theta} (y_i \vert (\mu_{\phi} (x_i,y_i) + \epsilon \sigma_{\phi} (x_i,y_i)), y_i ) - D_{KL} ( q_{\phi} (z \vert x_i,y_i ) \parallel p(z) ) ] )\)
- VAE
- What we want : \(p(x) = \int p(y \vert z) p(z) dz\)
- Encoder : \(q_{\phi}(z \vert x_i)\)
- Decoder : \(p_{\theta}(x_i \vert z)\)
- ELBO : \(L(p_{\theta}(x_i \vert z), q_{\phi}(z \vert x_i)) = \mathbb{E}_{z \sim q_{\phi}(z \vert x_i)} [log p(x_i \vert z) + log p(z)] + H(q_{\phi}(z \vert x_i))\)
- Final Objective : \(\hat{\theta},\hat{\phi} = arg max_{\theta,\phi} ( \sum_{i=1}^{N} [ log p_{\theta} (x_i \vert \mu_{\phi} (x_i) + \epsilon \sigma_{\phi} (x_i) ) - D_{KL} ( q_{\phi} (z \vert x_i ) \parallel p(z) ) ] )\)
여기서 CVAE의 경우 아래 처럼 \(x_i\)를 컨디션한 prior를 구성해도 되고
\[L_i = \mathbb{E}_{z \sim q_{\phi}(z \vert x_i,y_i)} [log p_{\theta}(y_i \vert x_i,z) + log p(z \vert y_i)] + H( (q_{\phi} (z \vert x_i,y_i) ) )\]아니어도 됩니다.
\[L_i = \mathbb{E}_{z \sim q_{\phi}(z \vert x_i,y_i)} [log p_{\theta}(y_i \vert x_i,z) + log p(z)] + H( (q_{\phi} (z \vert x_i,y_i) ) )\]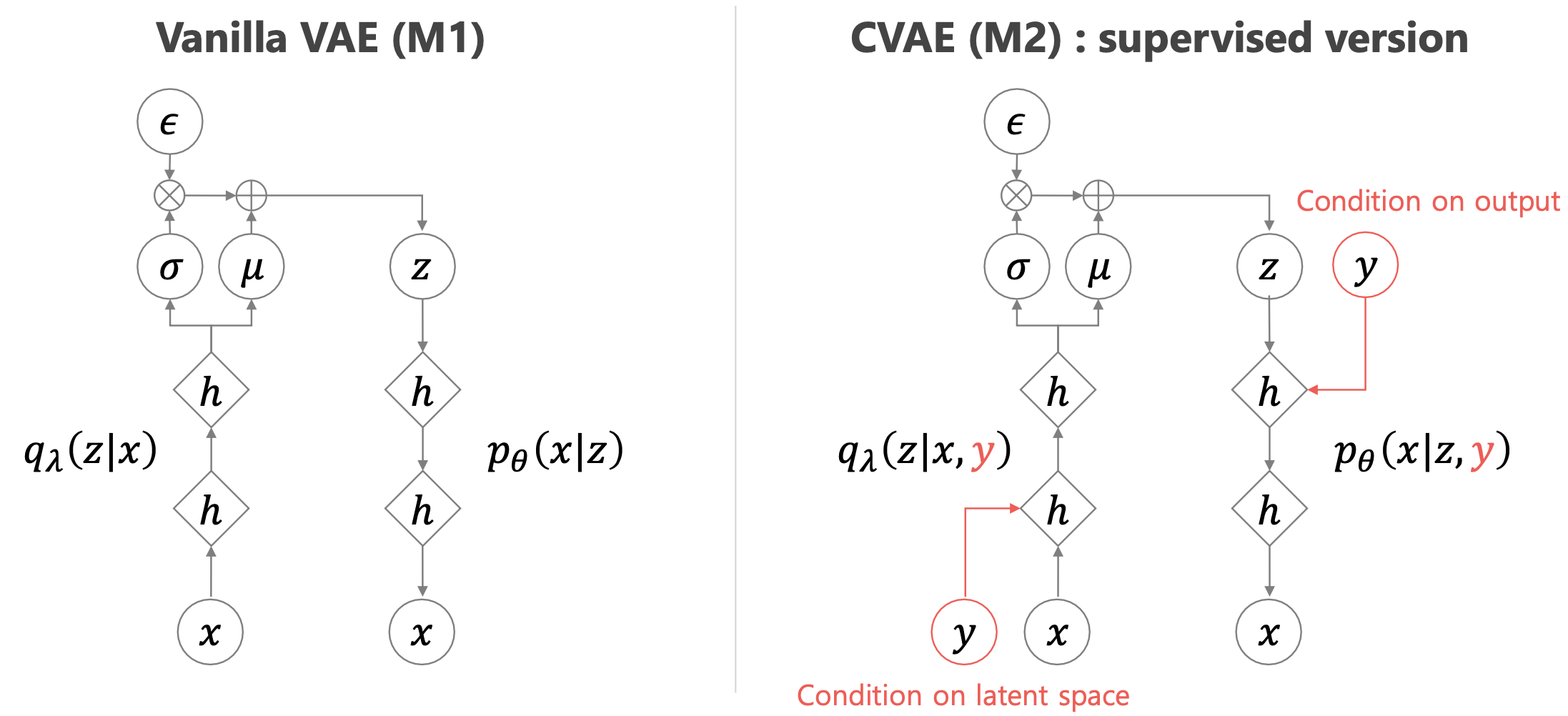 Fig. VAE vs CVAE
Fig. VAE vs CVAE
추가적으로, 데이터의 일부에 대해서만 정답을 알고있는 경우 위의 Objective처럼 Supervised가 아니라 Semi-Supervised로 문제를 풀어야 하는데 이런 경우도 크게 위에서 유도한 ELBO와 식이 다르지 않으니, 더 관심이 있으신 분들은 원본 논문 (Learning Structured Output Representation using Deep Conditional Generative Models)을 참조하시면 좋을 것 같습니다.
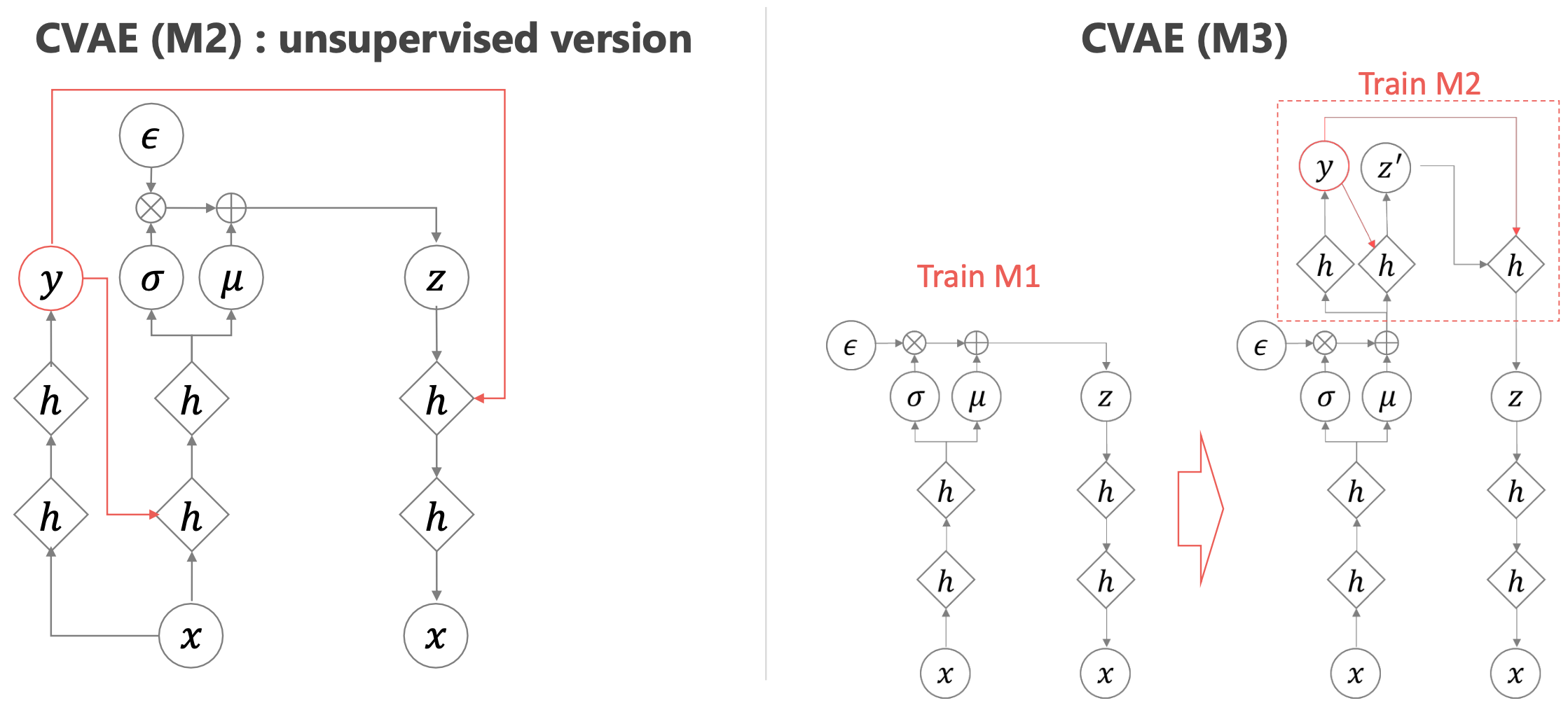 Fig. Semi-Supervised CVAE. Label이 존재하는 데이터의 경우 그대로 CVAE를 쓰되, 모를 경우 정답을 추정하는 네트워크를 별도로 추가해서 문제를 푼다. M3는 M2와 유사하지만 더욱 간단한 방법론이다.
Fig. Semi-Supervised CVAE. Label이 존재하는 데이터의 경우 그대로 CVAE를 쓰되, 모를 경우 정답을 추정하는 네트워크를 별도로 추가해서 문제를 푼다. M3는 M2와 유사하지만 더욱 간단한 방법론이다.
어쨌든, 그림을 보시면 아시겠지만 \(x\)가 VAE에서와 마찬가지로 이미지가 되겠고, \(y\)가 이미지에 대한 label같은 정보라면 (i.e. 숫자 4,5 …), 이런식으로 Auto-Encoding 학습이 된 네트워크는 근사 분포로부터 \(z\)를 뽑은 후 이미지에 대한 클래스 정보 \(y\)정보를 같이 condition해주면 우리가 원하는 이미지를 만들어 낼 수 있습니다.
이렇게 레이블 정보를 추가적으로 넣어서 학습한 CVAE는 VAE에 비해서 더욱 선명한 이미지를 만들어 내며, 네트워크의 수렴 속도도 훨씬 빠르다.
 Fig. Latent Vector의 차원이 2일 때 VAE보다 더욱 선명한 이미지를 만들어내는 CVAE.
Fig. Latent Vector의 차원이 2일 때 VAE보다 더욱 선명한 이미지를 만들어내는 CVAE.
이는 노이즈를 엄청 섞은 이미지에 대해서도 VAE보다 훨씬 잘 됩니다.
 Fig. 같은 에폭일 때 De-noising을 훨씬 잘한다.
Fig. 같은 에폭일 때 De-noising을 훨씬 잘한다.
학습 데이터로 주어지지 않은 새로운 이미지를 샘플링 하는 테스트 타임에서 CVAE의 진가가 드러나는데요, 레이블 정보를 주고 재생하는 방식으로 학습을 했기 때문에, \(z\)를 샘플링 한 뒤, 우리가 원하는 레이블 정보, \(y\)를 같이 주기만 하면 우리는 원하는 숫자 이미지를 새로 뽑을 수 있게 되는 겁니다.
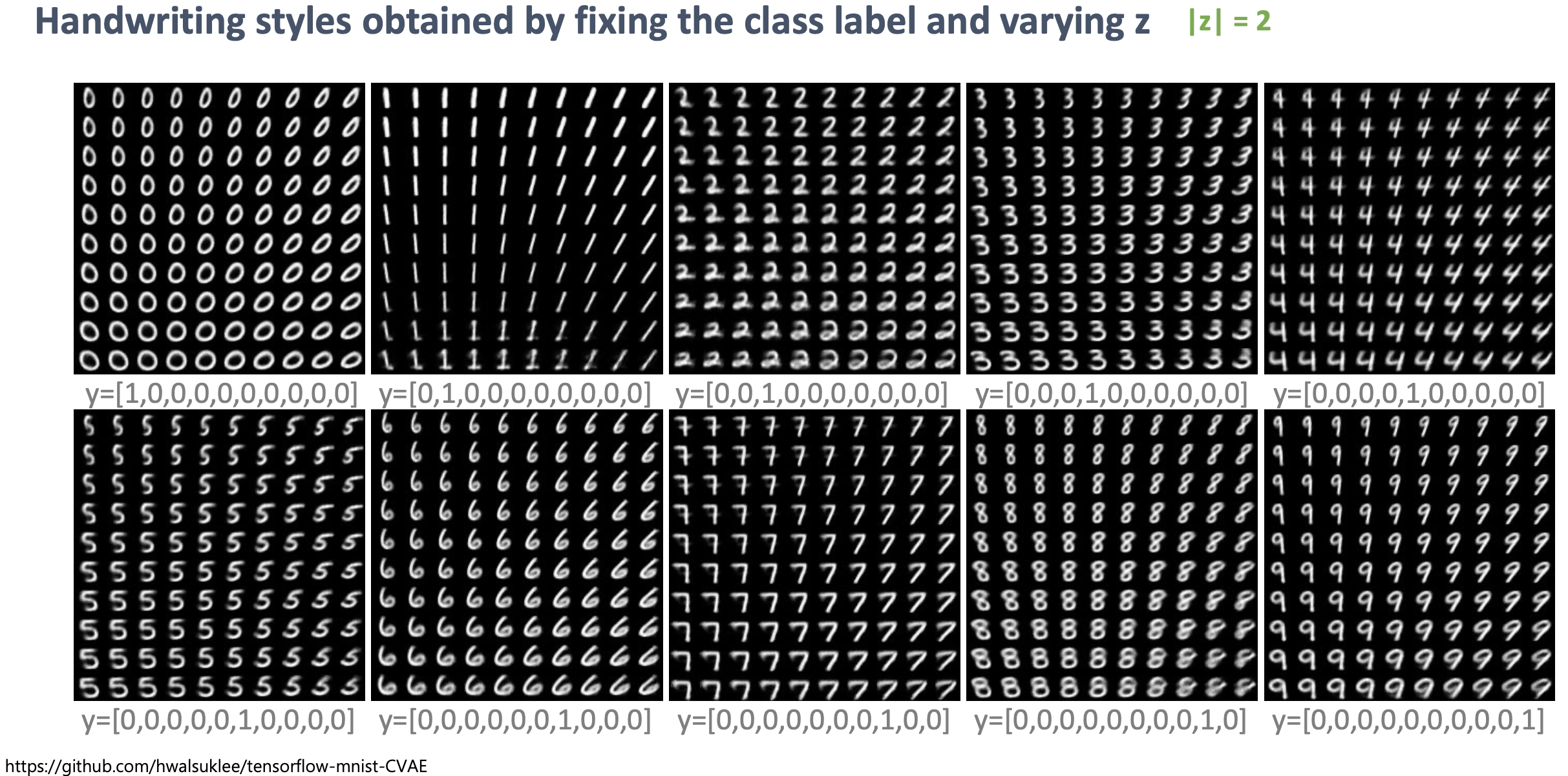 Fig. VAE에서와 다르게 z가 숫자의 회전, 기울기, 굵기 등의 공통된 feature를 담고 있는 변수가 되고, y가 숫자를 바꿀 수 있는 query가 된다.
Fig. VAE에서와 다르게 z가 숫자의 회전, 기울기, 굵기 등의 공통된 feature를 담고 있는 변수가 되고, y가 숫자를 바꿀 수 있는 query가 된다.
이는 당연하면서도 꽤나 흥미로 결과인데요, 우리가 VAE를 그냥 학습할 때는 \(z\) 분포 안에, 스타일 정보(굵기, 회전 정도, 기울기)와 숫자 label 정보가 다 같이 들어있었는데, CVAE는 이 숫자 label 정보를 \(y\)로 따로 분리한게 되는겁니다.
그래서 VAE가 아래의 그림처럼 제대로 스타일을 컨트롤하기 힘든데 반해서 CVAE는 똑같은 z를 가지고 y만 바꾼다거나 아니면 똑같은 y를 가지고 z만 바꾼다거나하는 식으로 우리가 원하는 결과를 도출해 낼 수 있다는 겁니다.
 Fig. z안에 모든 정보가 다 들어있는 VAE
Fig. z안에 모든 정보가 다 들어있는 VAE
 Fig. CVAE의 경우는 VAE와 다르게 z는 스타일 정보만, y는 숫자 label정보만 가진다. 똑같은 y를 가지고 z만 컨트롤 하면 똑같은 숫자를 다양한 스타일로 얻을 수 있다.
Fig. CVAE의 경우는 VAE와 다르게 z는 스타일 정보만, y는 숫자 label정보만 가진다. 똑같은 y를 가지고 z만 컨트롤 하면 똑같은 숫자를 다양한 스타일로 얻을 수 있다.
 Fig. 반대로 똑같은 z를 가지고 y만 컨트롤 하면 굵기, 기울기 등 스타일은 동일하지만 다른 숫자를 얻을 수 있다.
Fig. 반대로 똑같은 z를 가지고 y만 컨트롤 하면 굵기, 기울기 등 스타일은 동일하지만 다른 숫자를 얻을 수 있다.
VAE, CVAE 각 네트워크가 배우는 manifold도 아래와 같이 차이가 납니다.
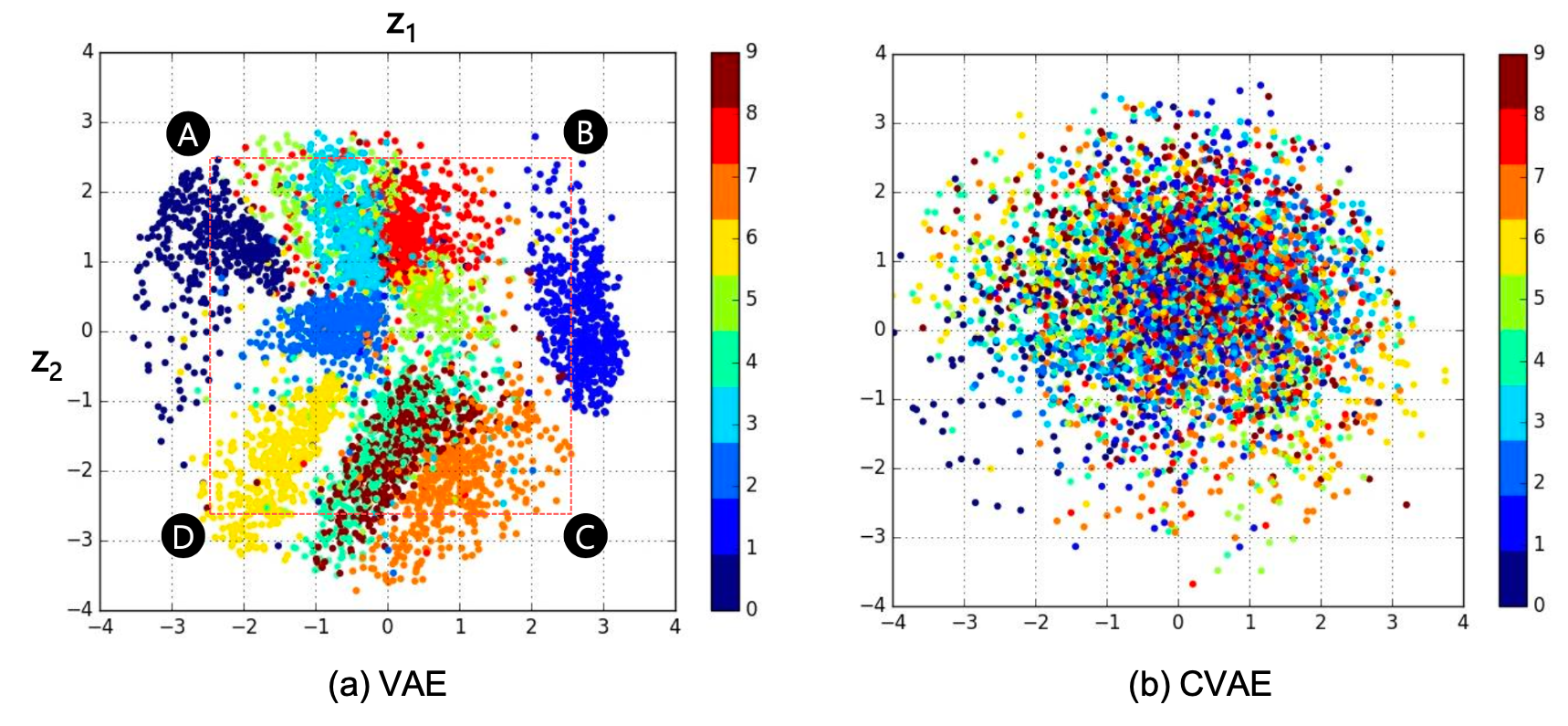 Fig. VAE와 CVAE가 배우는 manifold의 차이
Fig. VAE와 CVAE가 배우는 manifold의 차이
CVAE의 manifold가 굉장히 얽혀 있어 (entangled) 보이지만 사실 condition을 하나씩만 해서 뿌려보면 굉장히 잘 배운 manifold임을 알 수 있습니다.
Beta - Variational AutoEncoder (Beta-VAE)
이번에 알아볼 변이체는 \(\beta\)-VAE입니다.
VAE는 일반적으로 아래와 같은 두 가지 문제점을 가집니다.
- 네트워크가 latent code를 잘 사용하지 않는 (무시한)다 (\(p_{\theta}(x \vert z) \rightarrow p(x)\)). 그 결과 재생한 이미지는 굉장히 흐릿 (blurry) 하다.
- latent code가 압축이 잘 되지 않는다 (\(q_{\phi}(z \vert x)\) very far from \(p(z)\)). 그 결과 네트워크 자체가 identity function처럼 되어 학습시 재생한 이미지는 굉장히 선명하나, 실제로 z로부터 샘플링 해서 디코딩을 할 경우 아무것도 아닌 쓰레기 이미지를 얻게 된다.
이 경우 모두 ELBO의 KLD 텀이 문제인데요,
\[D_{KL} = (q_{\phi}(z \vert x) \parallel p(z))\]전자의 경우 KLD가 너무 작기 때문이고, 후자의 경우 KLD가 너무 크기 때문입니다.
전자의 경우에는 \(q_{phi}(z \vert x)\)에서 x정보를 아예 쓰지 않아 분포 자체가 평균이 0이고 분산이 1인 \(p(z)\)와 같아지게 되고, 따라서 z가 정보를 하나도 가지고 있지 않다는 뜻이며, 그 결과 디코딩을 할 때도 z정보를 하나도 안 쓰게 되는 겁니다.
후자의 경우는 ‘사전 분포인 평균이 0이고 분산인 1인 가우시안 분포를 닮아라’는 정규화 텀 잘 작용하지 않아 z가 너무 많은 정보를 가지고 있다 가 된 것이며, z가 정보가 너무 많기 때문에 원본 이미지를 너무 잘 만들어 내는 것입니다. 그래서 실제로 테스트 타임에서 prior에서 샘플링을 해 condition한 뒤 이미지를 생성하면 디코더가 어쩔 줄 모르게 되는 것이죠.
즉 우리는 이런 VAE의 흔한 문제들을 해결하기 위해서 KLD 텀을 굉장히 신중하게 컨트롤 해야 하는데요, 이를 위해 제안된 것이 바로 beta-VAE 입니다.
beta-VAE의 Objective는 VAE와 별로 차이가 없는데요,
여기서 \(\beta\)는 하이퍼 파라메터로, 문제에 따라서 변경해주면 됩니다.
첫 번쨰 문제가 발생하면 KL을 높혀야 하기 떄문에 \(\beta\)를 작은 값을 곱해주면 되고, 두 번째 문제를 마주치면 반대로 하면 됩니다 (강하게 제약을 거는거죠).
일반적으로 학습 초기에 VAE가 \(z\)에 집중해서 이미지를 reconstruct 하는게 중요하기 때문에 \(beta\)를 학습 초기엔 작은 값으로 하다가 후기에는 큰 값으로 해주는 hyperparameter scheduling을 해주면 됩니다.
Vector Quantized - Variational AutoEncoder (VQ-VAE)
사실 CVAE와 beta-VAE도 VAE에 간단한 아이디어를 추가해서 꽤 흥미롭고 중요한 결과를 냈던 모델들인데요,
양자화 (Vector Quantisation)를 이용한 VQ-VAE가 시사하는 바는 후에 제안되는 다양한 모델들에 지대한 영향력을 끼쳤기 때문에 (생성모델 뿐 아니라 자가 지도 학습 (Self-Supervised Learning, SSL)에도 앞선 모델들보다 더욱 중요한 모델이라고 할 수 있습니다.
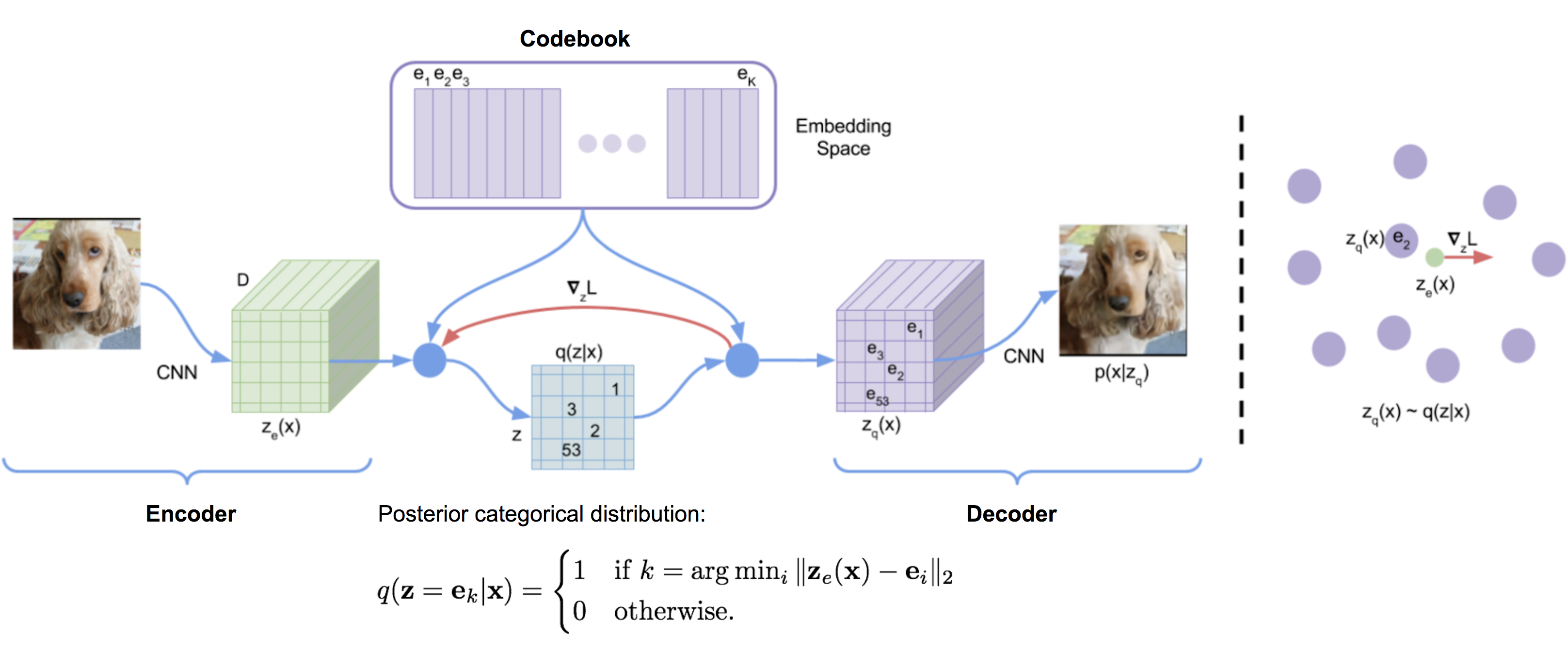 Fig. Model Architecture of Vector Quantized - Variational AutoEncoder (VQ-VAE)
Fig. Model Architecture of Vector Quantized - Variational AutoEncoder (VQ-VAE)
논문에 따르면 VQ-VAE가 VAE와 크게 다른점은 두 가지라고 하는데요,
- Encoder의 출력을 discrete하게 했다. (VAE는 continuous 였죠? 예를들면 2차원 가우시안 분포상의 어느 점이던 가능했습니다.) 양자화를 함으로써 VAE의 흔한 문제점 (z 정보를 안쓴다는 것)이라고 지적되었던 “posterior collapse” 문제를 해결할 수 있었다.
- Prior가 고정되어 (static) 있지 않고 학습된다 (learnt).
이 결과 VQ-VAE는 Speech, Video Generation 등의 task에서 좋은 퀄리티를 보였다고 합니다.
천천히 VQ-VAE가 어떻게 작동하는지 살펴보자면, 우선 VAE처럼 (\(x \rightarrow z\)), (\(z \rightarrow x\)) 두 가지를 학습하는건 맞지만, 여기서 \(z\)를 양자화 하는 과정을 추가되었고 이 과정이 논문에 아래 그림으로 나타나 있습니다.
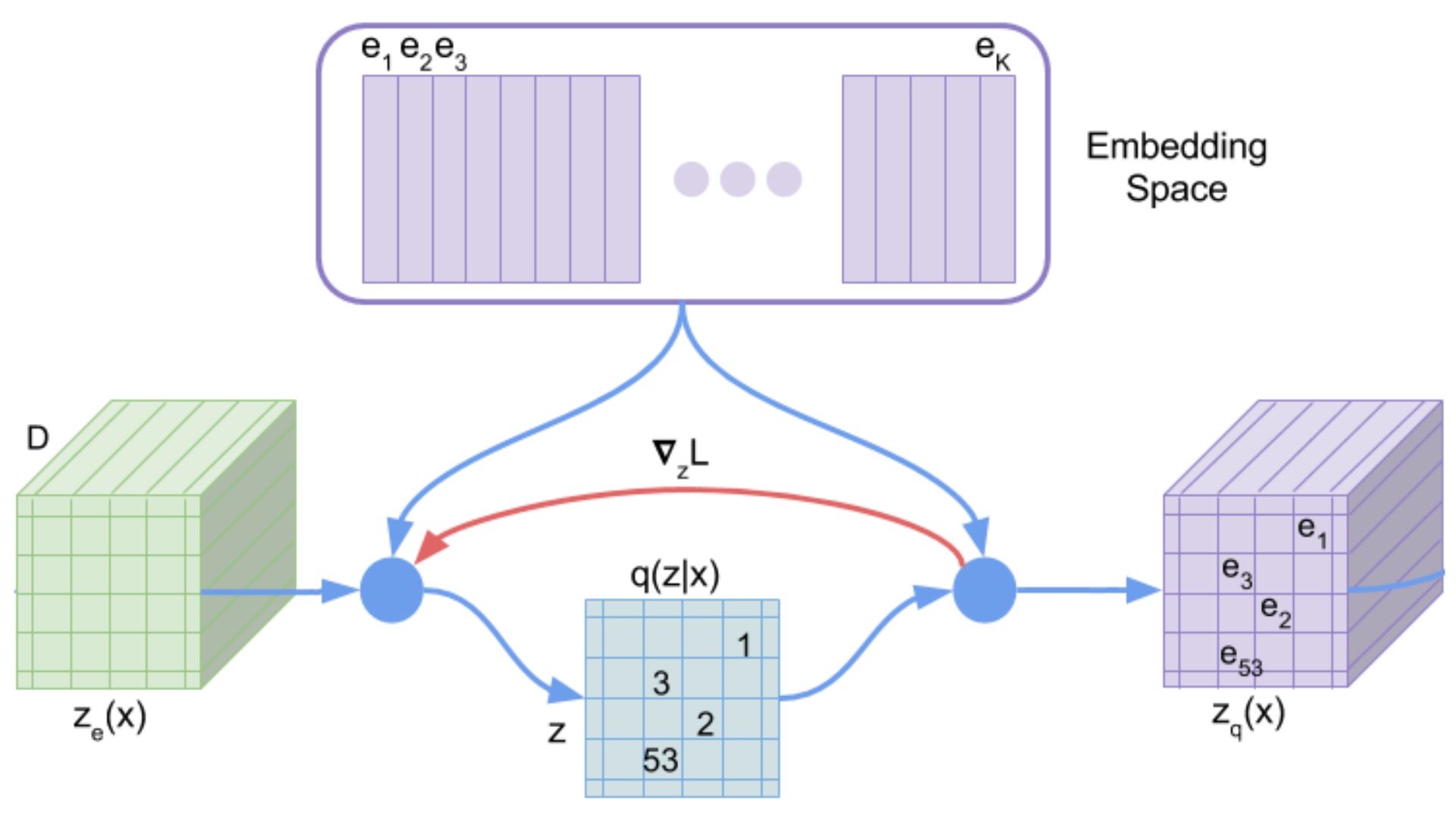 Fig.
Fig.
최종적으로 우리가 원하는 것은 VAE와 다르게 Discrete Latent Space를 배우는 것입니다.
Objective Function
먼저 간단한게 Notation을 아래처럼 정의하고
- Input (image) : \(x\)
Encoder output: \(z_e(x)\)- Latent Embedding Space : \(e \in R^{K \times D}\)
- Size of the Discrete Latent Space (i.e. K-way Categorical) : \(K\)
- Latent Embedding Vector : \(e_i \in R^D\)
- The Dimensionality of each Latent Embedding Vector : \(D\)
- Latent Variable : \(z\)
Decoder Input: \(z_q(x) = e_k\)
VAE에서 중요한 아래 세가지가 요소들에 대해서 생각을 해보도록 하겠습니다.
- approximate posterior : \(q(z \vert x)\)
- prior : \(p(z)\)
- likelihood : \(p(x \vert z)\)
여기서 먼저 approximate posterior를 아래처럼 정의할 수 있는데,
\[q(z = k \vert x) = \left\{\begin{matrix} 1 \text{ for } k = argmin_j \| z_e(x) - e_j \|_2, \\ 0 \text{ otherwise} \end{matrix}\right.\]우리는 이산적인 \(z\) 분포를 배우고 싶기 때문에, 이 근사 분포는 연속적인 분포가 아니라 이산적인 분포, 즉 Categorical Distribution을 가정할 수 있습니다.
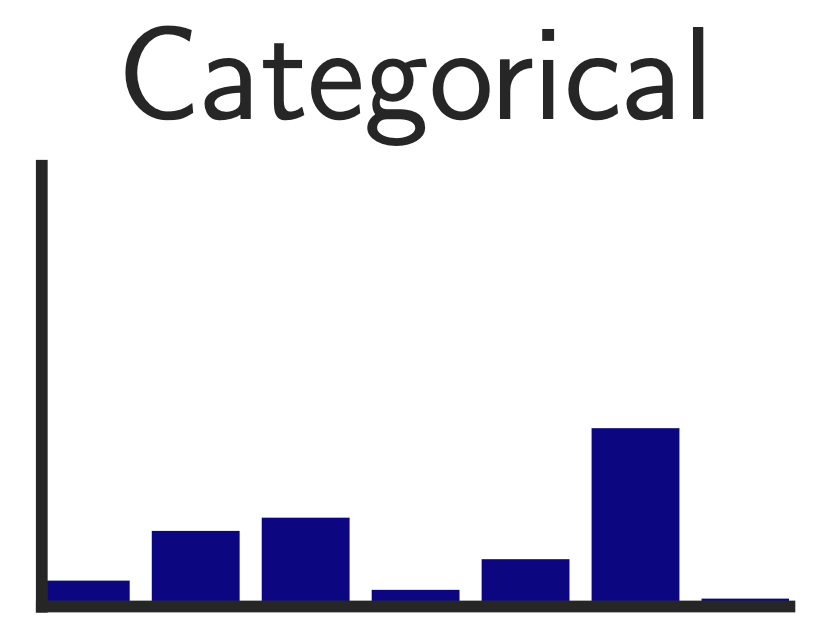 Fig. Categorical Distribution
Fig. Categorical Distribution
수식에 따르면 \(q(z \vert x)\)는 인코더 출력 \(z_e(x)\)와 가장 가까운 거리 (L2-norm, 즉 Euclidean Distance로 비교)에 있는 임베딩 벡터 \(e_k\)만 1이고 나머지는 다 0인 One-hot 분포가 됩니다.
 Fig. One-hot Categorical Distribution
Fig. One-hot Categorical Distribution
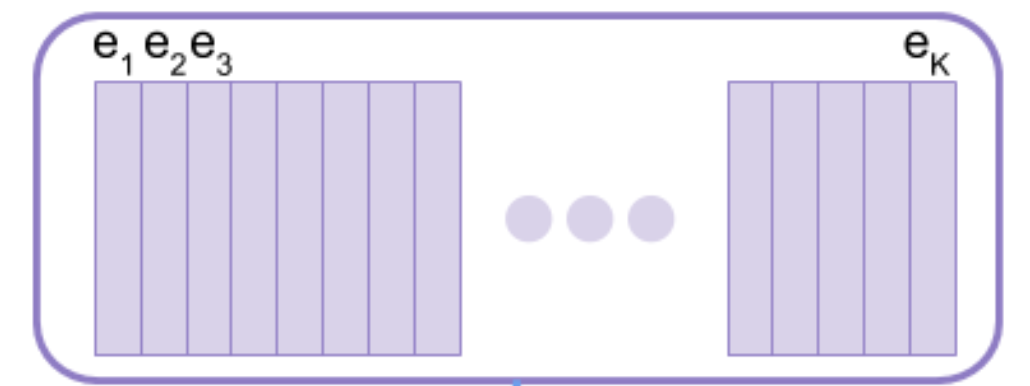 Fig. 임베딩 스페이스에 존재하는 각각의 임베딩 벡터들, 각각의 벡터들, \(e_1, e_2, \cdots\)와 \(z_e(x)\)간의 거리를 재서 선택한다.
Fig. 임베딩 스페이스에 존재하는 각각의 임베딩 벡터들, 각각의 벡터들, \(e_1, e_2, \cdots\)와 \(z_e(x)\)간의 거리를 재서 선택한다.
여기서 거리가 가장 가까운 벡터를 선택하여 인코더의 최종 출력이라고 생각하고, 디코더로 넘겨주며 이 디코더를 통해서 원본 데이터를 재생 (Reconstruction) 합니다.
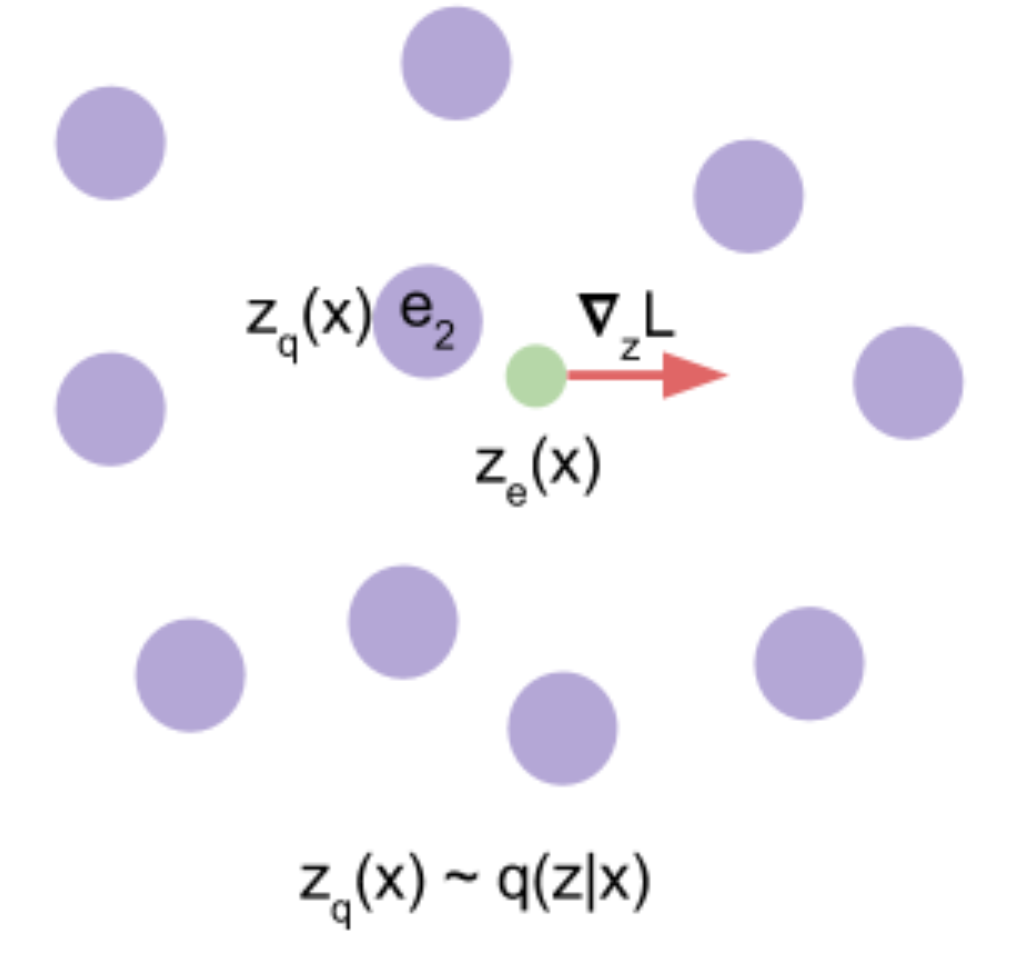 Fig. 그림에서 \(z_e(x)\)와 가장 가까운 임베딩 벡터는 \(e_2\)이며, 이 벡터가 곧 \(z_q(x)\)이 된다.
Fig. 그림에서 \(z_e(x)\)와 가장 가까운 임베딩 벡터는 \(e_2\)이며, 이 벡터가 곧 \(z_q(x)\)이 된다.
그리고 사전 분포 \(p(z)\)를 VAE와 마찬가지로 넓게 분포된 이산 분포를 원하기 때문에 Uniform Distribution 을 고르게 됩니다.
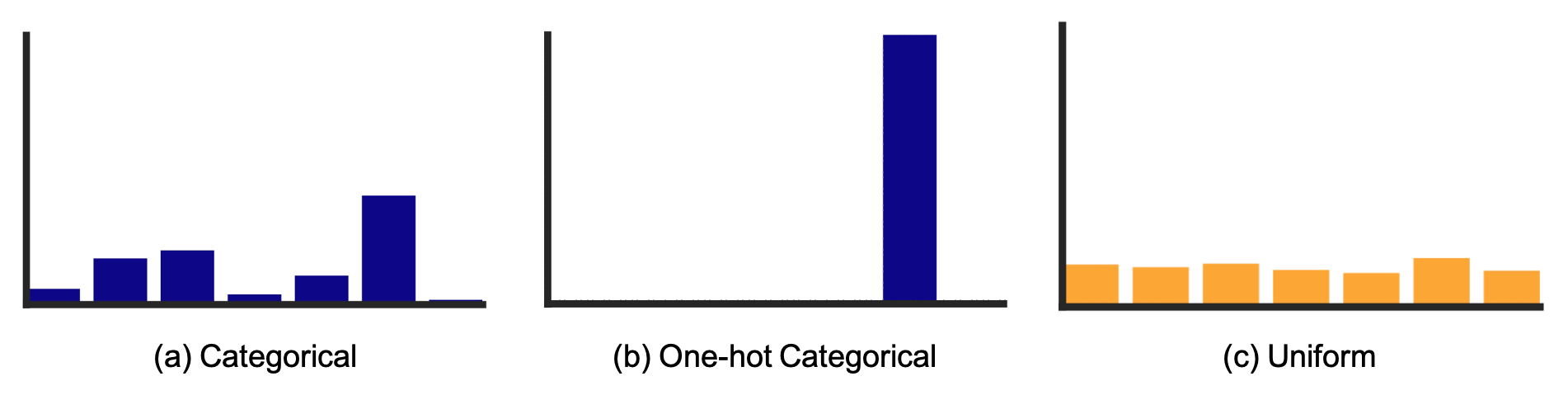 Fig. 사실 그림에서 Uniform Distribution이 Categorical Distribution의 엔트로피가 최대버전인 것은 아닙니다.
Fig. 사실 그림에서 Uniform Distribution이 Categorical Distribution의 엔트로피가 최대버전인 것은 아닙니다.
- approximate posterior : \(q(z \vert x)\) \(\leftarrow\)
One-hot Categorical Distribution - prior : \(p(z)\) \(\leftarrow\)
Uniform Distribution - likelihood : \(p(x \vert z)\) \(\leftarrow\) (Gaussian Distribution일 경우 Reconstruction Error는 MSE가 됨)
이제 최종 Objective를 구하면 아래와 같게 되는데,
\[L = \underbrace{log p(x \vert z_q(x))}_{\textrm{reconstruction loss}} + \underbrace{\| sg[z_e(x)] - e \|_2^2}_{\textrm{VQ loss}} + \underbrace{\beta \| z_e(x) - sg[e] \|_2^2}_{\textrm{commitment loss}}\]여기서 디코더의 출력분포가 가우시안 분포라면 Negative Log Likelihood는 MSE loss가 되므로 아래와 같은 수식을 얻을 수 있습니다.
여기서 \(\text{sq}[.]\) 는 stop_gradient 연산자 (operator)를 의미하며, 이 연산자가 하는 일은 입력값을 네트워크에 forwarding 할 때는 identity function처럼 연산해주고 backwarding, 즉 역전파를 할 때는 gradient가 흐르는것을 막아줍니다.
즉, 피연산자 (operand)가 업데이트 되지 않도록 해주는 거죠.
- Decoder는
첫 번째 term만을 최적화 하며, 두 번째, 세 번째 term은 쓰지 않습니다. - Encoder는
첫 번째와 마지막 term을 최적화 합니다. - Discrete Space Embedding을 담당하는 Codebook은
두 번째 term만 사용합니다.
여기서 두, 세번째 term이 존재하는 이유는, 인코더의 출력 벡터를 양자화 할 때 사용된 argmin opertaor때문에 gradient가 앞으로 흐르지 않게 되고, 이에 따라서 양자화를 담당하는 임베딩 벡터들을 모아둔 Codebook이 학습되지 않기 때문입니다. 따라서 두 번째 loss term은 \(z_e(x)\)는 가만히 있고 \(e_k\) 벡터가 \(z_e(x)\)와 가까워지도록 움직이는 것이고, 세 번째 loss term은 \(z_e(x)\)가 \(e_k\)쪽으로 움직이게 되는 것입니다.
 Fig. 빨간색 선으로 표시된 \(\bigtriangledown_z L\)에 따라서 인코더가 출력 벡터값을 바꾸도록 학습된다.
Fig. 빨간색 선으로 표시된 \(\bigtriangledown_z L\)에 따라서 인코더가 출력 벡터값을 바꾸도록 학습된다.
그리고 모든 VAE의 Obejctive인 ELBO에 등장하는 KLD term은 우리가 uniform prior를 가정했기 때문에 상수가 돼 사라진다고 합니다.
VQ-VAE는 Discrete Latent Space를 학습하는 것 이외에도 Test time에서 사용되는 Prior를 Autoregressive하게 만들거나 디코더를 Autoregressive하게 만들어서 좋은 결과를 얻어내기도 했습니다.
즉 Test time에 \(p(z)\) 분포로 부터 \(z\) 벡터를 한 번 샘플링하고 이를 바탕으로 \(p(x \vert z)\)를 만들어내는 것이 기존 VAE방식이었는데, 이럴 경우 이미지 각각의 픽셀이 서로 영향을 주지 않고 독립적으로 만들어 지는 것이기 때문에 이것이 문제가 있다고 생각하여, Autoregressive하게 픽셀을 하나씩 만들거나 만들 때 마다 prior로부터 이전 \(z\) 벡터들을 given으로한 새로운 \(z\)를 계속 샘플링해서 given으로 주는겁니다.
Autoregressive Models
Autoregressive (AR) Model이 무엇인지 잘 와닿지 않는 분들이 계실까봐 준비를 해봤는데요, 이는 아래와 같이 이미지의 픽셀을 하나씩 만들어 내는데 매 픽셀을 만들어낼 때 마다 이전까지 만들어졌던 픽셀을 given으로 만들어낸다는 특징을 가지고 있는 모델입니다.
 Fig. 이미지를 픽셀을 Autoregressive하게 만들어내는 과정.
Fig. 이미지를 픽셀을 Autoregressive하게 만들어내는 과정.
AR Model은 \(x_1\)이 주어지고, \(x_2\)를 만들 때는 \(p(x_2 \vert x_1)\)로 만들어내고 … 를 반복하면서 픽셀들을 하나씩 만들고, 이를 원본 픽셀들과 비교해서 학습하는 것으로 이를 수식으로 나타내면 아래와 같습니다.
\[\begin{aligned} & p(x_1) = p(x_1) & \\ & p(x_2) = p(x_2 \vert x_1) p(x_1) & \\ & p(x_3) = p(x_3 \vert x_2,x_1) p(x_2 \vert x_1) p(x_1) & \\ & \vdots & \\ & p(x) = \prod_{i=1}^{n^2} p(x_i \vert x_1, \cdots, x_{i-1}) & \\ \end{aligned}\]이렇게 만들어진 최종 likelihood \(p(x)\)를 최대화 하면 되는 것이죠 (= 각 정답 픽셀들과의 loss를 최소화).
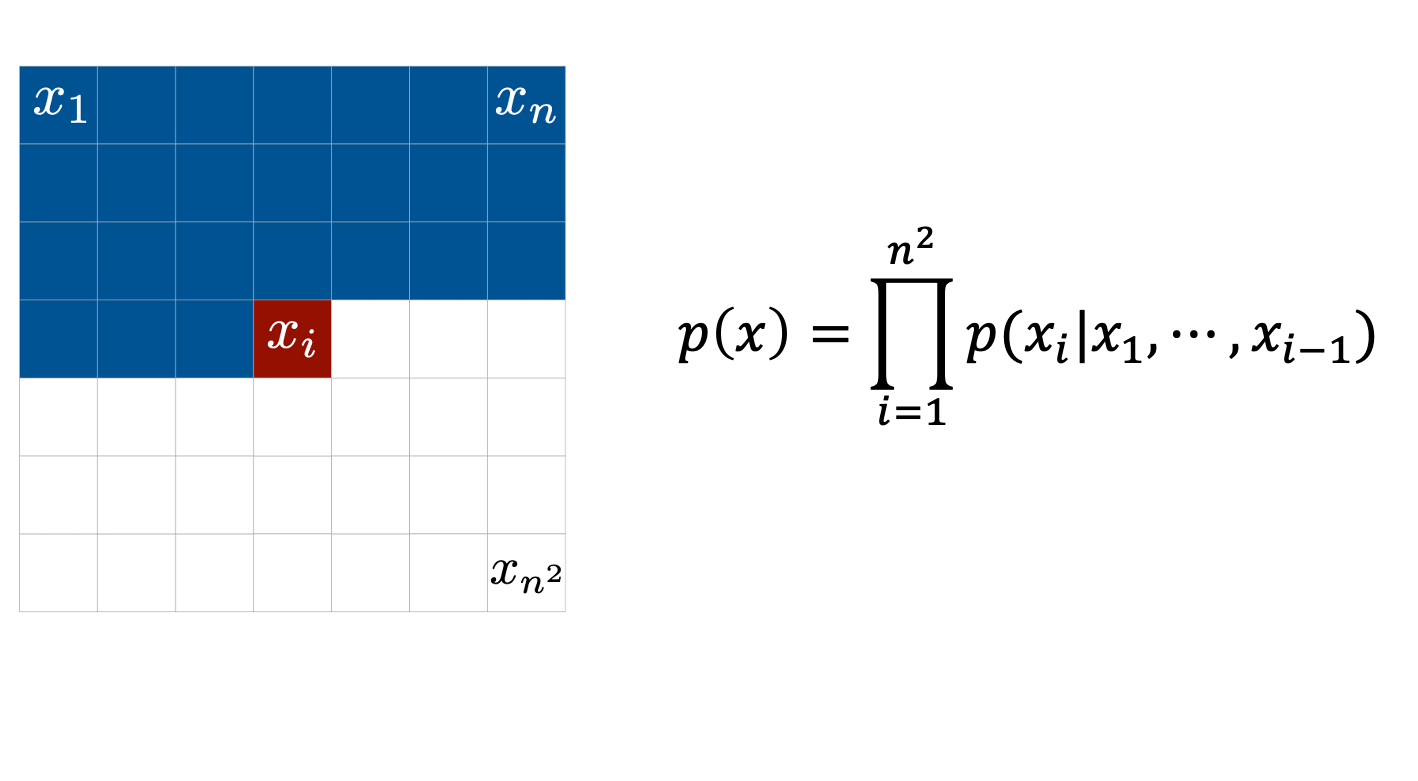
각각의 조건부 확률 (Conditional Probability)을 모델링 하는 모듈로 원하는 NN을 쓰면 됩니다 (RNN이 일반적).
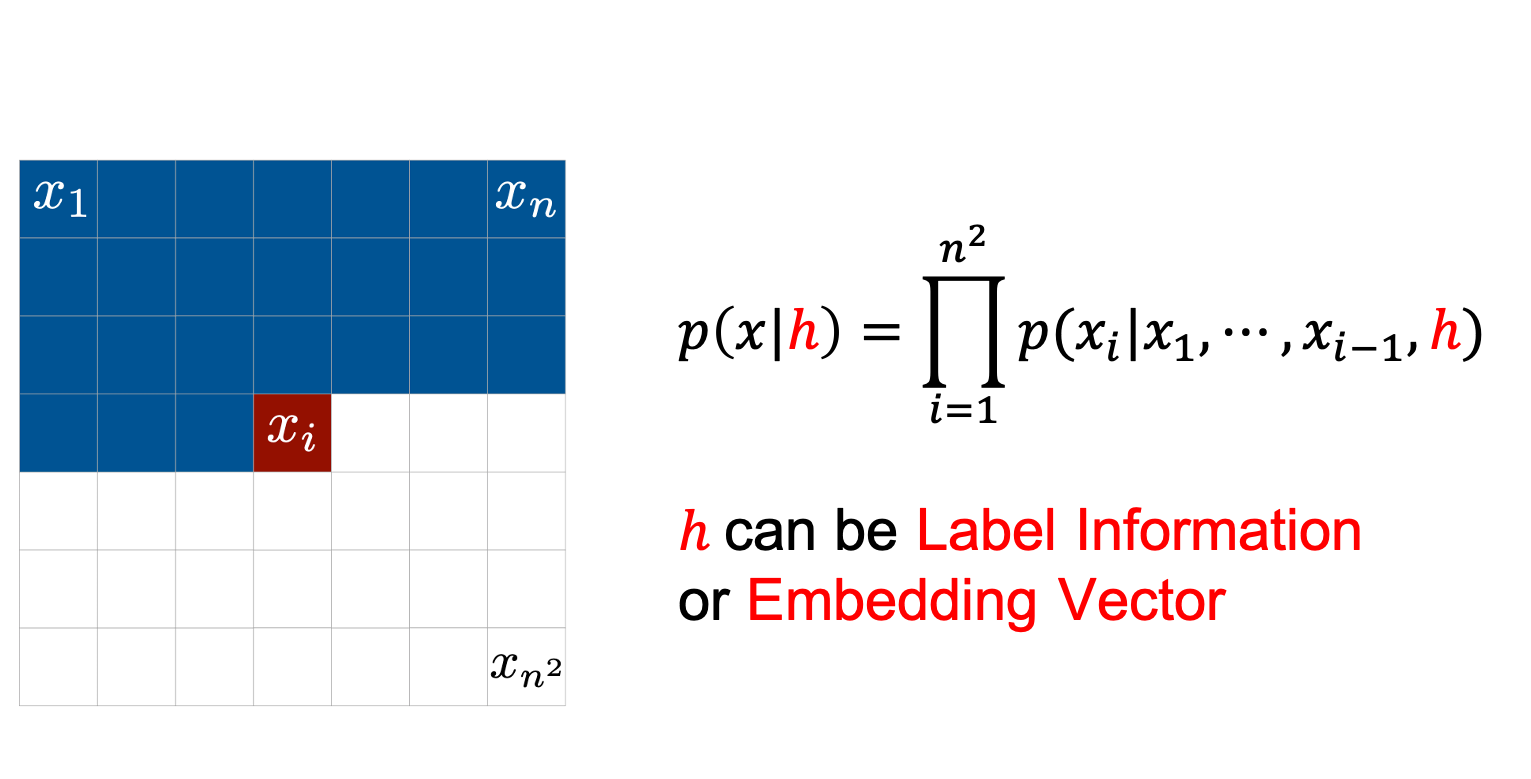
또한 이런 AR Model에 다양한 정보를 condition해서 학습 및 샘플 생성을 할 수 있는데요, 예를 들어 <이미지, 정답> pair중 정답 벡터 (i.e. \(h=[0,0,1,0,\cdots,0]\))를 condition으로 주고 학습했다면 나중에 원하는 label을 컨디션으로 줘서 (i.e. 고양이) 해당 이미지를 만들어 낼 수도 있습니다.
PixelCNN for Image and Video
이러한 AR Model을 이미지 쪽에 잘 적용하기 위해서, Computer Vision task에서 굉장히 잘 작용하는 CNN을 도입한 모델이 바로 PixelCNN 이며,
![]() Fig. Vanilla AR Model VS PixelCNN
Fig. Vanilla AR Model VS PixelCNN
VQ-VAE 논문에서는 이미지, 영상 쪽 실험을 할 때 디코더나 prior에 Autoregressive한 모델링을 섞어줄 때 바로 이 PixelCNN을 사용했습니다.
WaveNet for Audio
또한 음성 데이터를 다루기 위한 AR Model로 논문에서는 WaveNet을 사용했는데요,
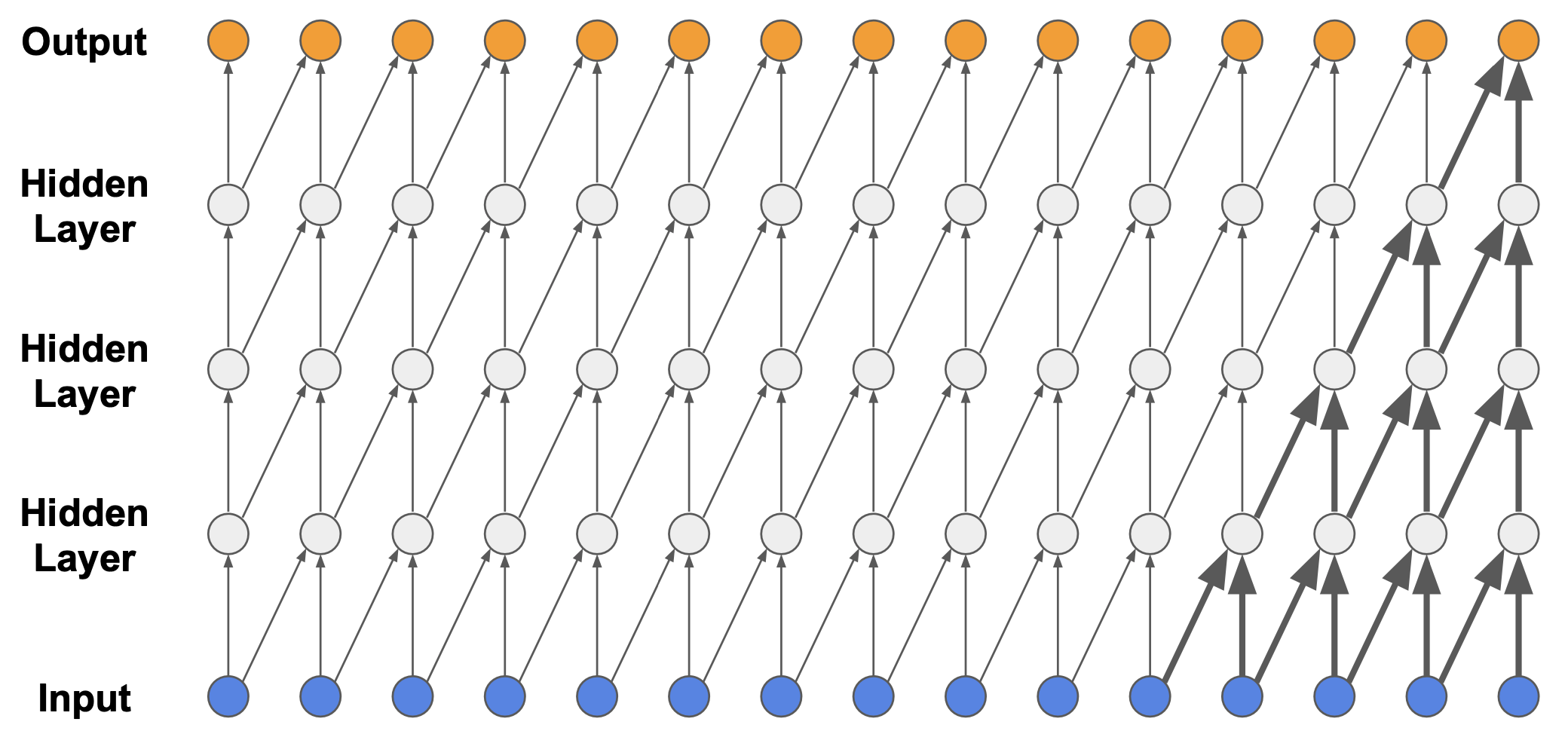 Fig. 심플한 AR Model을 Audio에 적용했을 때의 단점
Fig. 심플한 AR Model을 Audio에 적용했을 때의 단점
WaveNet은 일반적으로 굉장히 샘플 수가 많은 음성에 대해서 Autoregressive하게 벡터를 만들어 내는데 사용되는 샘플 수가 굉장히 적다는 단점을 보완하기 위해서 (물론 층을 깊게 쌓으면 굉장히 많은 샘플을 given으로 만들어 낼 수 있겠죠? 하지만 그렇게 깊게 레이어를 쌓는거는 계산상 불가능에 가깝습니다.) 제안된 방법론 입니다.
(예를 들어 음성이 4초인데, sampling rate이 16000 이라면 샘플 벡터 수가 64000입니다.)
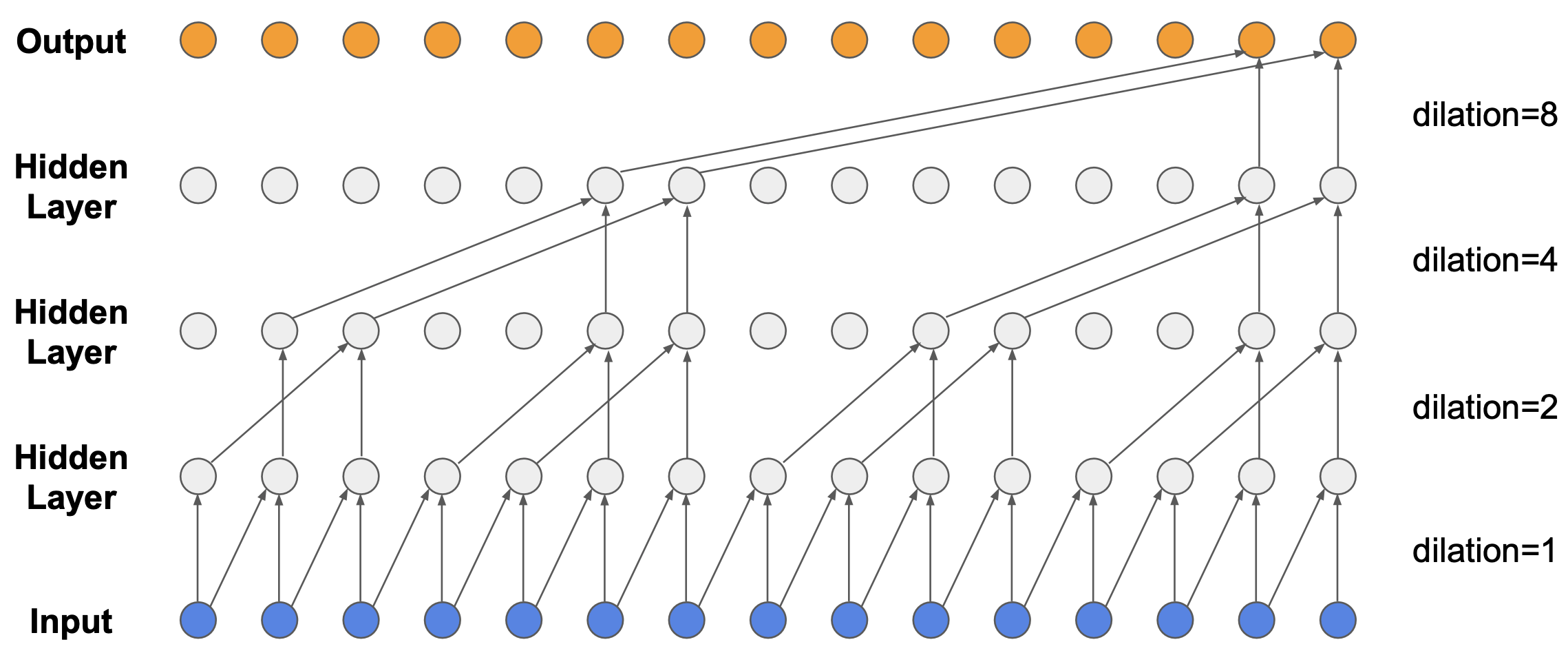 Fig. WaveNet은 Dilated Convolution 기법을 사용해서 Receptive Field가 적다는 단점을 커버했다.
Fig. WaveNet은 Dilated Convolution 기법을 사용해서 Receptive Field가 적다는 단점을 커버했다.
WaveNet은 심플하게 얘기하자면 위의 그림처럼 Dilated 1D Convolution Layer를 사용해서 넓게 보고 (Receptive Field를 증가시킴) Autoregressive하게 토큰을 만들어 내겠다는 겁니다.
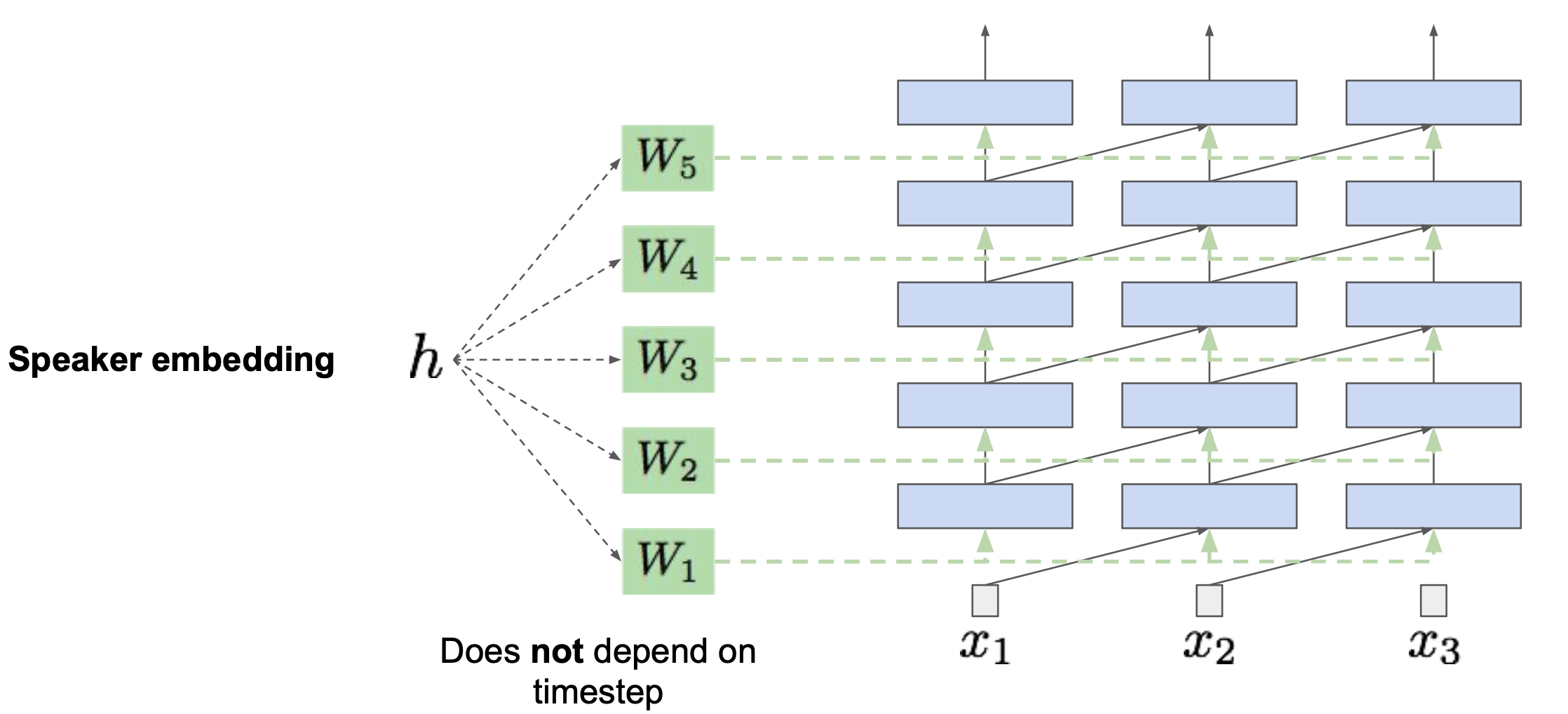 Fig. Conditional WaveNet
Fig. Conditional WaveNet
일반적으로 학습한 WaveNet을 통해 생성한 음성이 웅얼거리는 듯한 (mumble) 단점이 있기 때문에, 앞서 말한 것 처럼 화자 정보 (Speaker Embedding)나 문장 (Text)을 조건부로 주고 학습하면 우리가 원하는 음성을 생성해 낼 수 있습니다.
Autoregressive Models as Decoder
이러한 AR Model을 AE의 디코더 부분에 사용할 수 있는데요, 그 말인 즉 latent variable을 이용해서 원본 이미지 픽셀들을 independent하게 만들어내는 일반적인 AE, VAE의 단점을 보완하겠다는 겁니다.
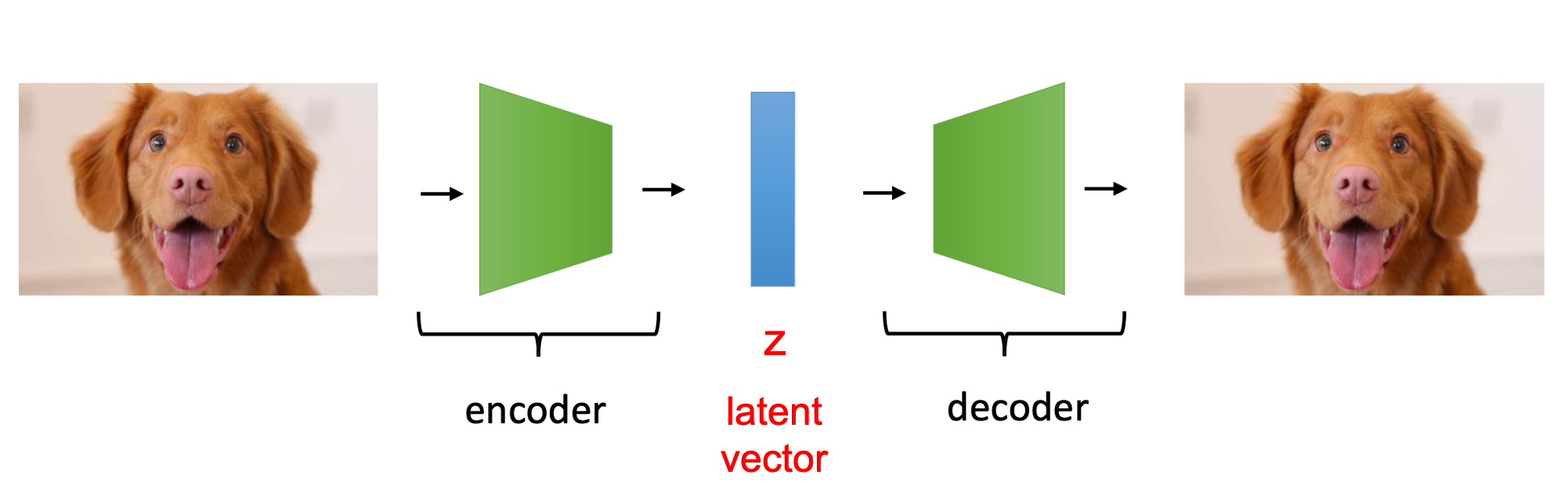 Fig. 일반적인 AE, VAE는 픽셀들을 복원할 때 독립 가정 (Independence Assumption)을 하고 만든다.
Fig. 일반적인 AE, VAE는 픽셀들을 복원할 때 독립 가정 (Independence Assumption)을 하고 만든다.
즉 \(p(x \vert z)\) 를 아래와 같이 만든다는 겁니다.
\[p(x \vert z) = \prod_{i} p(x_i \vert x_1,\cdots,x_{i-1},z)\]![]() Fig. Decoder를 AR Model로 만들면 더욱 잘 이미지를 복원할 수 있다.
Fig. Decoder를 AR Model로 만들면 더욱 잘 이미지를 복원할 수 있다.
이를 VAE나 VQ-VAE로 확장하면
\[\begin{aligned} & L_{VAE} = - \sum_{i=1}^{N} [ log p(x_i \vert z ) - D_{KL} ( q(z \vert x_i ) \parallel p(z) ) ] & \\ & L_{VQ-VAE} = \underbrace{log p(x \vert z_q(x))}_{\textrm{reconstruction loss}} + \underbrace{\| sg[z_e(x)] - e \|_2^2}_{\textrm{VQ loss}} + \underbrace{\beta \| z_e(x) - sg[e] \|_2^2}_{\textrm{commitment loss}} & \end{aligned}\]아래와 같이 쓸 수 있겠죠.
\[\begin{aligned} & L_{VAE} = - \sum_{i=1}^{N} [ log \prod_{i} p(x_i \vert x_1,\cdots,x_{i-1},z) - D_{KL} ( q (z \vert x_i ) \parallel p(z) ) ] & \\ & L_{VQ-VAE} = \underbrace{log \prod_{i} p(x_i \vert x_1,\cdots,x_{i-1},z)}_{\textrm{reconstruction loss}} + \underbrace{\| sg[z_e(x)] - e \|_2^2}_{\textrm{VQ loss}} + \underbrace{\beta \| z_e(x) - sg[e] \|_2^2}_{\textrm{commitment loss}} & \end{aligned}\]이렇게 함으로써 latent variable, \(z\)는 더욱 다양하고 의미있는 정보를 배우게 될 것이라는게 이 방법론을 제안한 저자들의 주장인데요,
실제로 AE와 PixelCNN을 디코더로 쓴 AE가 각각 테스트 이미지를 입력받아 차원을 줄인 후 복원한 결과를 보면 PixelCNN을 디코더로 사용한 결과가 더 선명하고 다양한 것을 알 수 있습니다.
![]() Fig. AE vs AE with PixelCNN Decoder
Fig. AE vs AE with PixelCNN Decoder
이러한 방법론을 이용해서 VQ-VAE를 제안한 논문에서도 이미지, 영상, 음성에 대해서 아래와 같이 AR Model을 디코더로 사용해 모델링 하기도 했습니다.
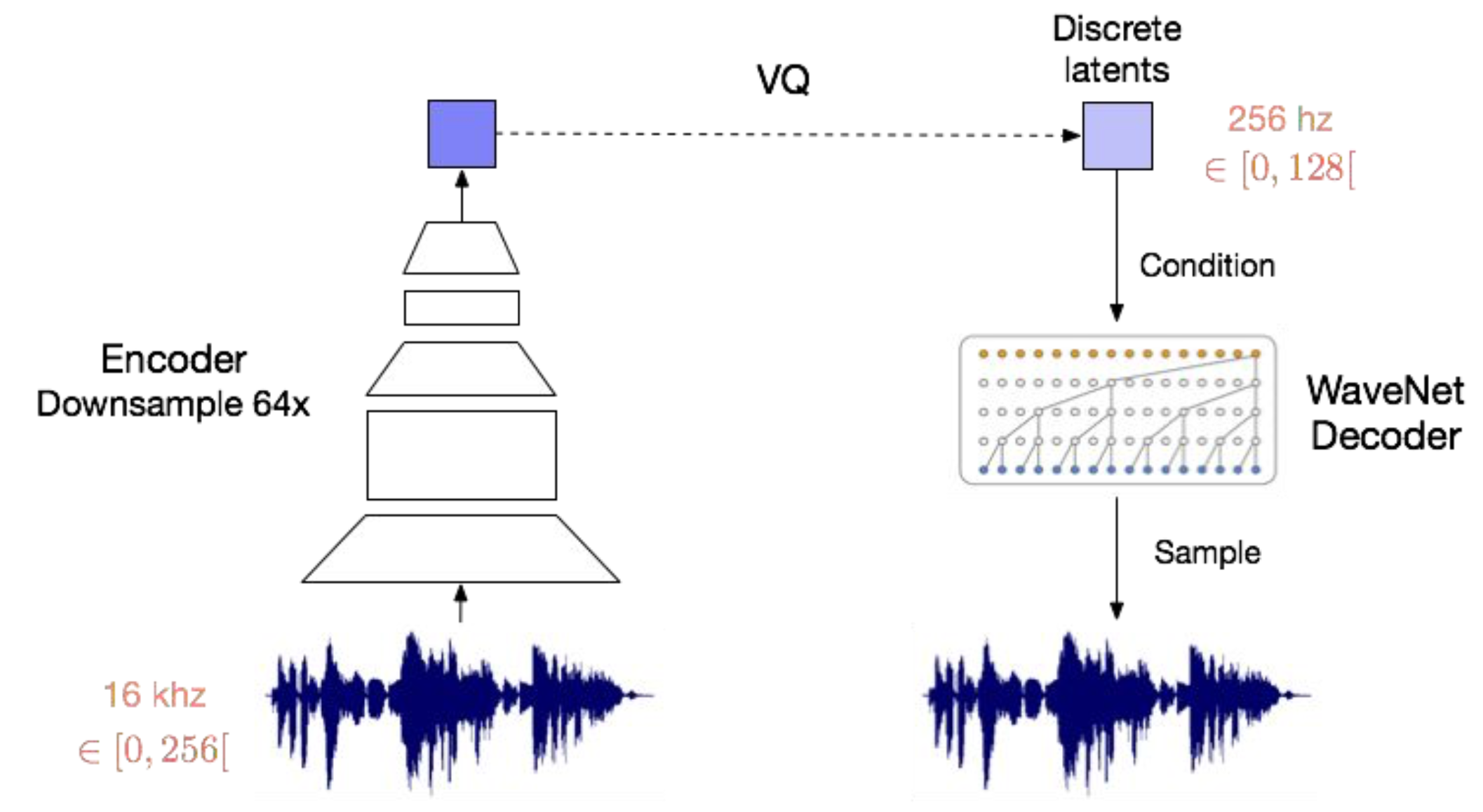 Fig. WaveNet을 디코더로 사용한 경우
Fig. WaveNet을 디코더로 사용한 경우
Autoregressive Prior
한편 AR Model을 prior에 적용하는 방법도 있는데요, 이는 아래의 PixelVAE의 논문의 그림과 수식을 참고하면 좋을 것 같아서 한 번 가져와 봤습니다.
![]() Fig. PixelVAE. Authors use PixelCNN to model an autoregressive decoder and autoregressive prior for a VAE.
Fig. PixelVAE. Authors use PixelCNN to model an autoregressive decoder and autoregressive prior for a VAE.
VQ-VAE가 VAE와 비교해서 크게 다르지 않기 때문에 VAE에 대해서 어떻게 Autoregressive prior를 적용했는지 알아보도록 하겠습니다.
- VAE
- approximate posterior : \(q(z \vert x)\)
- prior : \(p(z)\)
- likelihood : \(p(x \vert z)\)
- VAE with
Autoregressive Decoder- approximate posterior : \(q(z \vert x)\)
- prior : \(p(z)\)
- likelihood : \(p(x \vert z) = \prod_i p(x_i \vert x_1, \cdots, x_{i-1},z)\)
- VAE with Autoregressive Decoder and
Autoregressive Prior- approximate posterior : \(q(z_1,\cdots,z_L) = q(z_1 \vert x) \cdots q(z_L \vert x)\)
- prior : \(p(z_1,\cdots,z_L) = p(z_L)p(z_{L-1} \vert z_L) \cdots p(z_1 \vert z_2)\)
- likelihood : \(p(x \vert z) = \prod_i p(x_i \vert x_1, \cdots, x_{i-1},z)\)
![]() Fig. VAE와 함께 prior sampling을 위한 Autoregressive Model이 학습되는 과정
Fig. VAE와 함께 prior sampling을 위한 Autoregressive Model이 학습되는 과정
이를 적용하면 우리는 VAE의 Objective를 아래와 같이 수정할 수 있습니다.
- VAE
- \[- L(x,q,p) = -\mathbb{E}_{z \sim q(z \vert x)} log p(x_i \vert z ) + D_{KL} ( q(z \vert x_i ) \parallel p(z) )\]
- VAE with
Autoregressive Decoder- \[- L(x,q,p) = -\mathbb{E}_{z \sim q(z \vert x)} \prod_i p(x_i \vert x_1, \cdots, x_{i-1},z) + D_{KL} ( q(z \vert x_i ) \parallel p(z) )\]
- VAE with Autoregressive Decoder and
Autoregressive Prior- \[\begin{aligned} & - L(x,q,p) = -\mathbb{E}_{z_1 \sim q(z_1 \vert x)} \prod_i p(x_i \vert x_1, \cdots, x_{i-1},z_1) + D_{KL} ( q(z_1,\cdots,z_L \vert x) \parallel p(z_1,\cdots,z_L) ) & \\ & = -\mathbb{E}_{z_1 \sim q(z_1 \vert x)} \prod_i p(x_i \vert x_1, \cdots, x_{i-1},z_1) + \int_{z_1, \cdots, z_L} \prod_{j=1}^L q(z_j \vert x) \sum_{i=1}^L log \frac{q(z_i \vert x)}{p(z_i \vert z_{i+1})} dz_1 \cdots dz_L & \\ & = -\mathbb{E}_{z_1 \sim q(z_1 \vert x)} \prod_i p(x_i \vert x_1, \cdots, x_{i-1},z_1) + \sum_{i=1}^L \int_{z_1, \cdots, z_L} \prod_{j=1}^L q(z_j \vert x) log \frac{q(z_i \vert x)}{p(z_i \vert z_{i+1})} dz_1 \cdots dz_L & \\ & = -\mathbb{E}_{z_1 \sim q(z_1 \vert x)} \prod_i p(x_i \vert x_1, \cdots, x_{i-1},z_1) + \sum_{i=1}^L \int_{z_i, z_{i+1}} q(z_{i+1} \vert x) q(z_i \vert x) log \frac{q(z_i \vert x)}{p(z_i \vert z_{i+1})} dz_i dz_{i+1} & \\ & = -\mathbb{E}_{z_1 \sim q(z_1 \vert x)} \prod_i p(x_i \vert x_1, \cdots, x_{i-1},z_1) + \sum_{i=1}^L \mathbb{E}_{z_{i+1} \sim q(z_{i+1} \vert x)} [ D_{KL} ( q(z_i \vert x) \parallel p(z_i \vert z_{i+1}) ) ] & \\ \end{aligned}\]
사실은 VQ-VAE 논문에 정확한 수식이 기재되어 있지 않아서
VQ-VAE에서는 어떤 방식으로 Autoregressive Prior, Decoder를 사용했는지
정확하게 알 수는 없지만 위와 유사한 방법으로 적용됐을 거라고 생각하시면 될 것 같고
나중에 궁금하신 분들은 구현 코드나 논문을 추가적으로 보시면 좋을 것 같습니다.
추가적으로 이 부분은 제가 논문을 읽으면서 맨처음에 잘 상상이 가지 않았던 부분인데요, 우리가 앞서 정의한 VQ-VAE loss는 discrete latent vector 하나만을 생각해서 이에 대해 K개의 임베딩 벡터중 하나와 매핑되는 것이었지만, 실제 실험에 사용된 것은 ImageNet의 경우 \(32 \times 32 \times 1\) (1채널에 \(32 \times 32 = 1024\)개의 벡터가 있는 것) 이었다는 것을 아셔야 합니다.
그러니까 Loss를 실제로 구현할 때는 각각의 Latent Vector들에 대해서 다 적용되어야 하는 것이죠.
VQ-VAE 논문에서는 학습 시에는 prior를 constant and uniform Categorical Distribution으로 유지하면서 학습하고,
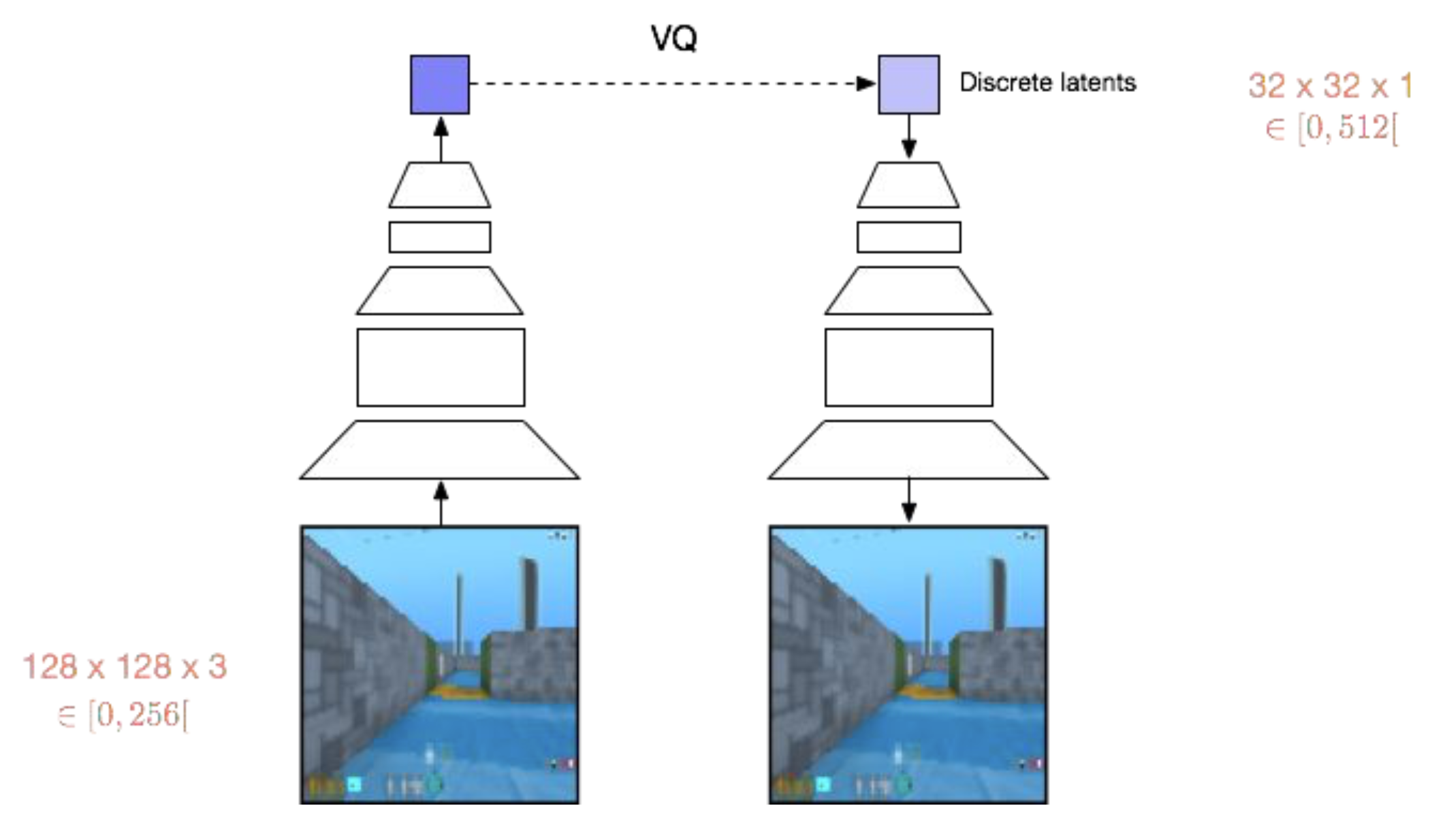 Fig. 학습 시에는 prior를 고정하고 VQ-VAE를 학습한다. 총 \(32 \times 32 \times 1 = 1024\) 개의 양자화된 벡터를 이용해 학습한다.
Fig. 학습 시에는 prior를 고정하고 VQ-VAE를 학습한다. 총 \(32 \times 32 \times 1 = 1024\) 개의 양자화된 벡터를 이용해 학습한다.
Test Time, 즉, 추론 시에는 당연히 여러개의 (지금은 \(1024\)) 이산적인 샘플 (discrete sample)을 독립적으로 샘플링 해서 사용할 수도 있고, 처음 \(z_1\)을 뽑고, \(z_1\)을 통해 \(z_2\)를 뽑고… 이런식으로 반복해서 서로 독립적이지 않은 연관된 샘플 시퀀스를 뽑을 수 있습니다.
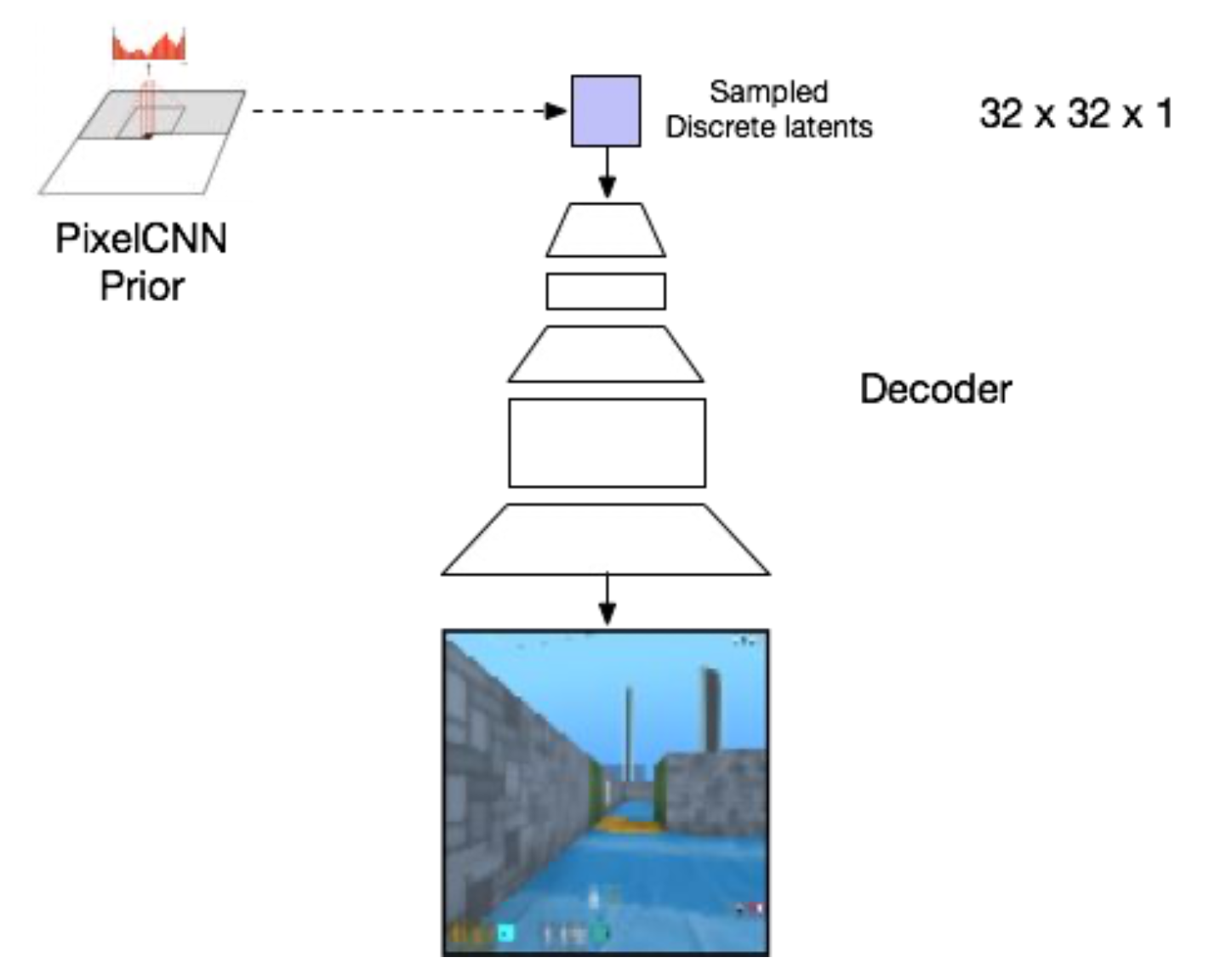 Fig. Prior Sample Vector들을 Autoregressive하게 만들어서 사용한다.
Fig. Prior Sample Vector들을 Autoregressive하게 만들어서 사용한다.
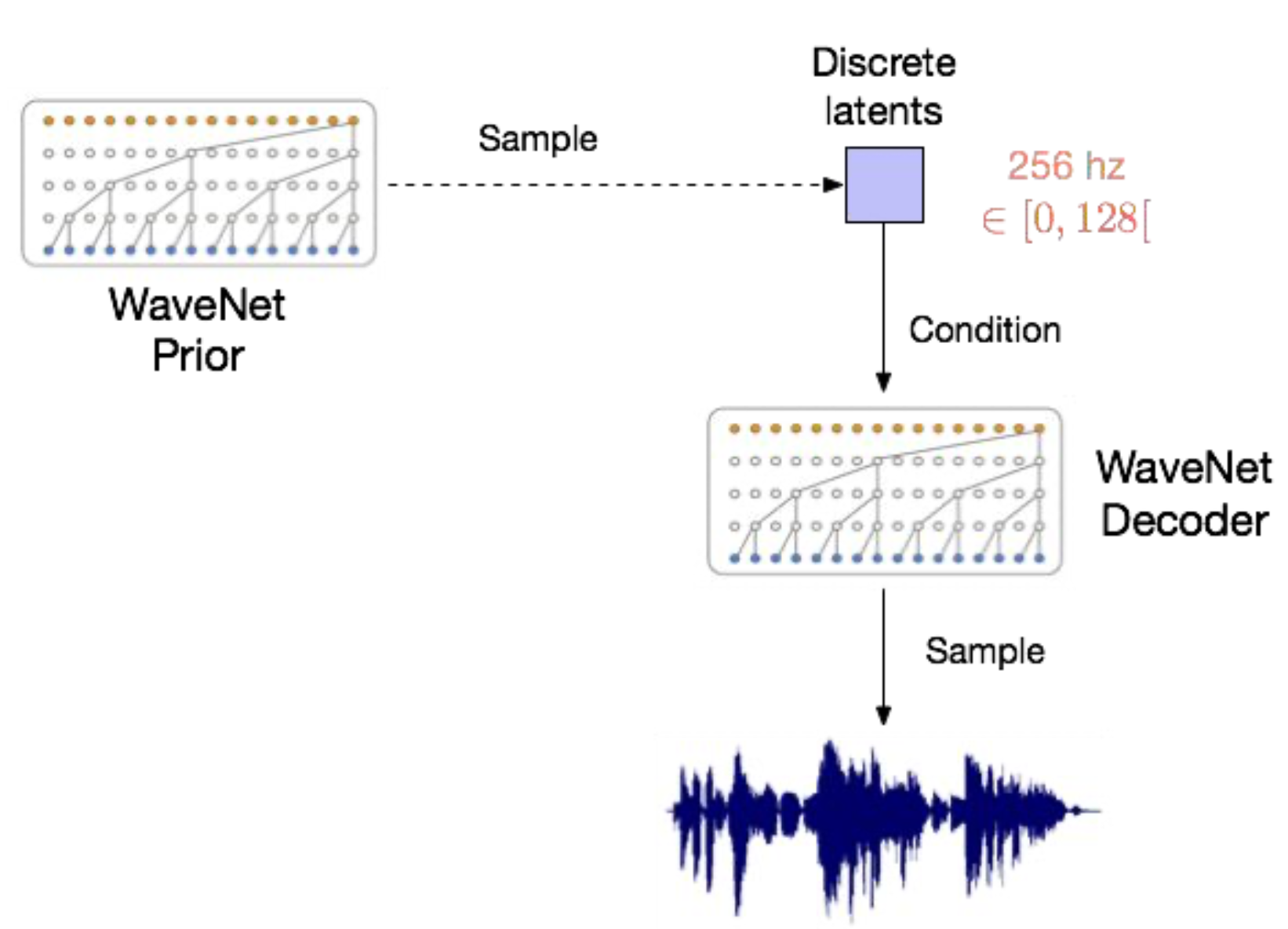 Fig. prior sample Vector들을 Autoregressive하게 만들어서 사용함은 물론이고 Decoder까지 Autoregressive하게 구성했다.
Fig. prior sample Vector들을 Autoregressive하게 만들어서 사용함은 물론이고 Decoder까지 Autoregressive하게 구성했다.
현재 방법론은 학습시에는 prior를 고정하고 학습하고, 추론 시에 prior를 Autoregressive하게 만들어줄 AR Model은 학습 시 생성된 여러 discrete latent vector들을 정답으로 하는 PixelCNN을 따로 학습하는 식으로 이루어지는데, 논문에서는 prior와 VQ-VAE를 동시에 (jointly) 학습하는 것은 future work로 남겨둔다고 하네요.
Training the prior and the VQ-VAE jointly,
which could strengthen our results, is left as future research.
이렇게 여러 Discrete Latent Vector들을 전부 랜덤하게 만드느냐, 아니면 Autoregressive하게 만드느냐는 큰 차이가 있는데요, 아래의 그림은 논문의 그림은 아니고 다른 연구자분이 구현하신 코드의 결과물입니다.
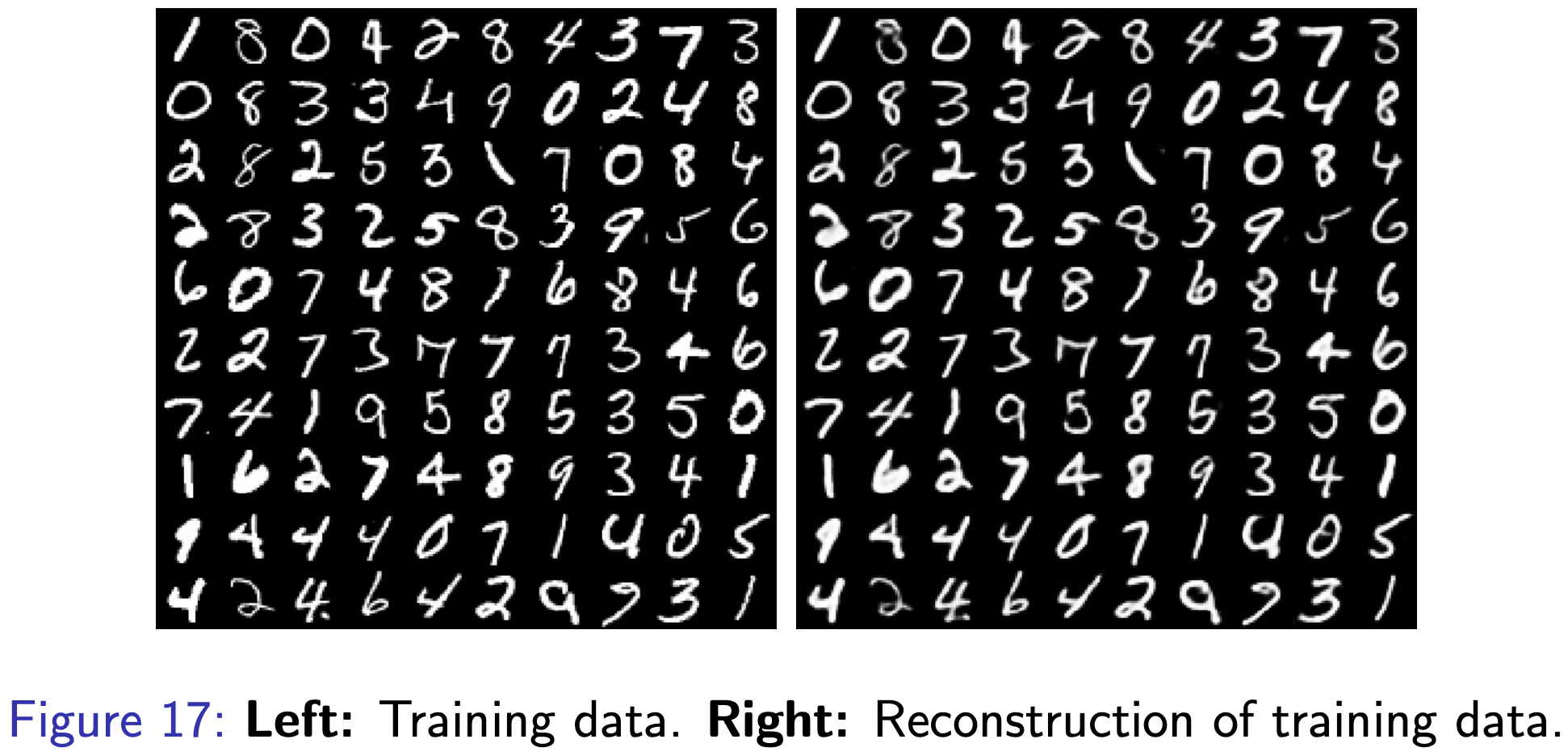 Fig. 학습시 원본 이미지가 어떻게 복원되는지를 보여준다. Discrete Latent Vector를 잘 배운 것을 알 수 있다.
Fig. 학습시 원본 이미지가 어떻게 복원되는지를 보여준다. Discrete Latent Vector를 잘 배운 것을 알 수 있다.
 Fig. 학습 데이터가 아닌 테스트 데이터를 네트워크에 넣어주고, 그렇게 얻은 Discrete Latent Vector를 통해 복원을 해본 결과. 잘 복원되는 걸 알 수 있다.
Fig. 학습 데이터가 아닌 테스트 데이터를 네트워크에 넣어주고, 그렇게 얻은 Discrete Latent Vector를 통해 복원을 해본 결과. 잘 복원되는 걸 알 수 있다.
 Fig. z를 우리가 학습한 코드북으로부터 샘플링 해서 이미지를 생성한 결과. 1024개 벡터를 전부 랜덤으로 생성하는것은 쓰레기 이미지를 만든다는 것을 알 수 있지만, 처음 \(z\)를 샘플링하고 그 뒤로 PixelCNN으로 샘플을 만들어서 구한 prior 시퀀스를 통해 이미지를 생성하면 굉장히 그럴듯한 이미지가 만들어짐을 알 수 있다.
Fig. z를 우리가 학습한 코드북으로부터 샘플링 해서 이미지를 생성한 결과. 1024개 벡터를 전부 랜덤으로 생성하는것은 쓰레기 이미지를 만든다는 것을 알 수 있지만, 처음 \(z\)를 샘플링하고 그 뒤로 PixelCNN으로 샘플을 만들어서 구한 prior 시퀀스를 통해 이미지를 생성하면 굉장히 그럴듯한 이미지가 만들어짐을 알 수 있다.
Other Deep Genrative Models ?
사실 이러한 심층 생성 모델 (Deep Generative Models)은 VAE 말고 다른 것들도 있는데요,
대표적으로 적대적 생성 신경망 (Generative Adversarial Network, GAN)이나 Normalizing Flow Network등이 있습니다.
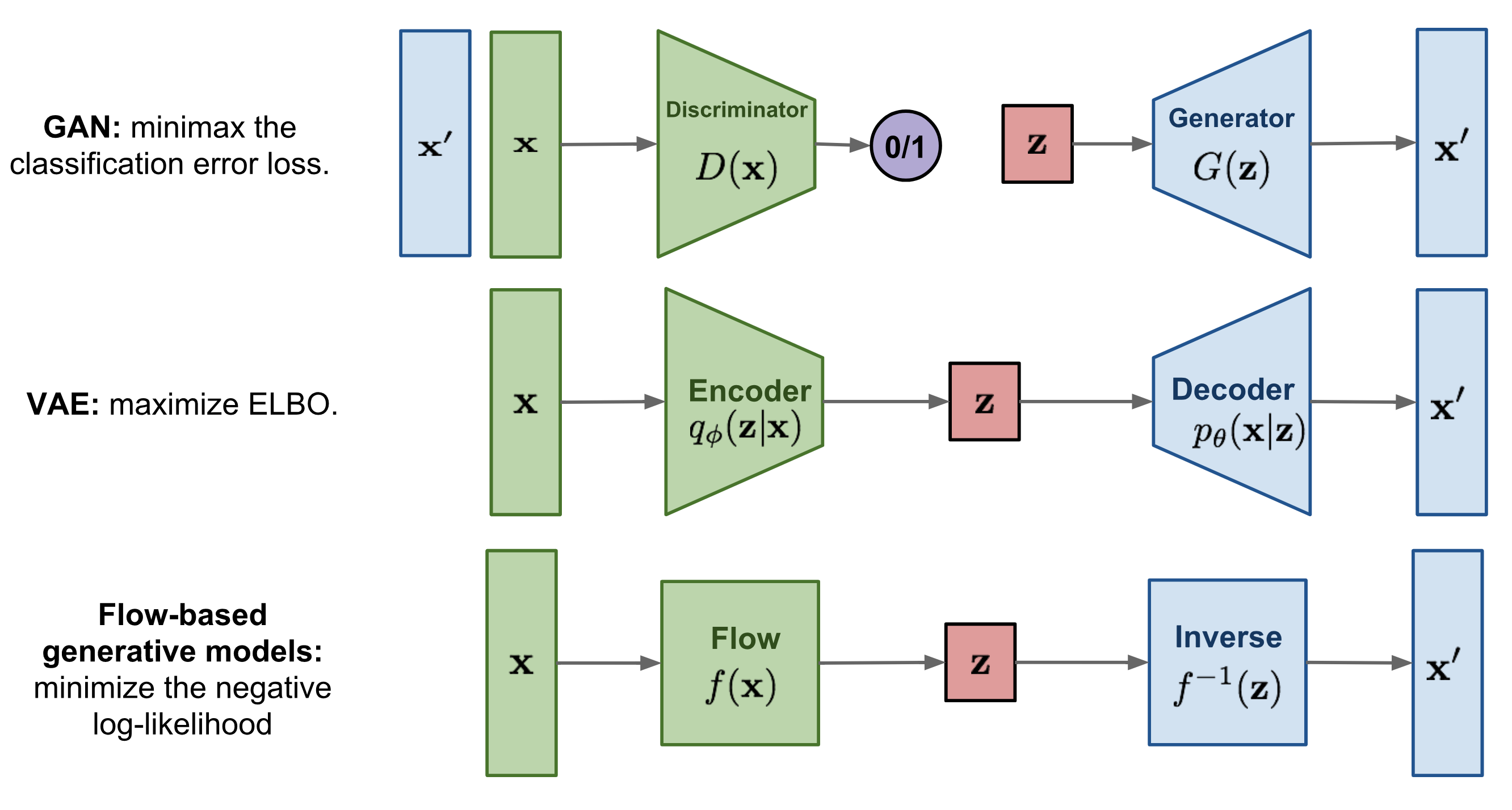 Fig. Three Deep Generative Models
Fig. Three Deep Generative Models
이에 대해서 깊게는 아니고 짧게만 다루고 넘어가도록 해보겠습니다.
Normalizing flow models
Normalizing Flow Model은 VAE와 구조적으로 닮았지만 학습하기는 더 쉬운 생성 모델입니다.
핵심 아이디어는 \(p(x \vert z)\)가 아닌 deterministic decoder을 가지고 있다고 생각 해 보는 겁니다.
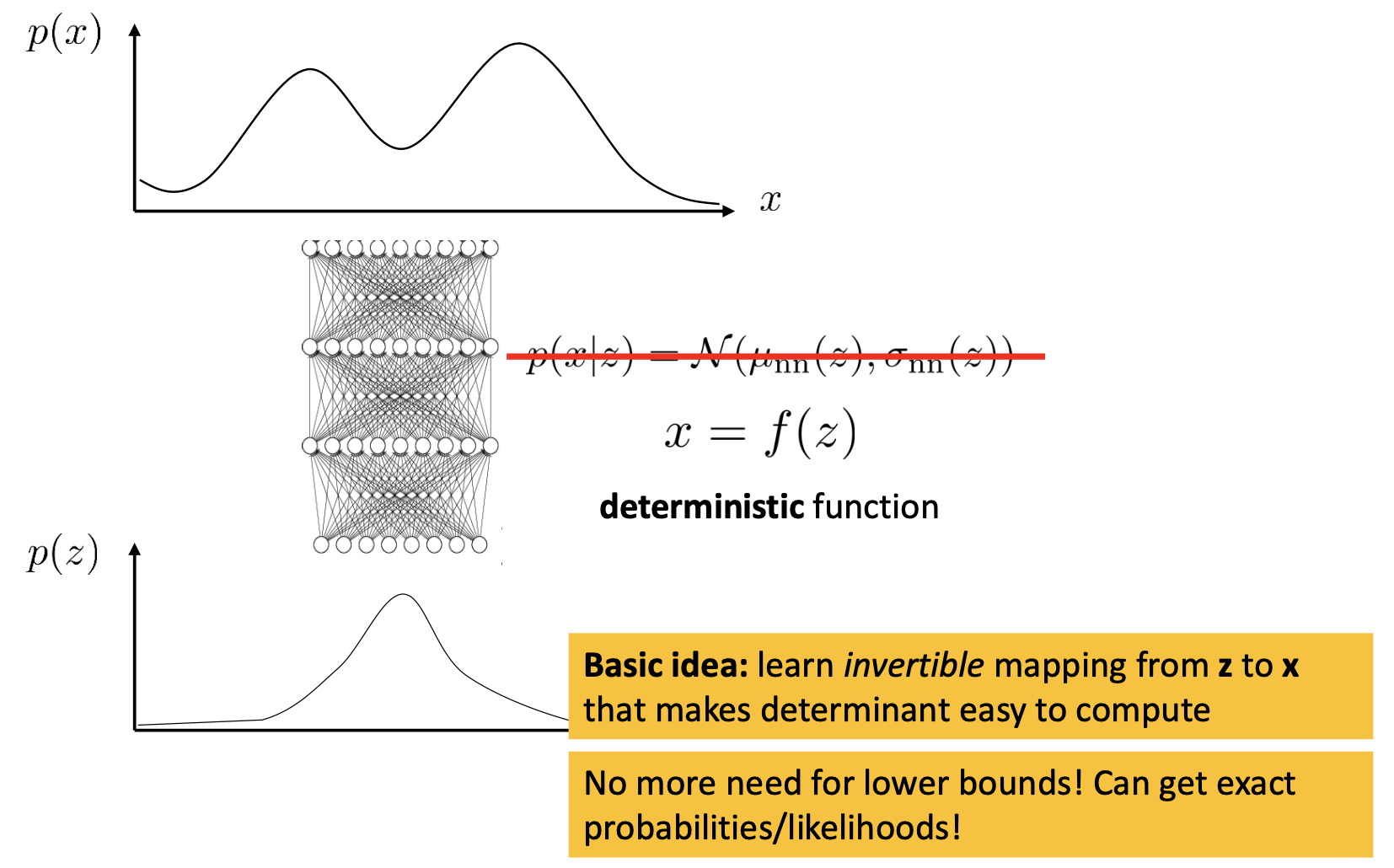 Fig.
Fig.
VAE처럼 \(z\) 분포에서 샘플링을 한 뒤 이를 통해서 디코딩을 하는게 아니라 \(z \rightarrow x\)로 directly 변환해주는 \(x = f(z)\)를 가지고 있는 것이죠.
사실 VAE랑 별로 차이가 없어보이는데요, 이렇게 할 경우 \(p(x)\) 수식이 완전히 바뀌게 됩니다.
- VAE
- Normalizing flow
이 수식이 의미하는 바는 즉, 우리가 \(x \rightarrow z\)인 deterministic한 함수를 알고 있다면, Jacobian 인 \(\frac{df}{dz}\)의 판별식 (Determinant)값을 계산하는 것 만으로도 \(p(z) \rightarrow p(x)\) 처럼 분포를 바꿀 수 있다는 겁니다.
(당연히 여기서 실제 분포인 \(p(z)\)는 복잡한 분포이며, \(p(z)\)는 평균이 0이고 분산이 1인 가우시안 분포처럼 간단한 분포입니다.)
이럴 경우, ELBO를 정해서 이를 최적화할 필요 없이 단박에 likelihood를 얻어낼 수 있다고 합니다.
Normalizing flow model의 Objective를 유도해 보도록 하겠습니다.
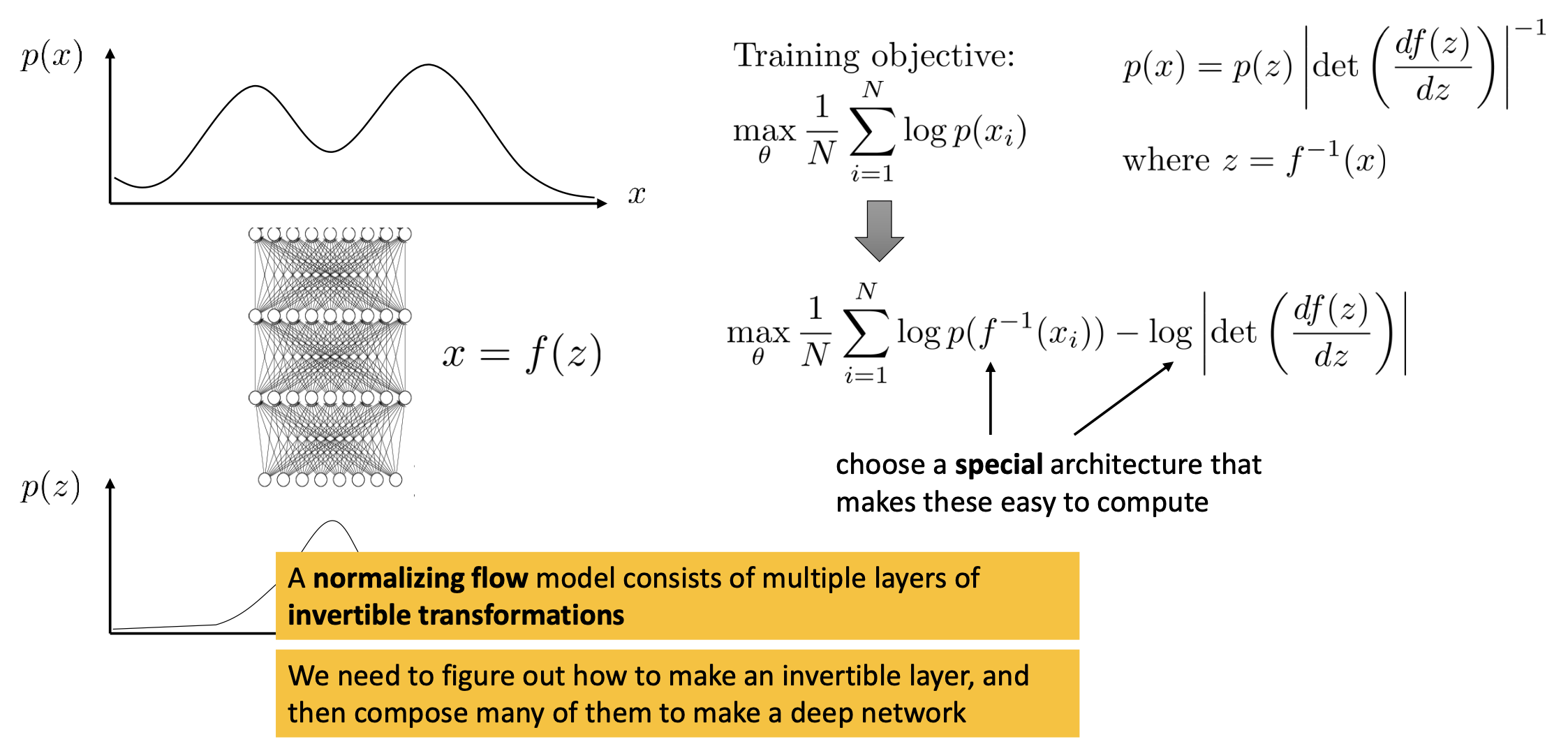 Fig.
Fig.
likelihood를 바로 계산할 것이기 때문에 모든 데이터 샘플에 대해서 log likelihood를 더하면
가 됩니다. 이제 여기에 아래의 관계식을 적용하면
\[\begin{aligned} & p(x) = p(z) \vert det(\frac{df(z)}{dz}) \vert^{-1} & \\ & \text{where } z=f^{-1}(x) & \end{aligned}\]최종적인 Objective는
\[max_{\theta} \frac{1}{N} \sum_{i=1}^{N} [ log p(f^{-1}(x_i)) - log \vert det(\frac{df(z)}{dz}) \vert^{-1} ]\]이 됩니다. 이제 우리가 할 일은 역연산 \(f^{-1}\)과 판별식 계산을 쉽게 할 수 있는 네트워크 \(f\)를 정하기만 하면 됩니다.
예를 들어봅시다. 네트워크 \(f(z)\)가 4층으로 이루어진 네트워크라고 생각해보면,
\[f(z) = f_4 ( f_3 ( f_2 ( f_1 (z) ) ) )\]이제 각 층들을 invertible하게 만들어서 전체 네트워크를 fully-invertible 네트워크로 만들면 됩니다.
Log-determinant는 레이어들이 invertible할 때 간단하게 모든 레이어의 determinant를 계산해서 더하면 되니 일단은 문제가 되지 않는다고 생각하고, 마지막 남은 관문은 네트워크를 invertible하게 만들기만 하면 됩니다.
하지만 이것 까지 다루기에는 글이 너무 길어지기 때문에 (근데 이미 충분히 기네요 …) 자세한 건 다른 포스트에서 다루도록 해보겠습니다.
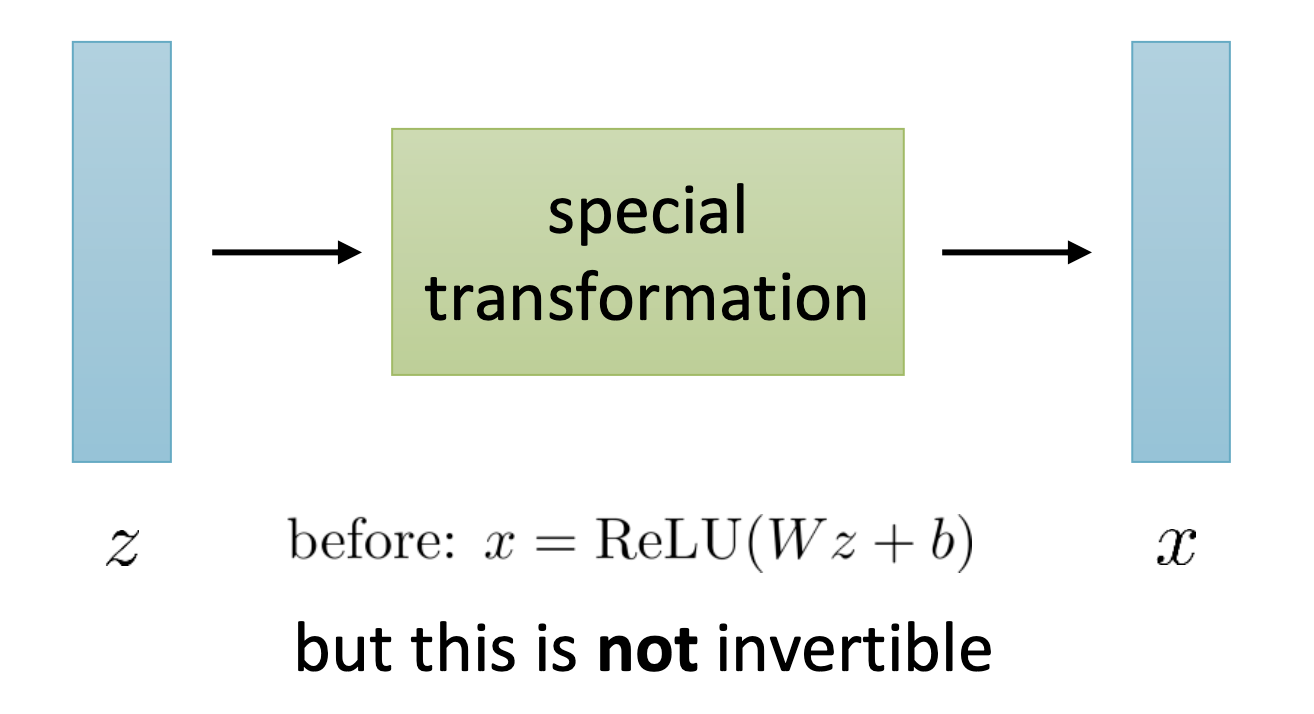 Fig. Non-invertible model
Fig. Non-invertible model
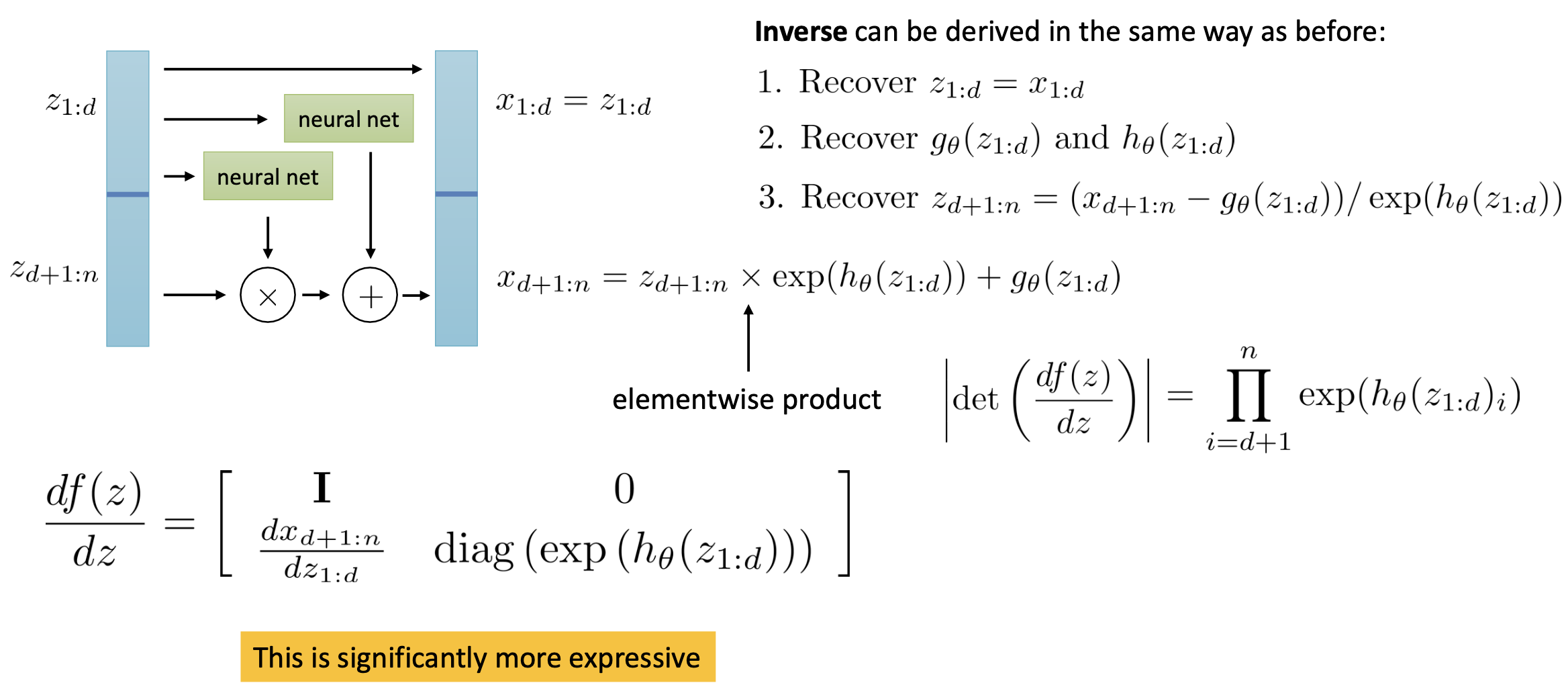 Fig. Invertible model
Fig. Invertible model
마지막으로 덧붙히자면 Normalizing flow는 아래와 같은 장단점이 있습니다.
- Pros
- can get exact probabilities/likelihoods
- no need for lower bounds
- conceptually simpler (perhaps)
- Cons
- requires special architecture
zmust have same dimensionality asx
Generative Adversarial Networks (GAN)
적대적 생성 신경망 (Generative Adversarial Networks, GAN)은 정해진 학습 데이터들에 대해서 \(z\)가 어떤 이미지로 매핑될 지를 log-likelihood를 최대화 하는 방향으로 (ELBO를 최대화) 지도 학습 하는 VAE 달리, 학습 데이터들 뿐만 아니라 만들어진 모든 진짜같은 이미지들에 대해서 두 네트워크가 경쟁하듯 학습되는 method 입니다.
딱히 뚜렷한 Objective가 없는 (not a clear objective function to optimize) 방법론 이라고 하기도 하는데요, (Bengio’s reply for GAN](https://www.quora.com/What-are-the-pros-and-cons-of-Generative-Adversarial-Networks-vs-Variational-Autoencoders))
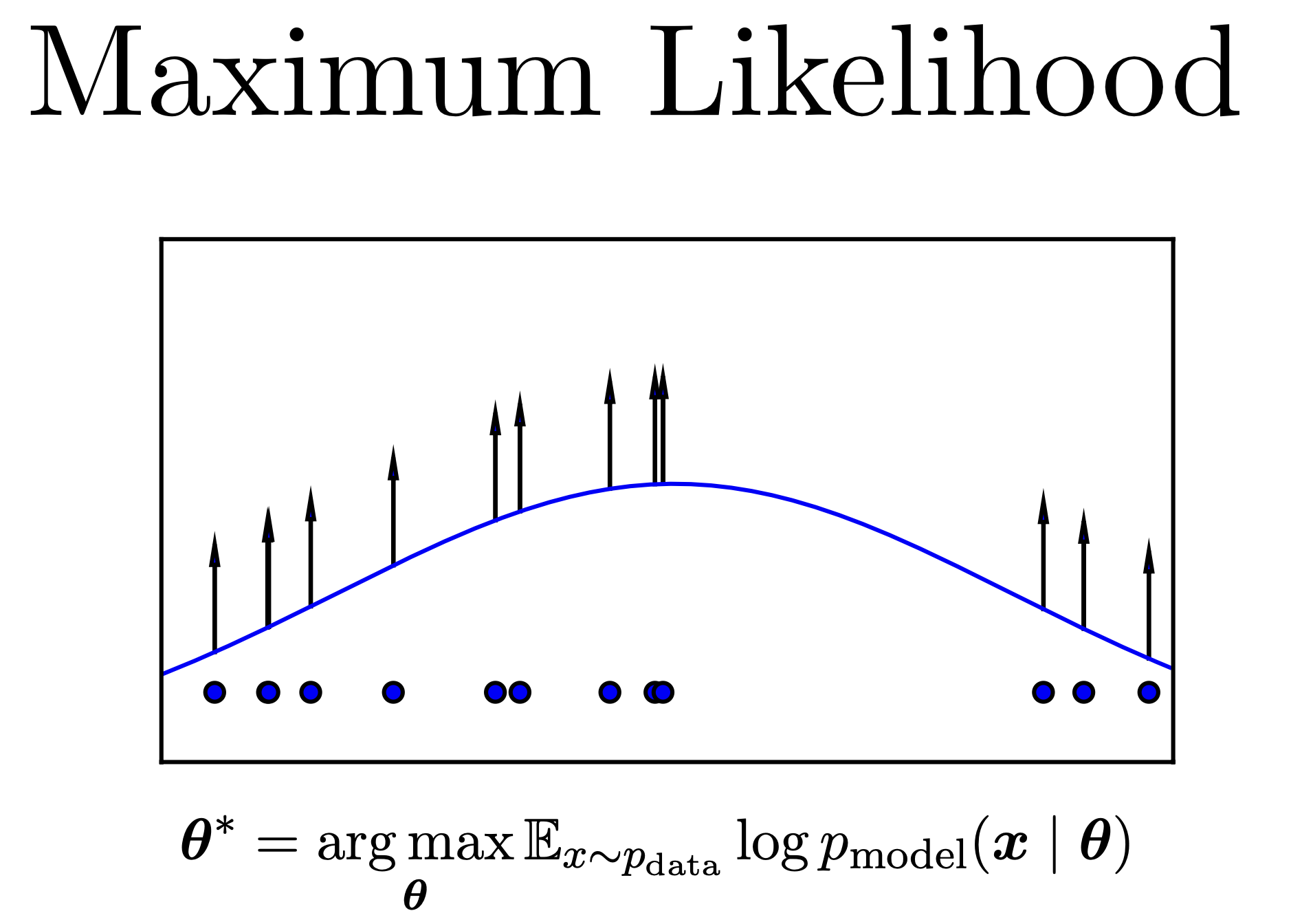 Fig. Maximum likelihood 문제를 푸는 VAE
Fig. Maximum likelihood 문제를 푸는 VAE
VAE는 우리가 모델링할 분포가 어떻게 생겼는지 명시 (Explicit) 해주고 이 likelihood 를 최대화 하는 데 반해,
GAN 은 이런것이 없이 학습하지만 결국 암시적 (Implicit)으로 이것이 학습은 되는 방법론이라는 말을 하는데 Bengio는 이 말을 하는 것 같습니다.
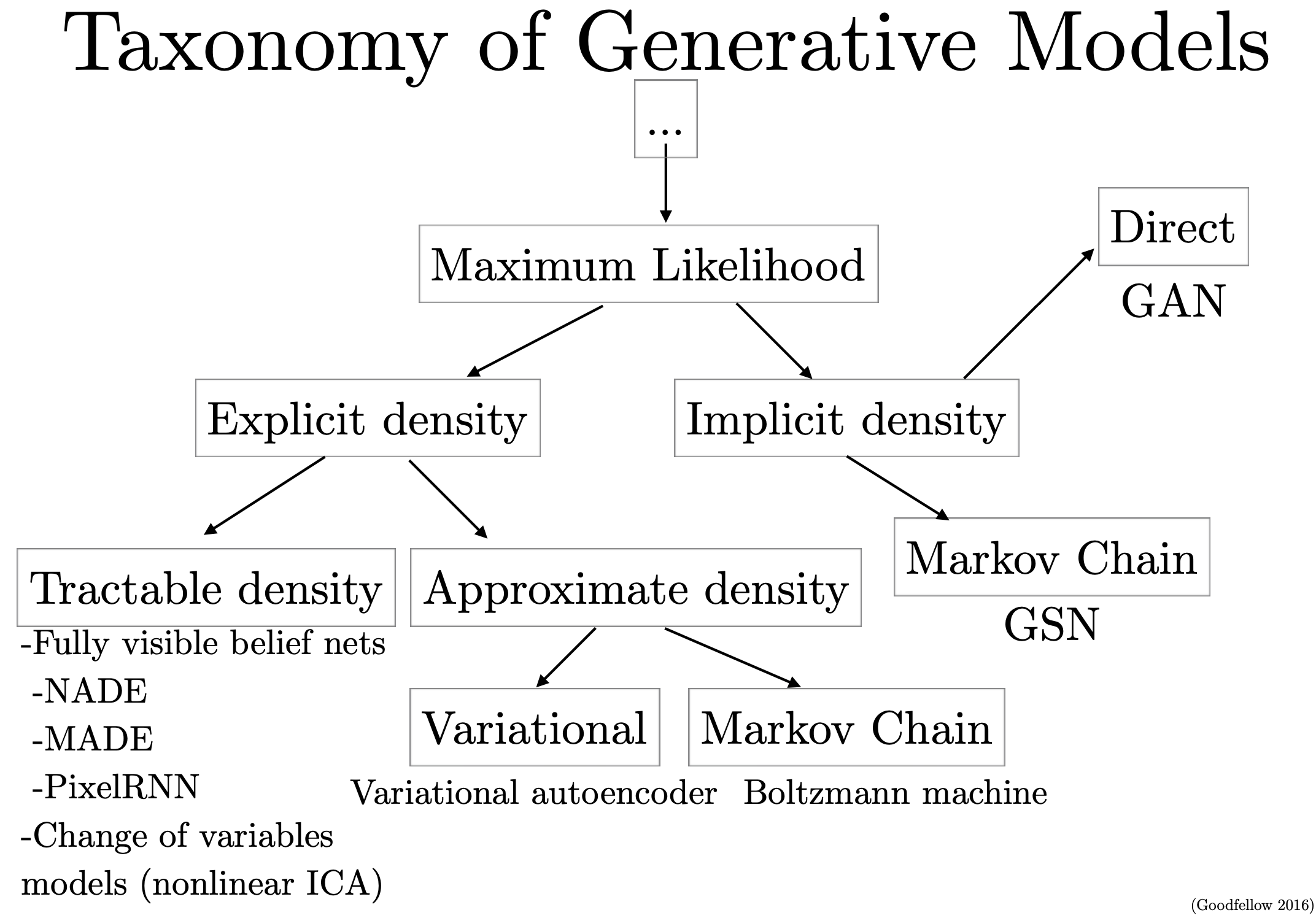 Fig. 분포를 가정하는 (loss가 정해짐) 방법론인 VAE와 그렇지 않은 GAN
Fig. 분포를 가정하는 (loss가 정해짐) 방법론인 VAE와 그렇지 않은 GAN
GAN의 기본적인 아이디어는 \(z\)로부터 이미지를 만들어내는 생성자 (Generator), 그리고 학습 데이터셋에 있는 이미지는 True라고 구분하고 \(z\)로부터 만들어진 이미지는 False 라고 구분하는 판별자 (Discriminator)라고
하는 네트워크를 두 가지 정의하고
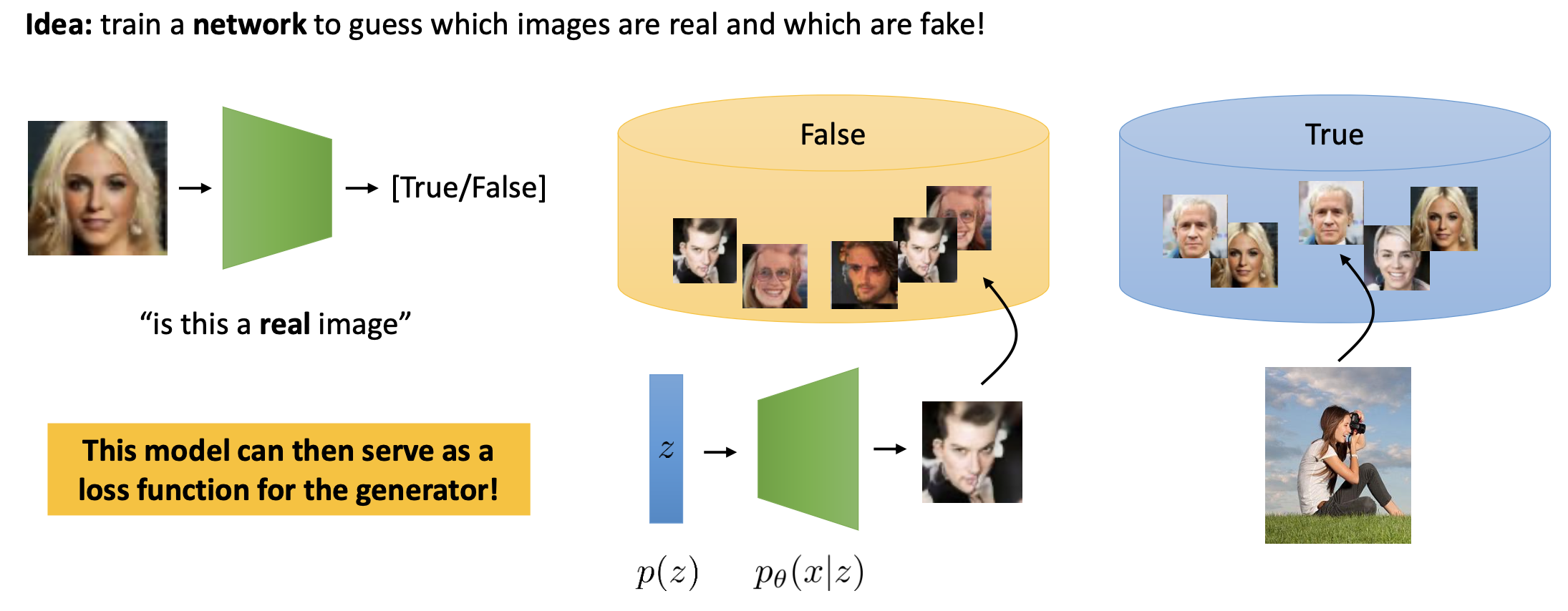 Fig. GAN의 아이디어
Fig. GAN의 아이디어
이 두 가지 네트워크를 아래와 같은 Objective로 학습합니다.

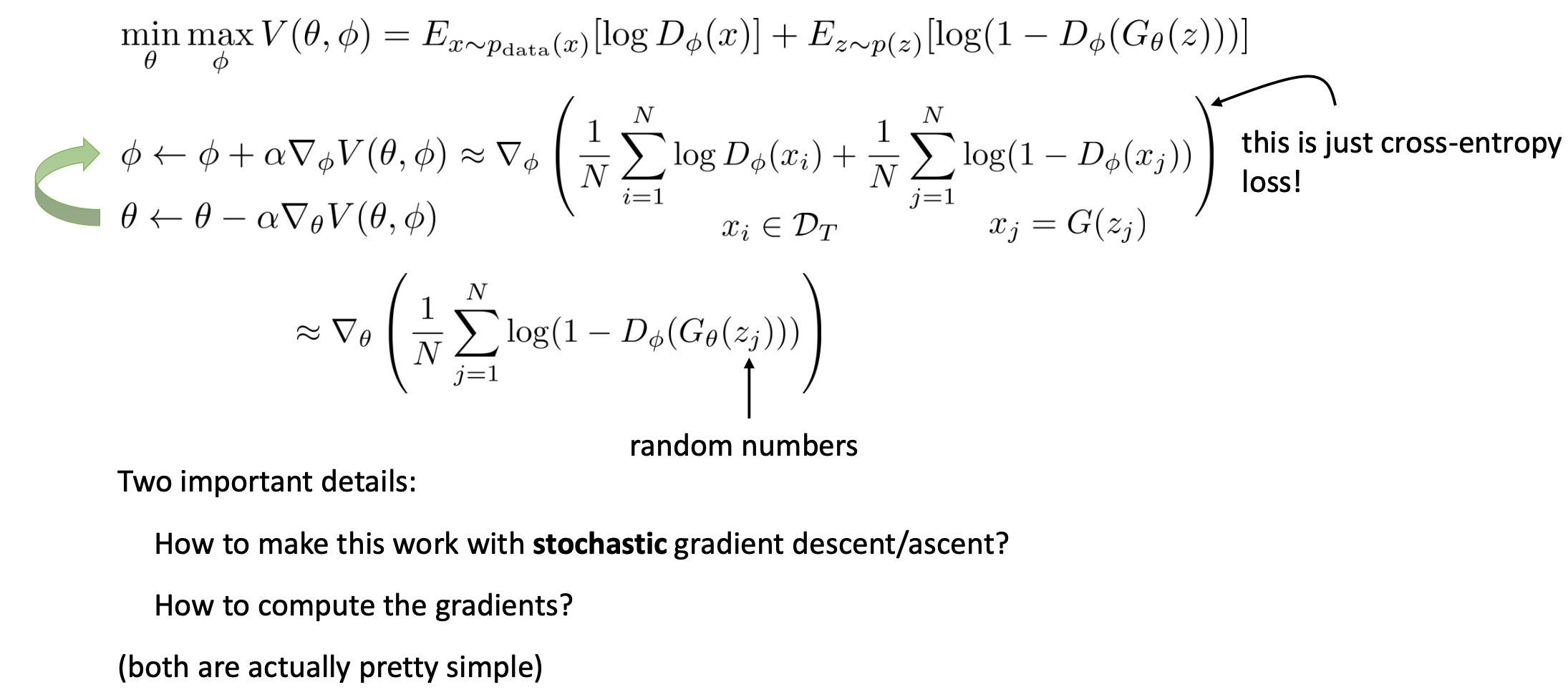 Fig. GAN이 생성 모델링 문제를 푸는 Flow.
Fig. GAN이 생성 모델링 문제를 푸는 Flow.
GAN에는 왜 이것이 잘 되는지?, 어떻게 최적화가 되는지? 등에 대해서 다른 포스트에서 자세히 다뤄보도록 하려고 합니다.
마지막으로 GAN과 VAE의 차이점 혹은 장단점은 무엇이 있을까 ? 라는 글에 세계적인 ML 분야 석학이자 GAN을 제안한 Ian Goodfellow의 Advisor인 Yoshua Bengio의 답변을 끝으로 post를 마무리 하도록 하겠습니다.
Q. What are the pros and cons of Generative Adversarial Networks vs Variational Autoencoders?
A.An advantage for VAEs (Variational AutoEncoders) is that there is a clear and recognized way
to evaluate the quality of the model (log-likelihood, either estimated by importance sampling or lower-bounded).
Right now it’s not clear how to compare two GANs (Generative Adversarial Networks)
or compare a GAN and other generative models except by visualizing samples.
A disadvantage of VAEs is that, because of the injected noise and imperfect reconstruction,
and with the standard decoder (with factorized output distribution),
the generated samples are much more blurred than those coming from GANs.
The fact that VAEs basically optimize likelihood
while GANs optimize something else can be viewed both as an advantage or a disadvantage for either one.
Maximizing likelihood yields an estimated density that always bleeds probability mass away from the estimated data manifold.
GANs can be happy with a very sharp estimated density function even if it does not perfectly coincide with the data density
(i.e. some training examples may come close to the generated images
but might still have nearly zero probability under the generator, which would be infinitely bad in terms of likelihood).
GANs tend to be much more finicky to train than VAEs,
not to mention that we do not have a clear objective function to optimize,
but they tend to yield nicer images.
References
- Papers
- Lectures
- CS W182 / 282A at UC Berkeley - Designing, Visualizing and Understanding Deep Neural Networks
- Deep Generative Model Lecture from Stefano Ermon Lab
- Latent Variable Models (VAE) – CS294-158-SP20 Deep Unsupervised Learning – UC Berkeley from Pieter Abbeel
- ‘오토 인코더의 모든 것 (1~3)’ from Hwalseok Lee
- VAE말고 Auto-encoding variational bayes를 알아보자
- Other
- Blogs
- Latent variable models, part 1 Gaussian mixture models and the EM algorithm from Martin Krasser
- Latent variable models, part 2 Stochastic variational inference and variational autoencoders from Martin Krasser
- A Beginner’s Guide to Variational Methods: Mean-Field Approximation from Eric Jang
- from AutoEncoder to beta VAE by lillog
- Tutorial #5 variational autoencoders from BorealisAI
- EM Algorithm